Куб Гильберта - Hilbert cube
В математика, то Куб Гильберта, названный в честь Дэвид Гильберт, это топологическое пространство это дает поучительный пример некоторых идей в топология. Более того, многие интересные топологические пространства могут быть вложены в гильбертовый куб; то есть можно рассматривать как подпространства гильбертова куба (см. ниже).
Определение
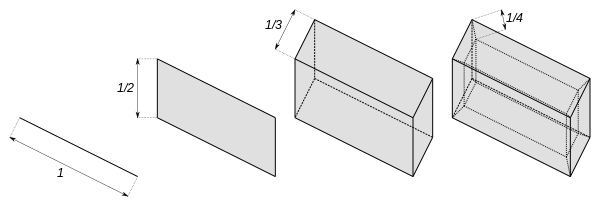
Куб Гильберта лучше всего определить как топологический продукт из интервалы [0, 1/п] за п = 1, 2, 3, 4, ... То есть это кубовид из счетно бесконечный измерение, где длины ребер в каждом ортогональном направлении образуют последовательность .
Куб Гильберта гомеоморфный к продукту счетно бесконечно много копий единичный интервал [0, 1]. Другими словами, он топологически неотличим от единичный куб счетно бесконечного измерения.
Если точка в кубе Гильберта задана последовательностью с , то гомеоморфизм бесконечномерного единичного куба задается формулой .
Гильбертовый куб как метрическое пространство
Иногда удобно рассматривать куб Гильберта как метрическое пространство, действительно как конкретное подмножество разделимых Гильбертово пространство (то есть гильбертово пространство со счетно бесконечным гильбертовым базисом). Для этих целей лучше не думать о нем как о произведении копий [0,1], а вместо этого как
- [0,1] × [0,1/2] × [0,1/3] × ···;
как указано выше, для топологических свойств это не имеет значения, то есть элемент куба Гильберта является бесконечная последовательность
- (Иксп)
это удовлетворяет
- 0 ≤ Иксп ≤ 1/п.
Любая такая последовательность принадлежит гильбертову пространству ℓ2, поэтому куб Гильберта наследует оттуда метрику. Можно показать, что топология, индуцированная метрикой, такая же, как топология топология продукта в приведенном выше определении.
Характеристики
Как продукт компактный Хаусдорфовы пространства, гильбертовый куб сам является компактным хаусдорфовым пространством в результате Теорема Тихонова Компактность гильбертова куба также может быть доказана без аксиомы выбора путем построения непрерывной функции из обычных Кантор набор на куб Гильберта.
В ℓ2, ни одна точка не имеет компактного район (таким образом, ℓ2 не является локально компактный ). Можно было ожидать, что все компактные подмножества2 конечномерны. Куб Гильберта показывает, что это не так. Но куб Гильберта не может быть окрестностью любой точки. п потому что его сторона становится все меньше и меньше в каждом измерении, так что открытый мяч вокруг п любого фиксированного радиуса е > 0 должен выходить за пределы куба в каком-то измерении.
Любое бесконечномерное выпуклое компактное подмножество гомеоморфно кубу Гильберта. Куб Гильберта - это выпуклое множество, длина которого равна всему пространству, но внутреннее пространство пусто. Такая ситуация невозможна в конечных размерах. Касательный конус к кубу в нулевом векторе - это все пространство.
Каждое подмножество гильбертова куба наследует от гильбертова свойства метризуемости (и, следовательно, Т4 ) и второй счетный. Более интересно, что верно и обратное: каждый второй счетный Т4 пространство гомеоморфно подмножеству гильбертова куба.
Каждый Gδ-подмножество куба Гильберта является Польское пространство, топологическое пространство, гомеоморфное сепарабельному и полному метрическому пространству. Наоборот, каждое польское пространство гомеоморфно пространству граммδ-подмножество куба Гильберта.[1]
Примечания
- ^ Шривастава, стр.55
Рекомендации
- Шривастава, Шаши Мохан (1998). Курс борелевских множеств. Тексты для выпускников по математике. Springer-Verlag. ISBN 978-0-387-98412-4. Получено 2008-12-04.
- "Die Homoiomorphie der kompakten konvexen Mengen im Hilbertschen Raum" [Гомоморфизм компактных выпуклых множеств в гильбертовом пространстве] (на немецком языке). EUDML. Архивировано из оригинал на 2020-03-02.
дальнейшее чтение
- Стин, Линн Артур; Зеебах, Дж. Артур мл. (1995) [1978]. Контрпримеры в топологии (Дувр переиздание 1978 г.). Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-0-486-68735-3. МИСТЕР 0507446.





