Список метаэвристики на основе метафор - List of metaphor-based metaheuristics

Это хронологически упорядоченный список основанных на метафорах метаэвристика и рой интеллект алгоритмы.

Алгоритмы

Этот список неполный; вы можете помочь добавление недостающих предметов с надежные источники.

Имитация отжига (Киркпатрик и др., 1983)

Основная статья: Имитация отжига

Имитационный отжиг (SA) - это вероятностный техника, вдохновленная методом термообработки в металлургия. Он часто используется, когда область поиска дискретна (например, все туры, которые посещают заданный набор городов). Для задач, где нахождение точного глобального оптимума менее важно, чем нахождение приемлемого локального оптимума за фиксированный промежуток времени, имитация отжига может быть предпочтительнее альтернатив, таких как градиентный спуск.

При моделировании отжига медленное охлаждение интерпретируется как медленное уменьшение вероятности принятия худших решений по мере изучения пространства решений. Принятие худших решений является фундаментальным свойством метаэвристики, поскольку оно позволяет осуществлять более обширный поиск оптимального решения.

Оптимизация колонии муравьев (Дориго, 1992)

Основная статья: Алгоритмы оптимизации муравьиной колонии

Алгоритм оптимизации муравьиной колонии (ACO) - это вероятностный метод решения вычислительных задач, который можно свести к поиску хороших путей через графики. Первоначально предложено Марко Дориго в 1992 г. защитил кандидатскую диссертацию,^[1][2] первый алгоритм был нацелен на поиск оптимального пути в графе на основе поведения муравьи ищет путь между своими колония и источник пищи. Первоначальная идея с тех пор изменилась, чтобы решить более широкий класс численных задач, и в результате возникло несколько проблем, основанных на различных аспектах поведения муравьев. В более широком смысле ACO выполняет поиск на основе модели^[3] и имеет некоторые сходства с Оценка алгоритмов распределения.

Оптимизация роя частиц (Кеннеди и Эберхарт, 1995)

Основная статья: Оптимизация роя частиц

Оптимизация роя частиц (PSO) - это вычислительный метод, который оптимизирует проблема итеративно пытаясь улучшить возможное решение в отношении данной меры качества. Он решает проблему, имея множество вариантов решения, здесь названных частицы, и перемещая эти частицы в поисковое пространство в соответствии с простым математические формулы над частицей позиция и скорость. На движение каждой частицы влияет ее местное наиболее известное положение, но оно также направляется к наиболее известным позициям в пространстве поиска, которые обновляются по мере того, как другие частицы находят лучшие позиции. Ожидается, что это подтолкнет рой к лучшим решениям.

PSO изначально приписывается Кеннеди, Эберхарт и Ши^[4][5] и сначала был предназначен для моделирование социальное поведение,^[6] как стилизованное изображение движения организмов в птице стадо или косяк рыб. Алгоритм был упрощен, и было замечено, что выполняется оптимизация. Книга Кеннеди и Эберхарта^[7] описывает многие философские аспекты PSO и рой интеллект. Обширный обзор приложений PSO выполнен Поли.^[8][9] Недавно Боньяди и Михалевич опубликовали подробный обзор теоретических и экспериментальных работ по PSO.^[10]

Поиск гармонии (Джем, Ким и Логанатан, 2001)

Поиск гармонии - это подражание явлению метаэвристический представленный в 2001 году Зонг У Гем, Джунг Хун Ким и Г. В. Логанатаном.^[11] Поиск гармонии вдохновлен процессом импровизации джазовых музыкантов. В одной статье утверждается, что поиск гармонии - это частный случай Стратегии развития алгоритм. ^[12] Однако в недавней статье утверждается, что структура стратегий эволюции отличается от структуры поиска гармонии. ^[13] Также был предоставлен программный код, показывающий, как HS решает судоку.^[14]

Поиск гармонии (HS) - это относительно простой, но очень эффективный эволюционный алгоритм. В алгоритме HS случайным образом генерируется набор возможных решений (называемый памятью гармонии). Новое решение генерируется с использованием всех решений в памяти Harmony (а не только двух, как в GA), и если это новое решение лучше, чем худшее решение в памяти Harmony, худшее решение заменяется этим новым решением. Хотя HS является относительно новым метаэвристическим алгоритмом, его эффективность и преимущества были продемонстрированы в различных приложениях, таких как проектирование муниципальных сетей водоснабжения,^[15] структурный дизайн,^[16] маршрутизация трафика,^[17] проблема диспетчеризации нагрузки в электротехнике,^[18] многокритериальная оптимизация,^[19] проблемы со списком,^[20] кластеризация^[21] классификация и выбор признаков^[22][23] назвать несколько. Подробный обзор приложений HS можно найти в ^[24][25] и приложения HS для интеллектуального анализа данных можно найти в ^[26].

Алгоритм искусственной пчелиной семьи (Карабога 2005)

Основная статья: Алгоритм искусственной пчелиной семьи

Алгоритм искусственной пчелиной семьи - это метаэвристический алгоритм, представленный Карабогой в 2005 году.^[27] и имитирует кормление медоносных пчел. Алгоритм ABC состоит из трех этапов: используемая пчела, пчела-наблюдатель и пчела-разведчик. В фазах использованной пчелы и фазы пчелы-наблюдателя пчелы используют источники путем локального поиска в окрестностях решений, выбранных на основе детерминированного выбора в фазе используемой пчелы и вероятностный отбор в фазе пчелы-наблюдателя. На этапе разведки пчел, который является аналогом отказа от истощенных источников пищи в процессе поиска пищи, решения, которые больше не приносят пользы для прогресса поиска, отбрасываются, и вместо них вставляются новые решения для исследования новых регионов в пространстве поиска. Алгоритм обладает хорошо сбалансированной способностью к исследованию и эксплуатации.

Алгоритм пчел (Pham 2005)

Основная статья: Алгоритм пчел

Алгоритм пчел в его базовой формулировке был создан Фамом и его сотрудниками в 2005 году.^[28] и в последующие годы доработан.^[29] Создано по образцу кормового поведения медоносные пчелы, алгоритм сочетает глобальный исследовательский поиск с локальным эксплуатационным поиском. Небольшое количество искусственных пчел (разведчиков) случайным образом исследует пространство решений (среду) для решений высокой пригодности (высокодоходные источники пищи), в то время как большая часть населения ищет (собирает урожай) окрестности наиболее подходящих решений в поисках оптимальной пригодности . Детерминистическая процедура приема на работу, которая имитирует виляющий танец биологических пчел используется для передачи результатов разведчиков фуражирам и распределения собирателей в зависимости от пригодности районов, выбранных для местного поиска. Как только поиск в окрестности решения прекращается, считается, что локальный оптимум пригодности найден, и сайт покидают. Таким образом, алгоритм пчел одновременно выполняет поиск наиболее перспективных областей пространства решений, в то же время непрерывно производя отбор проб в поисках новых благоприятных областей.

Оптимизация роя светлячков (Кришнананд и Гхос, 2005)

Оптимизация роя светлячков - это рой интеллект оптимизация алгоритм разработан на основе поведения светлячки (также известные как светлячки или молнии). Алгоритм GSO был разработан и представлен К. Кришнананд и Дебасиш Гхош в 2005 г. в Лаборатории систем наведения, контроля и принятия решений Департамента аэрокосмической техники Индийский институт науки, Бангалор, Индия.^[30]

Образец поведения светлячков, который используется для этого алгоритма, представляет собой очевидную способность светлячков изменять интенсивность излучения люциферина и, таким образом, кажется, что они светятся с разной интенсивностью.

1. Алгоритм GSO заставляет агентов светиться с интенсивностью, приблизительно пропорциональной значению оптимизируемой функции. Предполагается, что светлячки большей интенсивности привлекают светлячков меньшей интенсивности.
2. Вторая важная часть алгоритма включает динамический диапазон принятия решений, с помощью которого эффект удаленных светлячков не учитывается, когда светлячок имеет достаточное количество соседей или диапазон выходит за пределы диапазона восприятия светлячков.

Часть 2 алгоритма отличает его от других эволюционная мультимодальная оптимизация алгоритмы. Именно этот шаг позволяет светлячку рои для автоматического разделения на подгруппы, которые затем могут сходиться к нескольким локальным оптимумам одновременно. Это свойство алгоритма позволяет использовать его для определения нескольких пиков мультимодальной функции и делает его частью эволюционного семейства алгоритмов мультимодальной оптимизации.

Алгоритм перетасованного лягушачьего прыжка (Eusuff, Lansey & Pasha, 2006)

Перемешанный алгоритм прыжка лягушки - это алгоритм оптимизации, используемый в искусственный интеллект.^[31] Это сравнимо с генетический алгоритм.

Оптимизация роя кошек (Чу, Цай и Пан, 2006)

Алгоритм оптимизации кошачьего роя, который решает проблемы оптимизации и основан на поведении кошек.^[32] Он похож на другие алгоритмы оптимизации роя, такие как алгоритмы оптимизации муравьиной колонии или оптимизации роя частиц. Поиск и отслеживание, два распространенных поведения кошек, составляют две подмодели алгоритма. Режим поиска основан на поведении отдыхающей кошки, которая ищет, куда двигаться дальше. В режиме поиска он выбирает несколько точек-кандидатов, а затем выбирает одну для случайного перемещения, увеличивая вероятность выбора точек с более высоким значением пригодности. Режим отслеживания вдохновлен кошкой, выслеживающей цель. В этом режиме кошка будет пытаться перейти в позицию с наилучшим показателем пригодности. Кошки будут продолжать движение в режиме поиска и отслеживания, пока не будет выполнено условие завершения.

Империалистический конкурентный алгоритм (Аташпаз-Гаргари и Лукас, 2007)

Основная статья: Империалистический конкурентный алгоритм

Империалистический конкурентный алгоритм - это вычислительный метод, который используется для решения проблемы оптимизации разных типов.^[33][34] Как и большинство методов в области эволюционные вычисления, ICA не нуждается в градиенте функции в процессе оптимизации. С определенной точки зрения, ICA можно рассматривать как социальный аналог генетические алгоритмы (ГА). ICA - это математическая модель и компьютерное моделирование человеческого социальная эволюция, а ГА основаны на биологическая эволюция видов.

Этот алгоритм начинается с генерации набора случайных возможных решений в пространстве поиска задачи оптимизации. Сгенерированные случайные точки называются начальными Страны. Страны в этом алгоритме являются аналогом Хромосомаs в GA и Частицыс в Оптимизация роя частиц (PSO) и представляет собой массив значений варианта решения задачи оптимизации. В функция стоимости Задача оптимизации определяет мощь каждой страны. В зависимости от их мощности некоторые из лучших исходных стран (страны с наименьшим значением функции затрат) становятся Империалисты и начать брать под свой контроль другие страны (называемые колонии) и образуют начальную Империи.^[33]

Два основных оператора этого алгоритма: Ассимиляция и Революция. Ассимиляция приближает колонии каждой империи к империалистическому государству в пространстве социально-политических характеристик (пространство поиска оптимизации). Революция приводит к внезапным случайным изменениям в положении некоторых стран в поисковом пространстве. Во время ассимиляции и революции колония может занять лучшее положение и получить шанс взять под контроль всю империю и заменить текущее империалистическое государство империи.^[35]

Империалистическое соревнование это другая часть этого алгоритма. Все империи пытаются выиграть эту игру и завладеть колониями других империй. На каждом этапе алгоритма, в зависимости от своей мощи, все империи имеют шанс взять под контроль одну или несколько колоний самой слабой империи.^[33]

Алгоритм продолжается с упомянутых шагов (Ассимиляция, Революция, Конкуренция) до тех пор, пока не будет выполнено условие остановки.

Вышеуказанные шаги можно резюмировать следующим образом: псевдокод.^[34][35]

0) Определите целевую функцию: ${\displaystyle f(\mathbf {x} ),\quad \mathbf {x} =(x_{1},x_{2},\dots ,x_{d});\,}$1) Инициализация алгоритма. Сгенерируйте какое-нибудь случайное решение в области поиска и создайте первоначальные империи. 2) Ассимиляция: колонии движутся к империалистическим государствам в разных направлениях. 3) Революция: в характеристиках некоторых стран происходят случайные изменения. 4) Обмен позициями между колонией и империалистом. Колония с лучшим положением, чем империалистическая, имеет шанс взять под свой контроль империю, заменив существующего империалистического. 5) Империалистическое соревнование: все империалисты соревнуются за владение колониями друг друга. 6) Устранение бессильных империй. Слабые империи постепенно теряют свою мощь и, наконец, будут уничтожены. 7) Если условие останова выполнено, остановитесь, если нет, перейдите к 2.8) Конец

Динамика формирования рек (Rabanal, Rodríguez & Rubio 2007)

Динамика формирования рек основана на имитации того, как вода образует реки, размывая землю и осаждая отложения (капли действуют как рой). После того, как капли преобразуют ландшафт, увеличивая / уменьшая высоту мест, решения даются в виде путей уменьшения высоты. Строятся убывающие градиенты, и за этими градиентами следуют последующие падения, чтобы составить новые градиенты и усилить лучшие. Этот метод эвристической оптимизации был впервые представлен в 2007 году Rabanal et al.^[36] Применимость RFD к другим NP-полным задачам была изучена.^[37] и алгоритм был применен к таким областям, как маршрутизация^[38] и робот-навигация.^[39] Основные области применения RFD можно найти в подробном обзоре.^[40]

Интеллектуальный алгоритм капель воды (Шах-Хоссейни 2007)

Интеллектуальный алгоритм капель воды содержит несколько основных элементов естественных капель воды, а также действий и реакций, которые происходят между дном реки и текущими каплями воды. IWD был впервые представлен для задача коммивояжера в 2007.^[41]

Практически каждый алгоритм IWD состоит из двух частей: графа, который играет роль распределенной памяти, на которой сохраняются почвы разных краев, и подвижной части алгоритма IWD, которая представляет собой несколько интеллектуальных капель воды. Эти интеллектуальные капли воды (IWD) одновременно соревнуются и сотрудничают, чтобы найти лучшие решения, и, изменяя почвы на графике, пути к лучшим решениям становятся более доступными. Упоминается, что для работы алгоритмов на основе IWD требуется как минимум два IWD.

Алгоритм IWD имеет два типа параметров: статические и динамические параметры. Статические параметры постоянны в процессе работы алгоритма IWD. Динамические параметры повторно инициализируются после каждой итерации алгоритма IWD. Псевдокод алгоритма на основе IWD может быть определен в восемь шагов:

1) Инициализация статических параметров

а) Представление задачи в виде графа

б) Установка значений для статических параметров

2) Инициализация динамических параметров: грунт и скорость IWD

3) Распределение IWD на графе задачи

4) Построение решения с помощью IWD вместе с обновлением почвы и скорости

а) Местное обновление почвы на графике

б) Обновление почвы и скорости на IWD

5) Локальный поиск по каждому решению IWD (необязательно)

6) Глобальное обновление почвы

7) Обновление Total-Best Solution

8) Переходите к шагу 2, если не выполняется условие завершения.

Алгоритм гравитационного поиска (Rashedi, Nezamabadi-pour & Saryazdi 2009)

Алгоритм гравитационного поиска основан на закон гравитации и понятие массовых взаимодействий. Алгоритм GSA использует теорию Ньютоновская физика и его искатель агенты являются сборником масс. В GSA есть изолированная система масс. Используя силу тяжести, каждая масса в системе может увидеть ситуацию других масс. Таким образом, гравитационная сила - это способ передачи информации между различными массами (Рашеди, Незамабади-пуре и Сарьязди, 2009).^[42] В GSA агенты рассматриваются как объекты, и их производительность измеряется их массой. Все эти объекты привлекают друг друга сила тяжести сила, и эта сила вызывает движение всех объектов к объектам с более тяжелыми массами. Более тяжелые массы соответствуют лучшим решениям проблемы. В позиция агента соответствует решению задачи, а его масса определяется с помощью функции приспособленности. По прошествии времени массы притягиваются самой тяжелой массой, которая в идеале представляет собой оптимальное решение в пространстве поиска. GSA можно рассматривать как изолированную систему масс. Это похоже на небольшой искусственный мир масс, подчиняющийся ньютоновским законам гравитации и движения.^[43] Многоцелевой вариант GSA, названный MOGSA, впервые был предложен Hassanzadeh et al. в 2010.^[44]

Поиск кукушки (Ян и Деб, 2009)

Основная статья: Кукушка поиск

В исследование операций, поиск кукушки является оптимизация алгоритм разработан Синь-ши Ян и Суаш Деб в 2009 году.^[45][46] Он был вдохновлен облигатный паразитизм расплода некоторых кукушка вида, откладывая яйца в гнезда других птиц-хозяев (других видов). Некоторые птицы-хозяева могут вступать в прямой конфликт с вторгающимися кукушками. Например, если птица-хозяин обнаруживает, что яйца не принадлежат ей, она либо выбросит эти инопланетные яйца, либо просто покинет свое гнездо и построит новое гнездо в другом месте. Некоторые виды кукушек, такие как Новый мир выводок-паразит Tapera эволюционировали таким образом, что самки кукушки-паразита часто очень специализированы в мимикрии окраски и рисунка яиц нескольких выбранных видов хозяев.^[47]

Алгоритм летучей мыши (Ян 2010)

Основная статья: Алгоритм летучей мыши

Алгоритм летучих мышей - это алгоритм на основе интеллекта роя, вдохновленный эхолокация поведение микробаты. BA автоматически уравновешивает исследование (прыжки на большие расстояния по глобальному пространству поиска, чтобы избежать застревания около одного локального максимума) с использованием (более подробный поиск известных хороших решений для поиска локальных максимумов), контролируя громкость и скорость излучения импульсов смоделированных летучих мышей в многомерное пространство поиска.^[48]

Алгоритм спиральной оптимизации (SPO) (Тамура и Ясуда 2011, 2016-2017)

Основная статья: Алгоритм спиральной оптимизации

Алгоритм спиральной оптимизации (SPO)

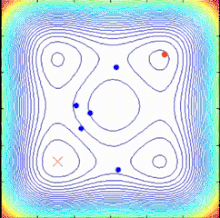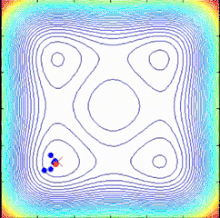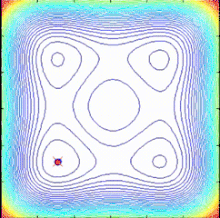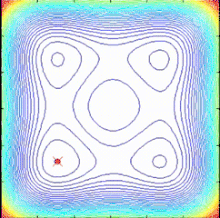
В спираль Алгоритм оптимизации (SPO) - это несложная концепция поиска, вдохновленная спиральными явлениями в природе. Мотивация сосредоточить внимание на спиральных явлениях была вызвана пониманием того, что динамика, порождающая логарифмические спирали, разделяет поведение диверсификации и интенсификации. Поведение диверсификации может работать для глобального поиска (исследования), а поведение интенсификации позволяет интенсивный поиск текущего найденного хорошего решения (эксплуатации). Алгоритм SPO - это алгоритм многоточечного поиска, не имеющий градиента целевой функции, который использует несколько спиральных моделей, которые можно описать как детерминированные динамические системы. Поскольку точки поиска следуют по логарифмическим спиральным траекториям к общему центру, определяемому как текущая лучшая точка, могут быть найдены лучшие решения и общий центр может быть обновлен.^[49]

Алгоритм опыления цветов (Ян 2012)

Алгоритм опыления цветов - это метаэвристический алгоритм это было разработано Синь-Ши Ян,^[50] на основе опыление процесс цветения растения.

Этот алгоритм имеет 4 правила или предположения:

1. Биотический и перекрестное опыление рассматривается как глобальный процесс опыления, когда опылители, несущие пыльцу, выполняют Леви рейсы.
2. Абиотический и самоопыление считаются местным опылением.
3. Цветочное постоянство можно рассматривать как вероятность воспроизводства пропорциональный к подобию двух задействованных цветов.
4. Локальное и глобальное опыление контролируется вероятностью переключения^{[требуется разъяснение ]} ${\displaystyle p\in [0,1]}$. Из-за физической близости и других факторов, таких как ветер, местное опыление может иметь значительную долю q в общей деятельности по опылению.

Эти правила можно преобразовать в следующие уравнения обновления:

${\displaystyle x_{i}^{t+1}=x_{i}^{t}+L(x_{i}^{t}-g_{*})}$

${\displaystyle x_{i}^{t+1}=x_{i}^{t}+\epsilon (x_{i}^{t}-x_{k}^{t})}$

где ${\displaystyle x_{i}^{t}}$ - вектор решения и ${\displaystyle g_{*}}$ - текущий лучший результат, найденный на данный момент во время итерации. Вероятность переключения между двумя уравнениями во время итераций равна ${\displaystyle p}$. К тому же, ${\displaystyle \epsilon }$ - случайное число, полученное из равномерного распределения. ${\displaystyle L}$ - размер шага, взятый из распределения Леви.

Полеты Леви с использованием шагов Леви - это мощное случайное блуждание, потому что возможности глобального и локального поиска могут выполняться одновременно. В отличие от стандартных случайных блужданий, у полетов Леви есть случайные прыжки в длину, которые позволяют алгоритму выпрыгивать из любых местных долин. Шаги Леви подчиняются следующему приближению:

${\displaystyle L\sim {\frac {1}{s^{1+\beta }}},}$

где ${\displaystyle \beta }$ - показатель Леви.^[51] Правильно нарисовать шаги Леви может быть непросто, и простой способ создания полетов Леви ${\displaystyle s}$ использовать два нормальных распределения ${\displaystyle u}$ и ${\displaystyle v}$ преобразованием^[52]

${\displaystyle s={\frac {u}{|v|^{1+\beta }}},}$

с

${\displaystyle u\sim N(0,\sigma ^{2}),\quad v\sim N(0,1),}$

где ${\displaystyle \sigma }$ является функцией ${\displaystyle \beta }$.

Алгоритм оптимизации Cuttlefish (Eesa, Mohsin, Brifcani & Orman, 2013)

Шесть случаев отражения, используемых каракатицей

Алгоритм оптимизации каракатиц основан на популяции алгоритм поиска вдохновленный изменением цвета кожи поведением Каракатица который был разработан в 2013 году^[53][54] В нем есть два глобальных поиска и два локальных поиска.

Алгоритм рассматривает два основных процесса: Отражение и Видимость. Процесс отражения имитирует механизм отражения света, а видимость имитирует видимость совпадающих узоров. Эти два процесса используются в качестве стратегии поиска для поиска глобального оптимального решения. Постановка поиска нового решения (новыйP) используя отражение и видимость как следует:${\displaystyle newP=Reflection+Visibility}$

CFA делит популяцию на 4 группы (G1, G2, G3 и G4). Для G1 алгоритм применяет случай 1 и 2 (взаимодействие между хроматофорами и иридофорами) для получения новых решений. Эти два случая используются как глобальный поиск. Для G2 алгоритм использует случай 3 (опаератор отражения иридофоров) и случай 4 (взаимодействие между иридофорами и хроматофорами) для получения новых решений) в качестве локального поиска. В то время как для G3 взаимодействие между лейкофорами и хроматофорами (случай 5) используется для получения решений вокруг лучшего решения (локальный поиск). Наконец, для G4 случай 6 (оператор отражения лейкофоров) используется в качестве глобального поиска путем отражения любого входящего света без каких-либо изменений. Основной этап CFA описывается следующим образом:

   1 Инициализировать численность населения (п[N]) с случайный решения, Назначить то значения из r1, r2, v1, v2.   2 Оценить то численность населения и Держать то Лучший решение.   3 Делить численность населения в четыре группы (G1, G2, G3 и G4).   4 Повторение         4.1 Рассчитать то средний ценить из то Лучший решение.        4.2 за (каждый элемент в G1)                     генерировать новый решение с помощью случай(1 и 2)        4.3 за (каждый элемент в G2)                     генерировать новый решение с помощью случай(3 и 4)        4.4 за (каждый элемент в G3)                     генерировать новый решение с помощью случай(5)        4.5 за (каждый элемент в G4)                     генерировать новый решение с помощью случай(6)        4.6 Оценить то новый решения    5. До того как (остановка критерий является встретились)   6. Вернуть то Лучший решение

Уравнения, которые используются для расчета отражения и видимости для четырех групп, описаны ниже:

Варианты 1 и 2 для G1:

${\displaystyle Reflection[j]=R*G_{1}[j].Points[j]}$

${\displaystyle Visibility[j]=V*(Best.Points[j]-G_{1}[i].Points[j])}$

Варианты 3 и 4 для G2:

${\displaystyle Reflection[j]=R*Best.Points[j]}$

${\displaystyle Visibility[j]=V*(Best.Points[j]-G_{2}[i].Points[j])}$

Случай 5 для G3:

${\displaystyle Reflection[j]=R*Best.Points[j]}$

${\displaystyle Visibility[j]=V*(Best.Points[j]-AV_{Best}}$

Случай 6 для G4:

${\displaystyle P[i].Points[j]=random*(upperLimit-lowerLinit)+LowerLimit,i=1,2,...,N;j=1,2,...,d}$

Где ${\displaystyle G_{1}}$, ${\displaystyle G_{2}}$ это Group1 и Group2, я представляет ${\displaystyle i^{th}}$ элемент в грамм, j это ${\displaystyle j^{th}}$ точка ${\displaystyle i^{th}}$ элемент в группе грамм, Лучший это лучшее решение и ${\displaystyle AV_{Best}}$ представляет собой среднее значение Лучший точки. В то время как р и V два случайных числа, произведенных около нуля, например между (-1, 1), р представляет степень отражения, V представляет степень видимости окончательного вида рисунка, верхний предел и Нижний предел - верхний предел и нижний предел проблемной области.

Алгоритм гетерогенных распределенных пчел (Ткач и др., 2013)

Алгоритм гетерогенных распределенных пчел (HDBA), также известный как модифицированный распределенный алгоритм пчел (MDBA), является мультиагентным метаэвристический алгоритм, впервые представленный Ткачем и его сотрудниками в 2013 году,^[55][56] разработан в рамках его кандидатской диссертации. HDBA использует вероятностную технику, вдохновленную поведением пчел при кормлении. Это позволяет решить комбинаторная оптимизация проблемы с несколькими разнородными агентами, которые обладают разными возможностями и производительностью. Окончательный механизм принятия решений использует правило выбора колеса, в котором каждый агент имеет вероятность, с которой он выбирает решение. Впервые он был применен в случае неоднородных датчиков в задаче распознавания цели для повышения производительности системы путем сопоставления функции полезности датчиков со значением их характеристик. Впоследствии это было успешно применено к другим проблемам, включая проблему распределения полицейских агентов по преступлениям и выработку почти оптимальных решений проблемы коммивояжера.

Алгоритм искусственной экосистемы (Бачиньский, 2013)

Алгоритм искусственной экосистемы (AEA) - это вероятностный метод оптимизации, основанный на некоторых явлениях, происходящих в природных экосистемах. Отношения между индивидами моделируются как их взаимоотношениями внутри одной группы, так и отношениями между индивидами, принадлежащими к разным группам, сосуществующими как часть экологической системы. Есть три основных типа организмов: растения, травоядные и хищники. Все типы организмов воспроизводятся (скрещиваются и видоизменяются) внутри своих собственных видов. Как метод, он включает в себя некоторые эволюционные алгоритмы и элементы PSO с дополнительными расширениями. Это довольно сложный метод, но он показал себя способным решать как задачи непрерывной, так и комбинаторной оптимизации.^[57]

Оптимизация кооперативной группы (2014)

Система кооперативной групповой оптимизации (CGO)^[58][59] - это метаэвристическая структура для реализации экземпляров алгоритмов путем интеграции преимуществ совместной группы и низкоуровневого проектирования портфеля алгоритмов. Следуя вдохновленной природой парадигме кооперативной группы, агенты не только исследуют параллельно своей индивидуальной памяти, но также сотрудничают со своими сверстниками через групповую память. Каждый агент имеет портфель (гетерогенных) встроенных эвристик поиска (ESH), в котором каждый ESH может перевести группу в автономный CGO-кейс, а гибридные CGO-кейсы в алгоритмическом пространстве могут быть определены с помощью кооперативного поиска на низком уровне среди портфель алгоритмов (ESH) посредством настраиваемого совместного использования памяти. Пассивный лидер группы может также облегчить процесс оптимизации за счет кодирования знаний в среде поиска. Он применялся как для численной, так и для комбинаторной оптимизации.

Искусственный интеллект роя (Розенберг 2014)

Под искусственным роевым интеллектом в реальном времени понимается замкнутая система людей-пользователей, подключенных через Интернет и структурированная в рамках, смоделированных по образцу естественных роей, таким образом, что она вызывает коллективную мудрость группы как единый возникающий разум.^[60][61] Таким образом, человеческие рои могут отвечать на вопросы, делать прогнозы, принимать решения и решать проблемы, коллективно исследуя разнообразные варианты и синхронно находя предпочтительные решения. Изобретенный Доктор Луи Розенберг В 2014 году методология ASI стала известна своей способностью делать точные коллективные прогнозы, превосходящие результаты отдельных членов роя.^[62] В 2016 году искусственный интеллект роя от Единогласный А. репортер попросил предсказать победителей Кентукки Дерби, и успешно выбрал первых четырех лошадей по порядку, превзойдя коэффициент 540: 1.^[63][64]

Оптимизация сталкивающихся тел (Кавех и Махдави, 2014)

Оптимизация сталкивающихся тел (CBO)^[65] Алгоритм был создан Каве и Махдави в 2014 году на основе законов количества движения и энергии. Этот алгоритм не зависит от каких-либо внутренних параметров, а также чрезвычайно прост в реализации, использовании и использовании в различных типах инженерных задач.^[66]

Алгоритм дуэлянта (Biyanto 2016)

Алгоритм дуэлянта относится к алгоритму оптимизации на основе генов, аналогичному Генетические алгоритмы. Алгоритм дуэлянтов начинается с первоначального набора дуэлянтов. Поединок заключается в определении победителя и проигравшего. Проигравший учится у победителя, а победитель пробует свои новые навыки или приемы, которые могут улучшить их боевые способности. Несколько дуэлянтов с высокими боевыми способностями называются чемпионом. Чемпион тренирует нового дуэлянта, исходя из своих возможностей. Новый дуэлянт присоединится к турниру как представитель каждого чемпиона. Все дуэлянты переоцениваются, и дуэлянты с худшими боевыми способностями удаляются, чтобы сохранить количество дуэлянтов.^[67]

Оптимизация Харриса Ястреба (Хейдари и др., 2019)

Оптимизатор Harris hawks (HHO) вдохновляет охота стратегии Ястреб Харриса и избегая шаблонов кролики в природа.^[68]

Алгоритм касаток (Биянто, 2016)

Killer Whale Algorithm - это алгоритм, вдохновленный жизнью косаток. Философия алгоритма - это модели движения косаток при охоте на добычу и социальная структура косаток. Новизна этого алгоритма включает "запоминать способность"Косатки" в алгоритме.^[69]

Алгоритм дождевой воды (Biyanto 2017)

"Физические движения капель дождя с использованием движения закона Ньютона"был вдохновлен авторами на создание этого алгоритма. Каждая капля дождя представляет собой случайные значения оптимизированных переменных, которые различаются по массе и высоте. Она упадет на землю, следуя"движение свободного падения"со скоростью квадратный корень из времени ускорения свободного падения. Следующее движение"равномерно ускоренное движение"по пути капли дождя, чтобы достичь самого низкого места на земле. Самое низкое место в земле является целевой функцией этого алгоритма.^[70]

Алгоритм баланса массы и энергии (Biyanto 2018)

Баланс массы и энергии является фундаментальным "законы физики"утверждает, что масса не может быть ни произведена, ни уничтожена. Она только сохраняется. Не менее фундаментальным является закон сохранения энергии. Хотя энергия может меняться по форме, она также не может быть создана или уничтожена. Красота этого алгоритма заключается в возможности для достижения глобального оптимального решения, одновременно работая либо "минимизировать и максимизировать метод поиска".

Алгоритм гидрологического цикла (Wedyan et al., 2017)

Предлагается новый природный алгоритм оптимизации, называемый алгоритмом гидрологического цикла (HCA), основанный на непрерывном движении воды в природе. В HCA коллекция капель воды проходит через различные стадии гидрологического цикла воды, такие как поток, испарение, конденсация и осадки. Каждый этап играет важную роль в выработке решений и предотвращении преждевременной конвергенции. HCA передает информацию путем прямой и косвенной связи между каплями воды, что улучшает качество раствора. HCA предоставляет альтернативный подход к решению различных типов задач оптимизации, а также общую структуру для алгоритмов частиц на водной основе в целом.^[71]

Колония императорских пингвинов (Харифи и др., 2019)

Этот алгоритм представляет собой новый метаэвристический алгоритм, вдохновленный поведением императорских пингвинов, обитающих в Антарктиде. EPC контролируется тепловым излучением тела пингвинов и их спиралевидным движением в своей колонии. Императорские пингвины в колонии стремятся создать соответствующее тепло и регулировать температуру своего тела, и это тепло полностью координируется и контролируется движениями пингвинов.^[72]

Алгоритм Momentum Balance (MBA) (Биянто и др., 2019)

Основная статья: Алгоритм моментального баланса

Баланс импульса - это один из трех фундаментальных «законов физики», согласно которому масса, энергия и импульс только сохраняются. Использование баланса импульса было предложено во многих приложениях.^[73][74][75]

В этом исследовании был принят баланс импульса для получения идеально упругого столкновения. В идеальном, идеально упругом столкновении нет потерь кинетической энергии на другие формы, такие как потенциальная энергия, тепло и шум. Красота этого алгоритма так же проста, как и детерминированные алгоритмы оптимизации, однако алгоритм баланса импульса имеет возможность достичь глобального оптимального решения.

Алгоритм оптимизации Shuffled Shepherd (SSOA) (Kaveh and Zaerreza 2020)

Основная статья: Алгоритм оптимизации Shuffled Shepherd

Этот метод представляет собой новый алгоритм метаэвристической оптимизации с участием нескольких сообществ. В этом алгоритме агенты сначала разделяются на несколько сообществ, а затем выполняется процесс оптимизации, имитирующий поведение пастуха в природе, действующего в каждом сообществе.^[76]

Алгоритм оптимизации поденок (MA) (Zervoudakis & Tsafarakis 2020)

Основная статья: Алгоритм оптимизации поденок

Алгоритм оптимизации поденок был разработан для решения как непрерывных, так и дискретных задач оптимизации и основан на поведении поденок и процессе спаривания поденок. Процессы брачного танца и случайного полета улучшают баланс между исследовательскими и эксплуатационными свойствами алгоритма и помогают ему выйти из локальных оптимумов. По производительности алгоритм поденок превосходит другие популярные метаэвристики, такие как PSO, DE, GA и FA, с точки зрения скорости сходимости и скорости сходимости. ^[77]

Политический оптимизатор (ПО) (Камар Аскари, Ирфан Юнас и Мехрин Саид, 2020 г.)

Основная статья: Политический оптимизатор

Политический оптимизатор (PO) - это алгоритм, основанный на социальном поведении человека, вдохновленный многопартийной политической системой. Источник вдохновения сформулирован как набор из 5 этапов: формирование партии и распределение избирательных округов, смена партий, избирательная кампания, межпартийные выборы и парламентские дела. У PO есть две уникальные особенности: логическое разделение совокупности для присвоения двойной роли каждому возможному решению и стратегия обновления позиции на основе недавнего прошлого (RPPUS). PO демонстрирует отличную производительность по сравнению с 15 хорошо известными метаэвристиками для 50 унимодальных и мультимодальных функций тестирования и 4 инженерных задач. ^[78]

Оптимизатор на основе кучи (HBO) (Камар Аскари, Мехрин Саид, Ирфан Юнас, 2020 г.)

Основная статья: Оптимизатор на основе кучи

HBO - это метаэвристика, основанная на социальном поведении человека, вдохновленная корпоративной иерархией рангов и взаимодействием между сотрудниками, организованными в иерархию. Уникальность HBO заключается в использовании структуры данных кучи для моделирования иерархического расположения сотрудников и введении параметра (γ) для альтернативного включения исследования и эксплуатации. Более того, три уравнения, выведенные для трех фаз HBO, вероятностно объединены, чтобы уравновесить разведку и разработку. HBO демонстрирует потрясающую производительность в 97 тестах и ​​3 задачах машиностроения. ^[79]

Алгоритм криминалистического расследования (ФБР) (Дж. С. Чоу и Н. М. Нгуен, 2020 г.)

Основная статья: Оптимизатор ФБР

Основной мотивацией для разработки нового алгоритма является его способность эффективно решать различные задачи оптимизации. Новый метод оптимизации, алгоритм криминалистического расследования (FBI), разработан для определения глобальных решений для непрерывных нелинейных функций с низкими вычислительными затратами и высокой точностью. ФБР вдохновлено процессом полицейских «расследование - местонахождение - преследование». Основные особенности FBI: (1) FBI - алгоритм оптимизации без параметров; (2) ФБР значительно превзошло хорошо известные и недавно разработанные алгоритмы; (3) ФБР имеет короткое время вычислений и быстро находит оптимальные решения при решении проблем; (4) ФБР эффективно в решении задач большой размерности (D = 1000); и (5) в структуре ФБР есть две команды, которые хорошо сочетают разведку и разработку.

Подробности можно найти по адресу: Chou J-S, Nguyen N-M, Метаоптимизация, вдохновленная ФБР, Applied Soft Computing, 2020: 106339, ISSN 1568-4946, https://doi.org/10.1016/j.asoc.2020.106339 ^[80]

Поиск медуз (JS) (JS Chou and DN Truong, 2021)

Основная статья: Оптимизатор поиска медузы

Визуализация JS для поиска глобального минимума математической функции.

Оптимизатор Jellyfish Search (JS) вдохновлен поведением медуз в океане. Моделирование поискового поведения медуз включает в себя их следование за океанским течением, их движения внутри роя медуз (активные движения и пассивные движения), механизм контроля времени для переключения между этими движениями и их схождение в цветение медуз. Новый алгоритм успешно протестирован на тестовых функциях и задачах оптимизации. Примечательно, что JS имеет только два управляющих параметра, а именно размер популяции и количество итераций. Следовательно, JS очень прост в использовании и потенциально является отличным метаэвристическим алгоритмом для решения задач оптимизации. ^[81]

Критика методологии метафоры

В то время как метаэвристика, вдохновленная отдельными метафорами, дает удивительно эффективные решения конкретных проблем,^[82] Метаэвристика, вдохновленная метафорами, в целом вызывает критику в исследовательском сообществе за то, что скрывает свою неэффективность или новизну за сложной метафорой.^[82][83] Кеннет Соренсен отметил, что:^[84]

В последние годы в области комбинаторная оптимизация стал свидетелем настоящего цунами «новых» метаэвристических методов, большинство из которых основано на метафоре какого-то естественного или искусственного процесса. Поведение практически любых видов насекомых, поток воды, совместная игра музыкантов - кажется, ни одна идея не является слишком надуманной, чтобы служить вдохновением для запуска еще одной метаэвристики. [Я] буду утверждать, что это направление исследований угрожает увести область метаэвристики от научной строгости.

Соренсен и Гловер заявил, что:^[85]

Большое (и растущее) количество публикаций посвящено разработке (предположительно) новых метаэвристических структур, основанных на метафорах. Список естественных или антропогенных процессов, который был использован в качестве основы для метаэвристической схемы, теперь включает такие разнообразные процессы, как добыча пищи бактериями, формирование реки, биогеография, музыканты, играющие вместе, электромагнетизм, сила тяжести, колонизация империей, взрывы мин, чемпионаты лиг, облака и так далее. Важная подкатегория находится в метаэвристике, основанной на поведении животных. Муравьи, пчелы, летучие мыши, волки, кошки, светлячки, орлы, дельфины, лягушки, лосось, стервятники, термиты, мухи и многие другие - все они были использованы для создания «новой» метаэвристики. [...] Как правило, публикация статей по метаэвристике, основанной на метафорах, ограничивается журналами и конференциями второго уровня, но из этого правила можно найти некоторые недавние исключения. Соренсен (2013) заявляет, что исследования в этом направлении в корне ошибочны. Наиболее важно то, что автор утверждает, что новизна основной метафоры не делает автоматически получившуюся основу «новой». Напротив, появляется все больше свидетельств того, что очень немногие из метафорических методов являются новыми в каком-либо интересном смысле.

В ответ, Springer с Журнал эвристики обновили свою редакционную политику, заявив, что:^[86]

Предложение новых парадигм допустимо только в том случае, если они содержат новаторские базовые идеи, такие как те, которые встроены в классические концепции, такие как генетические алгоритмы, табу поиск, и имитация отжига. Журнал эвристики избегает публикации статей, которые переупаковывают и внедряют старые идеи в методы, которые, как утверждается, основаны на метафорах естественных или созданных руками человека систем и процессов. Эти так называемые «новые» методы используют аналогии, которые варьируются от умные капли воды, музыканты, играющие джаз, империалистические общества, чехарда, кенгуру, все виды стай и насекомых и даже процессы взрыва мин (Sörensen, 2013). Если исследователь использует метафору, чтобы стимулировать свои собственные идеи о новом методе, метод, тем не менее, должен быть переведен на язык, свободный от метафор, чтобы применяемые стратегии можно было четко понять, а их новизна была ясно видна. (См. Пункты 2 и 3 ниже.) Метафоры дешевы, и их легко найти. Их использование для «демонстрации» метода неприемлемо ».

[...] Реализации следует объяснять, используя стандартную терминологию оптимизации, где решение называется «решением», а не что-то еще, связанное с какой-то неясной метафорой (например, гармония, мухи, летучие мыши, страны, так далее.).

[...] Журнал эвристики полностью поддерживает точку зрения Соренсена о том, что метафорические «новые» методы не должны публиковаться, если они не могут продемонстрировать вклад в свою область. Переименование существующих концепций не считается вкладом. Несмотря на то, что эти методы часто называют «новыми», многие из них не предлагают новых идей, за исключением случайных маргинальных вариантов уже существующей методологии. Эти методы не должны занимать пространство журнала для действительно новаторских идей и исследований. Поскольку они не используют стандартный словарь оптимизации, их излишне трудно понять.

Политика Springer журнал 4OR - Ежеквартальный журнал исследований операций состояния^[87]

Акцент на научную строгость и инновации подразумевает, в частности, что журнал не публикует статьи, которые просто предлагают замаскированные варианты известных методов без надлежащей проверки (например, метаэвристика, которая считается «эффективной» только на основе метафорических сравнений. с естественными или искусственными системами и процессами). Новые методы должны быть представлены языком без метафор, устанавливая их связь с классическими парадигмами. Их свойства должны быть установлены на основе убедительных с научной точки зрения аргументов: математических доказательств, контролируемых экспериментов, объективных сравнений и т. Д.

Смотрите также

• Интеллект роя # Алгоритмы

Примечания

1. Колорни, Альберто; Дориго, Марко; Маниеццо, Витторио (1992). «Распределенная оптимизация колониями муравьев». В Вареле, Франсиско Дж .; Бургин, Поль (ред.). К практике автономных систем: материалы первой европейской конференции по искусственной жизни. С. 134–42. ISBN  978-0-262-72019-9.
2. М. Дориго, Оптимизация, обучение и естественные алгоритмыДокторская диссертация, Миланский политехнический университет, Италия, 1992.^{[страница нужна ]}
3. Злочин, Марк; Бираттари, Мауро; Мёло, Николя; Дориго, Марко (2004). "Модельно-ориентированный поиск комбинаторной оптимизации: критический обзор". Анналы исследований операций. 131 (1–4): 373–95. CiteSeerX  10.1.1.3.427. Дои:10.1023 / B: ANOR.0000039526.52305.af.
4. Kennedy, J .; Эберхарт, Р. (1995). «Оптимизация роя частиц». Материалы ICNN'95 - Международной конференции по нейронным сетям. 4. С. 1942–8. CiteSeerX  10.1.1.709.6654. Дои:10.1109 / ICNN.1995.488968. ISBN  978-0-7803-2768-9.
5. Shi, Y .; Эберхарт Р. (1998). «Модифицированный оптимизатор роя частиц». 1998 Международная конференция IEEE по эволюционным вычислениям. Всемирный конгресс IEEE по вычислительному интеллекту (каталожный номер 98TH8360). С. 69–73. Дои:10.1109 / ICEC.1998.699146. ISBN  978-0-7803-4869-1.
6. Кеннеди, Дж. (1997). «Рой частиц: социальная адаптация знаний». Материалы Международной конференции IEEE 1997 г. по эволюционным вычислениям (ICEC '97). С. 303–8. Дои:10.1109 / ICEC.1997.592326. ISBN  978-0-7803-3949-1.
7. Kennedy, J .; Эберхарт, Р. (2001). Рой Интеллект. Морган Кауфманн. ISBN  978-1-55860-595-4.
8. Поли, Р. (2007). «Анализ публикаций по приложениям оптимизации роя частиц» (PDF). Технический отчет CSM-469. Департамент компьютерных наук, Университет Эссекса, Великобритания. Архивировано из оригинал (PDF) на 2011-07-16. Получено 2016-08-31.
9. Поли, Риккардо (2008). «Анализ публикаций по применению оптимизации роя частиц». Журнал искусственной эволюции и приложений. 2008: 1–10. Дои:10.1155/2008/685175.
10. Боньяди, Мохаммад Реза; Михалевич, Збигнев (2017). "Оптимизация роя частиц для задач с одной целью в непрерывном пространстве: обзор". Эволюционные вычисления. 25 (1): 1–54. Дои:10.1162 / EVCO_r_00180. PMID  26953883.
11. Zong Woo Geem; Джун Хун Ким; Логанатан, Г.В. (2016). «Новый алгоритм эвристической оптимизации: поиск гармонии». Моделирование. 76 (2): 60–8. Дои:10.1177/003754970107600201.
12. Вейланд, Деннис (2015). «Критический анализ алгоритма поиска гармонии - как не разгадывать судоку». Перспективы исследования операций. 2: 97–105. Дои:10.1016 / j.orp.2015.04.001.
13. Сака, М. (2016). «Метаэвристика в структурной оптимизации и обсуждение алгоритма поиска гармонии». Рой и эволюционные вычисления. 28: 88–97. Дои:10.1016 / j.swevo.2016.01.005.
14. "Код HS для судоку".
15. Джем, Зонг Ву (2006). «Оптимальное стоимостное проектирование водопроводных сетей с использованием поиска гармонии». Инженерная оптимизация. 38 (3): 259–277. Дои:10.1080/03052150500467430.
16. Gholizadeh, S .; Барзегар, А. (2013). «Оптимизация формы конструкций для частотных ограничений с помощью алгоритма последовательного поиска гармонии». Инженерная оптимизация. 45 (6): 627. Bibcode:2013EnOp ... 45..627G. Дои:10.1080 / 0305215X.2012.704028.
17. Geem, Zong Woo; Ли, Кан Сок; Пак, Ёнджин (2005). «Применение поиска гармонии к маршрутизации транспортных средств». Американский журнал прикладных наук. 2 (12): 1552. Дои:10.3844 / ajassp.2005.1552.1557.
18. Ван, Линг; Ли, Линг-по (2013). «Эффективный алгоритм поиска дифференциальной гармонии для решения невыпуклых задач распределения экономической нагрузки». Международный журнал электроэнергетических и энергетических систем. 44: 832–843. Дои:10.1016 / j.ijepes.2012.08.021.
19. Некоэй, Комаил; Farsangi, Malihe M .; Незамабади-Пур, Хоссейн; Ли, Кван Ю. (2013). «Улучшенный многоцелевой поиск гармонии для оптимального размещения DG в системах распределения». Транзакции IEEE в интеллектуальной сети. 4: 557–567. Дои:10.1109 / TSG.2012.2237420.
20. Хадван, Мохаммед; Айоб, Масри; Sabar, Nasser R .; Ку, Roug (2013). «Алгоритм поиска гармонии для задач составления списка медсестер». Информационные науки. 233: 126–140. CiteSeerX  10.1.1.298.6805. Дои:10.1016 / j.ins.2012.12.025.
21. Хоанг, Дык Чинь; Ядав, Парикшит; Кумар, Раджеш; Панда, Санджиб Кумар (2014). "Реализация в реальном времени протокола кластеризации на основе алгоритма поиска гармонии для энергоэффективных беспроводных сенсорных сетей". IEEE Transactions по промышленной информатике. 10: 774–783. Дои:10.1109 / TII.2013.2273739.
22. Рен Диао; Цян Шэнь (2012). «Выбор характеристик с поиском гармонии». Транзакции IEEE по системам, человеку и кибернетике - Часть B: Кибернетика. 42 (6): 1509–23. Дои:10.1109 / TSMCB.2012.2193613. PMID  22645272.
23. Фаттахи, Хади; Голами, Амин; Амирибахтияр, Мохаммад Садех; Моради, Сиямак (2014). «Оценка осаждения асфальтенов по данным титрования: гибридная опорная векторная регрессия с поиском гармонии». Нейронные вычисления и приложения. 26 (4): 789. Дои:10.1007 / s00521-014-1766-y.
24. «Алгоритм поиска гармонии».
25. Manjarres, D .; Ланда-Торрес, I .; Gil-Lopez, S .; Del Ser, J .; Bilbao, M.N .; Salcedo-Sanz, S .; Geem, Z.W. (2013). «Обзор применений алгоритма поиска гармонии». Инженерные приложения искусственного интеллекта. 26 (8): 1818. Дои:10.1016 / j.engappai.2013.05.008.
26. Ассиф Асад; Глубоко, Кусум (2016). "Применение алгоритма поиска гармонии в интеллектуальном анализе данных: обзор". Труды Пятой Международной конференции по мягким вычислениям для решения проблем. Достижения в интеллектуальных системах и вычислениях. 437. С. 863–74. Дои:10.1007/978-981-10-0451-3_77. ISBN  978-981-10-0450-6.
27. Карабога, Дервис (2010). «Алгоритм искусственной пчелиной семьи». Scholarpedia. 5 (3): 6915. Bibcode:2010SchpJ ... 5,69 15 тыс.. Дои:10.4249 / scholarpedia.6915.
28. Фам Д.Т., Ганбарзаде А., Коч Э., Отри С., Рахим С. и Заиди М. Алгоритм пчел. Техническая записка, Технологический центр, Кардиффский университет, Великобритания, 2005^{[страница нужна ]}
29. Pham, D T; Кастеллани, М. (2009). «Алгоритм пчел: моделирование пищевого поведения для решения задач непрерывной оптимизации». Труды Института инженеров-механиков, часть C: журнал машиностроения. 223 (12): 2919. Дои:10.1243 / 09544062jmes1494.
30. Krishnanand, K.N .; Гхош, Д. (2005). «Обнаружение нескольких мест расположения источников с использованием метафоры светлячка с приложениями к коллективной робототехнике». Труды 2005 IEEE Swarm Intelligence Symposium, 2005. SIS 2005. С. 84–91. Дои:10.1109 / SIS.2005.1501606. ISBN  978-0-7803-8916-8.
31. Юсуфф, Музаффар; Лэнси, Кевин; Паша, Файзул (2006). «Перемешанный алгоритм прыжка лягушки: меметическая метаэвристика для дискретной оптимизации». Инженерная оптимизация. 38 (2): 129. Дои:10.1080/03052150500384759.
32. Чу, Шу-Чуань; Цай, Пэй-вэй; Пан, Дженг-Шян (2006). «Оптимизация роя кошек». PRICAI 2006: Тенденции в области искусственного интеллекта. Конспект лекций по информатике. 4099. Гуйлинь, Китай. С. 854–858. Дои:10.1007/11801603_94. ISBN  978-3-540-36667-6.
33. Аташпаз-Гаргари, Эсмаил; Лукас, Каро (2007). «Империалистический конкурентный алгоритм: алгоритм оптимизации, вдохновленный империалистической конкуренцией». 2007 IEEE Конгресс по эволюционным вычислениям. С. 4661–7. Дои:10.1109 / CEC.2007.4425083. ISBN  978-1-4244-1339-3.
34. Хоссейни, Сейедмохсен; Аль-Халед, Абдулла (2014). «Обзор метаэвристического алгоритма империалистической конкуренции: внедрение в инженерной области и направления будущих исследований». Прикладные мягкие вычисления. 24: 1078–1094. Дои:10.1016 / j.asoc.2014.08.024.
35. Nazari-Shirkouhi, S .; Eivazy, H .; Ghodsi, R .; Rezaie, K .; Аташпаз-Гаргари, Э. (2010). «Решение комплексной проблемы аутсорсинга ассортимента продукции с использованием алгоритма империалистической конкуренции». Экспертные системы с приложениями. 37 (12): 7615. Дои:10.1016 / j.eswa.2010.04.081.
36. Акл, Селим Г .; Calude, Cristian S .; Диннин, Майкл Дж .; Розенберг, Гжегож; Тодд Уэрхэм, Х. (2007). Нетрадиционные вычисления. Конспект лекций по информатике. 4618. arXiv:0711.2964. Дои:10.1007/978-3-540-73554-0. ISBN  978-3-540-73553-3.
37. Рабанал, Пабло; Родригес, Исмаэль; Рубио, Фернандо (2009). «Применение динамики речного образования для решения NP-полных задач». Вдохновленные природой алгоритмы оптимизации. Исследования в области вычислительного интеллекта. 193. С. 333–68. Дои:10.1007/978-3-642-00267-0_12. ISBN  978-3-642-00266-3.
38. Амин, Саман Хамид; Al-Raweshidy, H.S .; Аббас, Рафед Саббар (2014). «Интеллектуальный протокол маршрутизации пакетов данных». Компьютерная сеть. 62: 162–181. Дои:10.1016 / j.bjp.2013.11.015.
39. Редларски, Гжегож; Палковский, Александр; Домбковский, Мариуш (2013). «Использование алгоритма динамики речных образований в навигации мобильных роботов». Явления твердого тела. 198: 138–143. Дои:10.4028 / www.scientific.net / SSP.198.138.
40. Рабанал, Пабло; Родригес, Исмаэль; Рубио, Фернандо (2017). «Приложения динамики речного образования». Журнал вычислительной науки. 22: 26–35. Дои:10.1016 / j.jocs.2017.08.002.
41. Хоссейни, Хамед Шах (2009). «Интеллектуальный алгоритм капель воды: вдохновленный природой алгоритм оптимизации на основе роя». Международный журнал биологических вычислений. 1: 71. Дои:10.1504 / ijbic.2009.022775.
42. Рашеди, Эсмат; Незамабади-Пур, Хоссейн; Сарязди, Саид (2009). "GSA: алгоритм гравитационного поиска". Информационные науки. 179 (13): 2232. Дои:10.1016 / j.ins.2009.03.004.
43. Рашеди, Незамабади-поре и Сарязди 2009 г.
44. Хасанзаде, Хамид Реза; Рухани, Моджтаба (2010). «Многоцелевой алгоритм гравитационного поиска». 2010 2-я Международная конференция по вычислительному интеллекту, коммуникационным системам и сетям. С. 7–12. Дои:10.1109 / CICSyN.2010.32. ISBN  978-1-4244-7837-8.
45. Ян, Синь-Шэ; Суаш Деб (2009). «Поиск с кукушкой через рейсы Леви». 2009 Всемирный конгресс по природе и биологическим вычислениям (NaBIC). С. 210–4. Дои:10.1109 / NABIC.2009.5393690. ISBN  978-1-4244-5053-4.
46. Inderscience (27 мая 2010 г.). "Кукушка рисует весну". Alphagalileo.org. Получено 2010-05-27.
47. Р. Б. Пейн, М. Д. Соренсон и К. Клиц, Кукушки, издательство Oxford University Press, (2005).^{[страница нужна ]}
48. Ян, Синь-Шэ (2010). «Новый метаэвристический алгоритм, вдохновленный летучей мышью». Стратегии сотрудничества для оптимизации, вдохновленные природой (NICSO 2010). Исследования в области вычислительного интеллекта. 284. С. 65–74. CiteSeerX  10.1.1.761.2708. Дои:10.1007/978-3-642-12538-6_6. ISBN  978-3-642-12537-9.
49. Тамура, Кеничи; Ясуда, Кейитиро (2016). «Алгоритм спиральной оптимизации с использованием периодических направлений спуска». Журнал SICE по контролю, измерениям и системной интеграции. 9 (3): 134–43. Bibcode:2016JCMSI ... 9..134T. Дои:10.9746 / jcmsi.9.134.
50. Ян, Синь-Шэ (2012). «Алгоритм опыления цветов для глобальной оптимизации». Нетрадиционные вычисления и естественные вычисления. Конспект лекций по информатике. 7445. С. 240–9. CiteSeerX  10.1.1.747.9556. Дои:10.1007/978-3-642-32894-7_27. ISBN  978-3-642-32893-0.
51. Павлюкевич, Илья (2007). «Полеты Леви, нелокальный поиск и имитация отжига». Журнал вычислительной физики. 226 (2): 1830–1844. arXiv:cond-mat / 0701653. Bibcode:2007JCoPh.226.1830P. Дои:10.1016 / j.jcp.2007.06.008.
52. X. С. Ян, Природные алгоритмы оптимизации, Elsevier, (2014).^{[страница нужна ]}
53. Иса, Адель Сабри; Брифкани, Аднан Мохсин Абдулазиз; Орман, Зейнеп (сентябрь 2013 г.). «Алгоритм каракатицы - новый алгоритм оптимизации, вдохновленный биологией». Международный журнал научных и инженерных исследований. 4 (9): 1978–86.
54. Иса, Адель Сабри; Орман, Зейнеп; Брифкани, Аднан Мохсин Абдулазиз (2015). «Новый подход к выбору характеристик, основанный на алгоритме оптимизации каракатицы для систем обнаружения вторжений». Экспертные системы с приложениями. 42 (5): 2670. Дои:10.1016 / j.eswa.2014.11.009.
55. Ткач, И .; Edan, Y .; Jevtic, A .; Ноф С.Ю. (октябрь 2013 г.). «Автоматическое распределение задач с использованием нескольких датчиков с использованием модифицированного алгоритма распределенных пчел». Международная конференция IEEE по системам, человеку и кибернетике, 2013 г.: 1401–1406. Дои:10.1109 / SMC.2013.242. ISBN  978-1-4799-0652-9.
56. Эдан, Яэль; Ноф, Шимон Й .; Евтич, Александар; Ткач, Ицхак (март 2018). «Модифицированный распределенный алгоритм пчел для распределения задач с несколькими датчиками». Датчики. 18 (3): 759. Дои:10,3390 / с18030759. ЧВК  5876720. PMID  29498683.
57. Бачиньский Дариуш, «Новая концепция алгоритма искусственной экосистемы для решения задач оптимизации», КОНТРОЛЬ И КИБЕРНЕТИКА, 45, ISSN 0324-8569, стр. 5-36, № 1
58. Се, Сяо-Фэн; Liu, J .; Ван, Цзунь-Цзин (2018). «Система совместной групповой оптимизации». Мягкие вычисления. 18 (3): 469–495. arXiv:1808.01342. Bibcode:2018arXiv180801342X. Дои:10.1007 / s00500-013-1069-8.
59. Се, Сяо-Фэн; Ван, Цзунь-Цзин (2018). «Совместная групповая оптимизация с муравьями (CGO-AS): оптимизация с использованием смешанного индивидуального и социального обучения». Прикладные мягкие вычисления. 50: 223–234. arXiv:1808.00524. Дои:10.1016 / j.asoc.2016.11.018.
60. Розенберг, Луи (12 февраля 2016 г.). «Искусственный интеллект роя, подход человека в цикле к искусственному интеллекту». Материалы 13-й ежегодной конференции AAAI по искусственному интеллекту (AAAI-16).
61. Риз, Хоуп (22 января 2016 г.). «Как« искусственный интеллект роя »использует людей, чтобы делать более точные прогнозы, чем эксперты».
62. Розенберг, Луи Б. (2015). «Рой людей - метод параллельного распределенного интеллекта в реальном времени». 2015 Семинар по смешанному разведению людей и роу (SHBI). С. 1–7. Дои:10.1109 / SHBI.2015.7321685. ISBN  978-1-4673-6522-2.
63. Катбертсон, Энтони (10 мая 2016 г.). «ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ ПРЕВРАЩАЕТ 20 ДОЛЛАРОВ В 11 000 ДОЛЛАРОВ В СТАВКЕ КЕНТУКИ ДЕРБИ (Newsweek)».
64. Олхайзер, Эбби (2 июня 2016 г.). «Что произошло, когда коллектив ИИ ответил на животрепещущие вопросы политики Reddit (Washington Post)».
65. Кавех, Али; Махдави, Вахид Реза (2014). «Оптимизация сталкивающихся тел: новый метаэвристический метод». Компьютеры и конструкции. 139: 18–27. Дои:10.1016 / j.compstruc.2014.04.005.
66. Кавех, Али; Вазириния, Ясин (2018). «Оптимизация местоположения башенного крана и количества материала между точками спроса и предложения: сравнительное исследование». Периодика Политехника Гражданское строительство. 62 (3): 732–745. Дои:10.3311 / PPci.11816.
67. Биянто, Тоток Руки; Фибрианто, Хено Йерниас; Нугрохо, Гунаван; Хатта, Агус Мухамад; Листиджорини, Эрни; Будиати, Титик; Худа, Хайрул (2016). «Алгоритм дуэлянта: алгоритм, вдохновленный тем, как дуэлянты улучшают свои возможности в дуэли». Достижения в разведке роя. Конспект лекций по информатике. 9712. С. 39–47. arXiv:1512.00708. Дои:10.1007/978-3-319-41000-5_4. ISBN  978-3-319-40999-3.
68. Хейдари, Али Асгар; Мирджалили, Сейедали; Фарис, Хоссам; Альджара, Ибрагим; Мафарджа, Маджди; Чен, Хуйлин (2019). «Оптимизация ястребов Харриса: алгоритм и приложения». Компьютерные системы будущего поколения. 97: 849–872. Дои:10.1016 / j.future.2019.02.028. ISSN  0167-739X.
69. Биянто, Тоток Р.; Матраджи; Ираван, Сонни; Febrianto, Henokh Y; Афданный, Наиндар; Рахман, Ахмад Х; Гунаван, Кевин С. Пратама, Джануар А.Д.; Бетиана, Титания N (2017). "Алгоритм касаток: алгоритм, вдохновленный жизнью косаток". Процедуры информатики. 124: 151–7. Дои:10.1016 / j.procs.2017.12.141.
70. Биянто, Т. Р.; Матраджи; Syamsi, M N; Фибрианто, H Y; Афданный, Н; Рахман, А Н; Gunawan, K S; Пратама, J A D; Мальвиндасари, А; Абдилла, A I; Bethiana, TN; Путра, Ю.А. (2017). «Оптимизация энергоэффективности и энергосбережения в проектировании экологически чистых зданий с использованием алгоритмов Duelist, Killer-Whale и Rain-Water». Серия конференций IOP: Материаловедение и инженерия. 267 (1): 012036. Bibcode:2017MS & E..267a2036B. Дои:10.1088 / 1757-899X / 267/1/012036.
71. Ведьян, Ахмад; Уолли, Жаклин; Нараянан, Аджит (2017). «Алгоритм гидрологического цикла для задач непрерывной оптимизации». Журнал оптимизации. 2017: 1–25. Дои:10.1155/2017/3828420.
72. Харифи, Сасан; Халилиан, Маджид; Мохаммадзаде, Джавад; Эбрахимнеджад, Садулла (2019). «Колония императорских пингвинов: новый метаэвристический алгоритм оптимизации». Эволюционный интеллект. 12 (2): 211–226. Дои:10.1007 / s12065-019-00212-x.
73. Rawal, A .; Мухопадхьяй, С. (2014). «Прядение синтетических полимерных нитей из расплава». Достижения в производстве текстильных материалов и полимеров из филаментной пряжи. С. 75–99. Дои:10.1533/9780857099174.2.75. ISBN  9780857094995.
74. Zienkiewicz, O.C .; Taylor, R.L .; Фокс, Дэвид (2014). «Нелинейная геометрически точная модель оболочки». Метод конечных элементов для механики твердого тела и конструкций. С. 519–588. Дои:10.1016 / B978-1-85617-634-7.00014-4. ISBN  9781856176347.
75. У, Ю-Шу (2016). «Многофазная жидкость и тепловой поток в сочетании с геомеханикой». Многофазный поток жидкости в пористых и трещиноватых коллекторах. С. 265–293. Дои:10.1016 / B978-0-12-803848-2.00011-8. ISBN  9780128038482.
76. Кавех, Али; Заерреза, Атаолла (2020). «Метод оптимизации с перемешанным пастырем: новый метаэвристический алгоритм». Инженерные вычисления. опережающий печать (опережающий печать): заголовок печати. Дои:10.1108 / EC-10-2019-0481.
77. Зервоудакис, Константинос; Цафаракис, Стелиос (2020). «Алгоритм оптимизации поденок». Компьютеры и промышленная инженерия. опережающий печать (опережающий печать): заголовок печати. Дои:10.1016 / j.cie.2020.106559.
78. Аскари, Камар; Юнас, Ирфан; Саид, Мехрин (2020). «Политический оптимизатор: новая социальная метаэвристика для глобальной оптимизации». Системы, основанные на знаниях. 195: 105709. Дои:10.1016 / j.knosys.2020.105709.
79. Аскари, Камар; Саид, Мехрин; Юнас, Ирфан (2020). «Оптимизатор на основе кучи, вдохновленный корпоративной иерархией рангов для глобальной оптимизации». Экспертные системы с приложениями. 161: 113702. Дои:10.1016 / j.eswa.2020.113702.
80. Чжоу, Цзюй-Шэн; Нгуен, Нгок-Май (2020). «Метаоптимизация, вдохновленная ФБР». Прикладные мягкие вычисления. 93: 106339. Дои:10.1016 / j.asoc.2020.106339 - через Elsevier Science Direct.
81. Чжоу, Цзюй-Шэн; Чыонг, Динь-Нхат (2021 г.). «Новый метаэвристический оптимизатор, вдохновленный поведением медуз в океане». Прикладная математика и вычисления. 389: 125535. Дои:10.1016 / j.amc.2020.125535 - через Elsevier Science Direct.
82. Александр Браунли и Джон Р. Вудворд (2015). «Почему мы разлюбили алгоритмы, вдохновленные природой». Разговор.
83. Джерри Свон, Стивен Адриансен, Мохамед Бишр, Эдмунд К. Берк, Джон А. Кларк, Патрик Де Каусмеккер, Хуанхо Дурилло, Кевин Хаммонд, Эмма Харт, Колин Дж. Джонсон, Золтан А. Кочиш, Бен Ковиц, Кшиштоф Кравец, Саймон Мартин , Дж. Дж. Мерело, Леандро Л. Минку, Эндер Озкан, Жизель Л. Паппа, Эрвин Пеш, Пабло Гаркаа-Санчес, Андреа Шаэрф, Кевин Сим, Джим Э. Смит, Томас Штютцле, Стефан Вос, Стефан Вагнер, Синь Яо. «Программа исследований по метаэвристической стандартизации». «Метафоры часто вдохновляют на новую метаэвристику, но без математической строгости может быть трудно сказать, действительно ли новая метаэвристика отличается от знакомой. Например, математически« поиск гармонии »оказался простым вариантом« поиска гармонии ».Стратегии развития 'хотя метафоры, которые их вдохновляли, были совсем другими. Формальное описание состояния, представления и операторов позволяет отличить подлинную новизну от незначительных вариаций ».
84. Соренсен, Кеннет (2015). «Метаэвристика - метафора разоблачения». Международные операции в операционных исследованиях. 22: 3–18. CiteSeerX  10.1.1.470.3422. Дои:10.1111 / itor.12001.
85. Фред Гловер и Кеннет Соренсен (ред.). «Метаэвристика». Scholarpedia.
86. Журнал эвристической политики исследования эвристического поиска. Springer.
87. «4ИЛИ - включая возможность публикации в открытом доступе».

Рекомендации

• Соренсен, Кеннет; Сево, Марк; Гловер, Фред (2017-01-16). «История метаэвристики» (PDF). В Марти, Рафаэль; Панос, Пардалос; Ресенде, Маурисио (ред.). Справочник эвристики. Springer. ISBN  978-3-319-07123-7.
• Соренсен, Кеннет (2015). «Метаэвристика - метафора разоблачения». Международные операции в операционных исследованиях. 22: 3–18. CiteSeerX  10.1.1.470.3422. Дои:10.1111 / itor.12001.
• Одинокий, Майкл А. (2014). «Метаэвристика в алгоритмах, вдохновленных природой». Материалы конференции 2014 г., компаньон по генетическим и эволюционным вычислениям - GECCO Comp '14. С. 1419–22. CiteSeerX  10.1.1.699.1825. Дои:10.1145/2598394.2609841. ISBN  9781450328814.
• Фистер, Изток; Ян, Синь-Шэ; Фистер, Изток; Брест, Янез; Фистер, Душан (2013). "Краткий обзор вдохновленных природой алгоритмов оптимизации". Электротехники Вестник. 1307 (3): arXiv: 1307.4186. arXiv:1307.4186. Bibcode:2013arXiv1307.4186F.

внешняя ссылка

• Бестиарий эволюционных вычислений - ироничный отчет обо всех странных, даже причудливых метаэвристических методах, существующих в широком мире академических публикаций.
• Список метаэвристических - полный список метаэвристических алгоритмов. Список может быть легко отфильтрован по имени, автору или году и содержит ссылку на основную публикацию каждого алгоритма.