Магнитное квантовое число - Magnetic quantum number

В магнитное квантовое число (символ м_л) является одним из четырех квантовые числа в атомная физика. В наборе есть: главное квантовое число, азимутальное квантовое число, магнитное квантовое число и квантовое число спина. Вместе они описывают уникальное квантовое состояние из электрон. Магнитное квантовое число отличает орбитали доступно в подоболочка, и используется для расчета азимутальной составляющей ориентации орбитали в пространстве. Электроны в определенной подоболочке (например, s, p, d или f) определяются значениями ℓ (0, 1, 2 или 3). Значение м_л может варьироваться от -ℓ к +ℓ, в том числе ноль. Таким образом, подоболочки s, p, d и f содержат 1, 3, 5 и 7 орбиталей каждая со значениями м в пределах 0, ± 1, ± 2, ± 3 соответственно. Каждая из этих орбиталей может вместить до двух электронов (с противоположными спинами), составляющих основу периодическая таблица.

Вывод

Эти орбитали имеют магнитные квантовые числа. ${\displaystyle m=-\ell ,\ldots ,\ell }$ слева направо в порядке возрастания. В ${\displaystyle e^{mi\phi }}$ Зависимость азимутальной составляющей можно увидеть как цветовой градиент, повторяющийся m раз вокруг вертикальной оси.

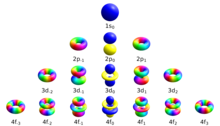
Существует набор квантовых чисел, связанных с энергетическими состояниями атома. Четыре квантовых числа ${\displaystyle n}$, ${\displaystyle \ell }$, ${\displaystyle m_{l}}$, и ${\displaystyle s}$^{[сомнительный ]} указать полную и уникальную квантовое состояние одиночного электрона в атоме называется его волновая функция или же орбитальный. В Уравнение Шредингера для волновой функции атома с одним электроном есть разделимое дифференциальное уравнение в частных производных. (Это не относится к атом гелия или другие атомы с взаимно взаимодействующими электронами, которые требуют более сложных методов для решения^[1]) Это означает, что волновая функция, выраженная в сферические координаты можно разбить на произведение трех функций радиуса, широты (или полярного) угла и азимута:^[2]

${\displaystyle \psi (r,\theta ,\phi )=R(r)P(\theta )F(\phi )}$

Дифференциальное уравнение для ${\displaystyle F}$ можно решить в виде ${\displaystyle F(\phi )=Ae^{\lambda \phi }}$. Поскольку значения азимутального угла ${\displaystyle \phi }$ отличается на 2${\displaystyle \pi }$ (360 градусов в радианы ) представляют собой одно и то же положение в пространстве, а общая величина ${\displaystyle F}$ не растет с произвольно большими ${\displaystyle \phi }$ как и для действительной экспоненты, коэффициент ${\displaystyle \lambda }$ должны быть квантованы до целых кратных ${\displaystyle i}$, производя мнимая экспонента: ${\displaystyle \lambda =im_{l}}$.^[3] Эти целые числа являются магнитными квантовыми числами. Та же самая константа появляется в уравнении ширины, где большие значения ${\displaystyle m_{l}}$² имеют тенденцию уменьшать величину ${\displaystyle P(\theta )}$, а значения ${\displaystyle m_{l}}$ больше, чем азимутальное квантовое число ${\displaystyle \ell }$ не допускают никакого решения для ${\displaystyle P(\theta )}$.

Связь квантовых чисел
Орбитальный	Значения	Количество значений для ${\displaystyle m}$[4]	Электронов на подоболочку
s	${\displaystyle \ell =0,\quad m_{l}=0}$	1	2
п	${\displaystyle \ell =1,\quad m_{l}=-1,0,+1}$	3	6
d	${\displaystyle \ell =2,\quad m_{l}=-2,-1,0,+1,+2}$	5	10
ж	${\displaystyle \ell =3,\quad m_{l}=-3,-2,-1,0,+1,+2,+3}$	7	14
грамм	${\displaystyle \ell =4,\quad m_{l}=-4,-3,-2,-1,0,+1,+2,+3,+4}$	9	18

Как компонент углового момента

Иллюстрация квантово-механического орбитального углового момента. Конусы и плоскость представляют собой возможные ориентации вектора углового момента для ${\displaystyle \ell =2}$ и ${\displaystyle m=-2,-1,0,1,2}$. Даже для экстремальных значений ${\displaystyle m}$, то ${\displaystyle z}$-составляющая этого вектора меньше его суммарной величины.

Ось, используемая для полярных координат в этом анализе, выбрана произвольно. Квантовое число ${\displaystyle m}$ относится к проекции углового момента в этом произвольно выбранном направлении, обычно называемом ${\displaystyle z}$-направление или ось квантования. ${\displaystyle L_{z}}$, величина углового момента в ${\displaystyle z}$-направление, задается формулой:^[4]

${\displaystyle L_{z}=m\hbar }$.

Это составляющая полного орбитального углового момента атомного электрона. ${\displaystyle \mathbf {L} }$, величина которого связана с азимутальным квантовым числом его подоболочки ${\displaystyle \ell }$ уравнением:

${\displaystyle L=\hbar {\sqrt {\ell (\ell +1)}}}$,

куда ${\displaystyle \hbar }$ это приведенная постоянная Планка. Обратите внимание, что это ${\displaystyle L=0}$ за ${\displaystyle \ell =0}$ и приблизительно ${\displaystyle L=\left(\ell +{\tfrac {1}{2}}\right)\hbar }$ для высоких ${\displaystyle \ell }$. Невозможно одновременно измерить угловой момент электрона по всем трем осям. Эти свойства были впервые продемонстрированы в Эксперимент Штерна-Герлаха, к Отто Стерн и Вальтер Герлах.^[5]

Энергия любой волны - это ее частота умноженное на постоянную Планка. Волна отображает частицы, похожие на пакеты энергии, называемые кванты. Формула для квантового числа каждого квантового состояния использует приведенную постоянную Планка, которая допускает только определенные, дискретные или квантованные уровни энергии.^[4]

Эффект в магнитных полях

Квантовое число ${\displaystyle m}$ в общих чертах относится к направлению угловой момент вектор. Магнитное квантовое число ${\displaystyle m}$ влияет только на энергию электрона, если он находится в магнитном поле, потому что в его отсутствие все сферические гармоники, соответствующие различным произвольным значениям ${\displaystyle m}$ эквивалентны. Магнитное квантовое число определяет сдвиг энергии атомная орбиталь из-за внешнего магнитного поля ( Эффект Зеемана ) - отсюда и название магнитный квантовое число. Однако на самом деле магнитный дипольный момент электрона на атомной орбитали приходит не только из углового момента электрона, но и из его спина, выраженного в квантовое число спина.

Поскольку каждый электрон имеет магнитный момент в магнитном поле, на него будет действовать крутящий момент, который стремится заставить вектор ${\displaystyle \mathbf {L} }$ параллельно полю, явление, известное как Ларморова прецессия.

Смотрите также

• Квантовое число
  • Азимутальное квантовое число
  • Главное квантовое число
  • Спиновое квантовое число
  • Квантовое число полного углового момента
• Электронная оболочка
• Основы квантовой механики
• Атом Бора
• Уравнение Шредингера

Рекомендации

1. «Атом гелия». 2010-07-20.
2. «Уравнение Шредингера водорода». hyperphysics.phy-astr.gsu.edu.
3. «Уравнение Шредингера водорода». hyperphysics.phy-astr.gsu.edu.
4. Герцберг, Герхард (1950). Молекулярные спектры и молекулярная структура (2-е изд.). Компания D van Nostrand. С. 17–18.
5. «Спектроскопия: квантовое число углового момента». Encyclopdia Britannica.