Соответствующий фильтр - Matched filter

В обработка сигналов, а согласованный фильтр получается коррелирующий известная задержка сигнал, или же шаблон, с неизвестным сигналом, чтобы обнаружить присутствие шаблона в неизвестном сигнале.^[1][2] Это эквивалентно свертывание неизвестный сигнал с сопряженный версия шаблона с обращенным временем. Соответствующий фильтр является оптимальным линейный фильтр для максимизации соотношение сигнал шум (SNR) в присутствии добавки стохастический шум.

Соответствующие фильтры обычно используются в радар, в котором передается известный сигнал, а отраженный сигнал исследуется на предмет общих элементов выходящего сигнала. Сжатие импульса это пример согласованной фильтрации. Это так называется потому, что импульсный отклик согласован с входными импульсными сигналами. Двумерные согласованные фильтры обычно используются в обработка изображений, например, для улучшения отношения сигнал / шум при рентгеновских наблюдениях. Согласованная фильтрация - это метод демодуляции с LTI (линейный инвариантный во времени) фильтры чтобы максимизировать SNR.^[3]Первоначально он был также известен как Северный фильтр.^[4]

Вывод

Вывод через матричную алгебру

В следующем разделе выводится согласованный фильтр для система с дискретным временем. Вывод для система с непрерывным временем аналогично, с заменой сумм на интегралы.

Согласованный фильтр - это линейный фильтр, ${\displaystyle h}$, что максимизирует выход соотношение сигнал шум.

${\displaystyle \ y[n]=\sum _{k=-\infty }^{\infty }h[n-k]x[k],}$

куда ${\displaystyle x[k]}$ вход как функция независимой переменной ${\displaystyle k}$, и ${\displaystyle y[n]}$ это отфильтрованный вывод. Хотя мы чаще всего выражаем фильтры как импульсивный ответ систем свертки, как указано выше (см. Теория систем LTI ), согласованный фильтр проще всего рассматривать в контексте внутренний продукт, что мы вскоре увидим.

Мы можем получить линейный фильтр, который максимизирует отношение выходного сигнала к шуму, применив геометрический аргумент. Интуиция, лежащая в основе согласованного фильтра, основана на корреляции принятого сигнала (вектора) с фильтром (другим вектором), который параллелен сигналу, максимизируя внутренний продукт. Это усиливает сигнал. Когда мы рассматриваем аддитивный стохастический шум, мы сталкиваемся с дополнительной проблемой минимизировать выходной сигнал из-за шума путем выбора фильтра, ортогонального шуму.

Определим формально проблему. Ищем фильтр, ${\displaystyle h}$, так что мы максимизируем отношение выходного сигнала к шуму, где выходной сигнал является внутренним произведением фильтра и наблюдаемого сигнала ${\displaystyle x}$.

Наш наблюдаемый сигнал состоит из желаемого сигнала ${\displaystyle s}$ и аддитивный шум ${\displaystyle v}$:

${\displaystyle \ x=s+v.\,}$

Определим ковариационная матрица шума, напоминая себе, что эта матрица имеет Эрмитова симметрия, свойство, которое станет полезным при выводе:

${\displaystyle \ R_{v}=E\{vv^{\mathrm {H} }\}\,}$

куда ${\displaystyle v^{\mathrm {H} }}$ обозначает сопряженный транспонировать из ${\displaystyle v}$, и ${\displaystyle E}$ обозначает ожидание. Позвольте нам называть наш вывод, ${\displaystyle y}$, внутренний продукт нашего фильтра и наблюдаемого сигнала, так что

${\displaystyle \ y=\sum _{k=-\infty }^{\infty }h^{*}[k]x[k]=h^{\mathrm {H} }x=h^{\mathrm {H} }s+h^{\mathrm {H} }v=y_{s}+y_{v}.}$

Теперь мы определяем отношение сигнал / шум, которое является нашей целевой функцией, как отношение выходной мощности из-за полезного сигнала к выходной мощности из-за шума:

${\displaystyle \mathrm {SNR} ={\frac {|y_{s}|^{2}}{E\{|y_{v}|^{2}\}}}.}$

Перепишем вышесказанное:

${\displaystyle \mathrm {SNR} ={\frac {|h^{\mathrm {H} }s|^{2}}{E\{|h^{\mathrm {H} }v|^{2}\}}}.}$

Мы хотим максимально увеличить это количество, выбрав ${\displaystyle h}$. Раскладывая знаменатель нашей целевой функции, мы имеем

${\displaystyle \ E\{|h^{\mathrm {H} }v|^{2}\}=E\{(h^{\mathrm {H} }v){(h^{\mathrm {H} }v)}^{\mathrm {H} }\}=h^{\mathrm {H} }E\{vv^{\mathrm {H} }\}h=h^{\mathrm {H} }R_{v}h.\,}$

Теперь наш ${\displaystyle \mathrm {SNR} }$ становится

${\displaystyle \mathrm {SNR} ={\frac {|h^{\mathrm {H} }s|^{2}}{h^{\mathrm {H} }R_{v}h}}.}$

Мы перепишем это выражение, изменив матрицу. Причина этой, казалось бы, контрпродуктивной меры станет очевидной в ближайшее время. Использование эрмитовой симметрии ковариационной матрицы ${\displaystyle R_{v}}$, мы можем написать

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}},}$

Мы хотели бы найти верхнюю границу этого выражения. Для этого мы сначала распознаем форму Неравенство Коши – Шварца:

${\displaystyle \ |a^{\mathrm {H} }b|^{2}\leq (a^{\mathrm {H} }a)(b^{\mathrm {H} }b),\,}$

это означает, что квадрат внутреннего произведения двух векторов может быть только таким большим, как произведение отдельных внутренних произведений векторов. Эта концепция возвращается к интуиции, лежащей в основе согласованного фильтра: эта верхняя граница достигается, когда два вектора ${\displaystyle a}$ и ${\displaystyle b}$ параллельны. Мы возобновляем наш вывод, выражая верхнюю границу нашего ${\displaystyle \mathrm {SNR} }$ в свете геометрического неравенства выше:

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq {\frac {\left[{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)\right]\left[{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)\right]}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}.}$

Наши отважные манипуляции с матрицей теперь окупились. Мы видим, что выражение для нашей верхней границы можно значительно упростить:

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq s^{\mathrm {H} }R_{v}^{-1}s.}$

Мы можем достичь этой верхней границы, если выберем

${\displaystyle \ R_{v}^{1/2}h=\alpha R_{v}^{-1/2}s}$

куда ${\displaystyle \alpha }$ - произвольное действительное число. Чтобы проверить это, мы подключаемся к нашему выражению для вывода ${\displaystyle \mathrm {SNR} }$:

${\displaystyle \mathrm {SNR} ={\frac {|{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}={\frac {\alpha ^{2}|{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)|^{2}}{\alpha ^{2}{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)}}={\frac {|s^{\mathrm {H} }R_{v}^{-1}s|^{2}}{s^{\mathrm {H} }R_{v}^{-1}s}}=s^{\mathrm {H} }R_{v}^{-1}s.}$

Таким образом, наш оптимальный согласованный фильтр

${\displaystyle \ h=\alpha R_{v}^{-1}s.}$

Мы часто предпочитаем нормализовать ожидаемое значение мощности на выходе фильтра из-за шума до единицы. То есть мы сдерживаем

${\displaystyle \ E\{|y_{v}|^{2}\}=1.\,}$

Это ограничение подразумевает значение ${\displaystyle \alpha }$, для которого мы можем решить:

${\displaystyle \ E\{|y_{v}|^{2}\}=\alpha ^{2}s^{\mathrm {H} }R_{v}^{-1}s=1,}$

уступающий

${\displaystyle \ \alpha ={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}},}$

давая нам нормализованный фильтр,

${\displaystyle \ h={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}}R_{v}^{-1}s.}$

Если мы хотим написать импульсную характеристику ${\displaystyle h}$ фильтра для системы свертки, это просто комплексно-сопряженное обращение времени входного ${\displaystyle s}$.

Хотя мы получили согласованный фильтр в дискретном времени, мы можем расширить эту концепцию на системы с непрерывным временем, если заменим ${\displaystyle R_{v}}$ с непрерывным временем автокорреляция функция шума, предполагая непрерывный сигнал ${\displaystyle s(t)}$, непрерывный шум ${\displaystyle v(t)}$, и непрерывный фильтр ${\displaystyle h(t)}$.

Вывод через лагранжиан

В качестве альтернативы мы можем найти согласованный фильтр, решив нашу задачу максимизации с помощью лагранжиана. И снова согласованный фильтр стремится максимизировать отношение выходного сигнала к шуму (${\displaystyle \mathrm {SNR} }$) отфильтрованного детерминированного сигнала в стохастическом аддитивном шуме. Наблюдаемая последовательность опять же

${\displaystyle \ x=s+v,\,}$

с ковариационной матрицей шума,

${\displaystyle \ R_{v}=E\{vv^{\mathrm {H} }\}.\,}$

Отношение сигнал / шум равно

${\displaystyle \mathrm {SNR} ={\frac {|y_{s}|^{2}}{E\{|y_{v}|^{2}\}}}.}$

Вычисляя выражение в числителе, имеем

${\displaystyle \ |y_{s}|^{2}={y_{s}}^{\mathrm {H} }y_{s}=h^{\mathrm {H} }ss^{\mathrm {H} }h.\,}$

а в знаменателе

${\displaystyle \ E\{|y_{v}|^{2}\}=E\{{y_{v}}^{\mathrm {H} }y_{v}\}=E\{h^{\mathrm {H} }vv^{\mathrm {H} }h\}=h^{\mathrm {H} }R_{v}h.\,}$

Отношение сигнал / шум становится

${\displaystyle \mathrm {SNR} ={\frac {h^{\mathrm {H} }ss^{\mathrm {H} }h}{h^{\mathrm {H} }R_{v}h}}.}$

Если теперь ограничить знаменатель равным 1, проблема максимизации ${\displaystyle \mathrm {SNR} }$ сводится к максимальному числителю. Затем мы можем сформулировать проблему, используя Множитель Лагранжа:

${\displaystyle \ h^{\mathrm {H} }R_{v}h=1}$

${\displaystyle \ {\mathcal {L}}=h^{\mathrm {H} }ss^{\mathrm {H} }h+\lambda (1-h^{\mathrm {H} }R_{v}h)}$

${\displaystyle \ \nabla _{h^{*}}{\mathcal {L}}=ss^{\mathrm {H} }h-\lambda R_{v}h=0}$

${\displaystyle \ (ss^{\mathrm {H} })h=\lambda R_{v}h}$

который мы признаем обобщенная задача на собственные значения

${\displaystyle \ h^{\mathrm {H} }(ss^{\mathrm {H} })h=\lambda h^{\mathrm {H} }R_{v}h.}$

С ${\displaystyle ss^{\mathrm {H} }}$ имеет единичный ранг, у него только одно ненулевое собственное значение. Можно показать, что это собственное значение равно

${\displaystyle \ \lambda _{\max }=s^{\mathrm {H} }R_{v}^{-1}s,}$

давая следующий оптимальный согласованный фильтр

${\displaystyle \ h={\frac {1}{\sqrt {s^{\mathrm {H} }R_{v}^{-1}s}}}R_{v}^{-1}s.}$

Это тот же результат, что и в предыдущем подразделе.

Интерпретация оценки методом наименьших квадратов

Согласованную фильтрацию также можно интерпретировать как оценку методом наименьших квадратов для оптимального расположения и масштабирования данной модели или шаблона. Еще раз, пусть наблюдаемая последовательность определяется как

${\displaystyle \ x_{k}=s_{k}+v_{k},\,}$

куда ${\displaystyle v_{k}}$ - это некоррелированный шум с нулевым средним. Сигнал ${\displaystyle s_{k}}$ предполагается, что это масштабированная и сдвинутая версия известной модельной последовательности ${\displaystyle f_{k}}$:

${\displaystyle \ s_{k}=\mu _{0}\cdot f_{k-j_{0}}}$

Мы хотим найти оптимальные оценки ${\displaystyle j^{*}}$ и ${\displaystyle \mu ^{*}}$ для неизвестной смены ${\displaystyle j_{0}}$ и масштабирование ${\displaystyle \mu _{0}}$ путем минимизации остатка наименьших квадратов между наблюдаемой последовательностью ${\displaystyle x_{k}}$ и «зондирующая последовательность» ${\displaystyle h_{j-k}}$:

${\displaystyle \ j^{*},\mu ^{*}=\arg \min _{j,\mu }\sum _{k}\left(x_{k}-\mu \cdot h_{j-k}\right)^{2}}$

Соответствующий ${\displaystyle h_{j-k}}$ позже окажется согласованным фильтром, но пока не определен. Расширение ${\displaystyle x_{k}}$ а квадрат в сумме дает

${\displaystyle \ j^{*},\mu ^{*}=\arg \min _{j,\mu }\left[\sum _{k}(s_{k}+v_{k})^{2}+\mu ^{2}\sum _{k}h_{j-k}^{2}-2\mu \sum _{k}s_{k}h_{j-k}-2\mu \sum _{k}v_{k}h_{j-k}\right]}$.

Первый член в скобках является константой (поскольку дается наблюдаемый сигнал) и не влияет на оптимальное решение. Последний член имеет постоянное ожидаемое значение, потому что шум не коррелирован и имеет нулевое среднее. Таким образом, мы можем исключить оба термина из оптимизации. Меняя знак, получаем эквивалентную задачу оптимизации

${\displaystyle \ j^{*},\mu ^{*}=\arg \max _{j,\mu }\left[2\mu \sum _{k}s_{k}h_{j-k}-\mu ^{2}\sum _{k}h_{j-k}^{2}\right]}$.

Установка производной по w.r.t. ${\displaystyle \mu }$ к нулю дает аналитическое решение для ${\displaystyle \mu ^{*}}$:

${\displaystyle \ \mu ^{*}={\frac {\sum _{k}s_{k}h_{j-k}}{\sum _{k}h_{j-k}^{2}}}}$.

Вставка этого в нашу целевую функцию дает сокращенную задачу максимизации всего за ${\displaystyle j^{*}}$:

${\displaystyle \ j^{*}=\arg \max _{j}{\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}}$.

Числитель может быть ограничен сверху с помощью Неравенство Коши – Шварца:

${\displaystyle \ {\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}\leq {\frac {\sum _{k}s_{k}^{2}\cdot \sum _{k}h_{j-k}^{2}}{\sum _{k}h_{j-k}^{2}}}=\sum _{k}s_{k}^{2}=\mathrm {const} }$.

Задача оптимизации принимает максимум, когда в этом выражении выполняется равенство. Согласно свойствам неравенства Коши – Шварца это возможно только при

${\displaystyle \ h_{j-k}=\nu \cdot s_{k}=\kappa \cdot f_{k-j_{0}}}$.

для произвольных ненулевых констант ${\displaystyle \nu }$ или же ${\displaystyle \kappa }$, а оптимальное решение получается при ${\displaystyle j^{*}=j_{0}}$ по желанию. Таким образом, наша «последовательность зондирования» ${\displaystyle h_{j-k}}$ должен быть пропорционален модели сигнала ${\displaystyle f_{k-j_{0}}}$, и удобный выбор ${\displaystyle \kappa =1}$ дает согласованный фильтр

${\displaystyle \ h_{k}=f_{-k}}$.

Обратите внимание, что фильтр является зеркальной моделью сигнала. Это гарантирует, что операция ${\displaystyle \sum _{k}x_{k}h_{j-k}}$ чтобы найти оптимум, действительно, свертка между наблюдаемой последовательностью ${\displaystyle x_{k}}$ и согласованный фильтр ${\displaystyle h_{k}}$. Отфильтрованная последовательность принимает максимум в том месте, где наблюдаемая последовательность ${\displaystyle x_{k}}$ наилучшее соответствие (в смысле наименьших квадратов) модели сигнала ${\displaystyle f_{k}}$.

Подразумеваемое

Согласованный фильтр может быть получен различными способами,^[2] но как частный случай процедура наименьших квадратов это также можно интерпретировать как максимальная вероятность метод в контексте (цветного) Гауссов шум модель и связанные Малая вероятность.^[5]Если передаваемый сигнал обладал нет неизвестные параметры (например, время прихода, амплитуда, ...), то согласованный фильтр, в соответствии с Лемма Неймана – Пирсона., минимизируйте вероятность ошибки. Однако, поскольку точный сигнал обычно определяется неизвестными параметрами, которые эффективно оцениваются (или приспособленный) в процессе фильтрации согласованный фильтр представляет собой обобщенное максимальное правдоподобие (тестовая) статистика.^[6] Отфильтрованные временные ряды затем можно интерпретировать как (пропорционально) вероятность профиля, максимальное условное правдоподобие как функция параметра времени.^[7]Это, в частности, означает, что вероятность ошибки (в смысле Неймана и Пирсона, т. е. относительно максимизации вероятности обнаружения для данной вероятности ложной тревоги^[8]) не обязательно является оптимальным. Отношение сигнал / шум (SNR), который должен быть максимизирован согласованным фильтром, в этом контексте соответствует ${\displaystyle {\sqrt {2\log({\mathcal {L}})}}}$, куда ${\displaystyle {\mathcal {L}}}$ является (условно) максимальным отношением правдоподобия.^{[7] [nb 1]}

Конструкция согласованного фильтра основана на известен спектр шума. В действительности же спектр шума обычно по оценкам из данных и, следовательно, известны только с ограниченной точностью. Для случая неопределенного спектра согласованный фильтр может быть обобщен до более надежной итерационной процедуры с благоприятными свойствами также в негауссовском шуме.^[7]

Интерпретация в частотной области

При рассмотрении в частотной области очевидно, что согласованный фильтр применяет наибольшее взвешивание к спектральным компонентам, демонстрирующим наибольшее отношение сигнал / шум (т. Е. Большой вес при относительно низком уровне шума, и наоборот). Как правило, для этого требуется неплоская частотная характеристика, но связанные с этим "искажения" не вызывают беспокойства в таких ситуациях, как радар и цифровые коммуникации, где исходная форма сигнала известна, и целью является обнаружение этого сигнала на фоне фонового шума. С технической стороны подобранный фильтр представляет собой взвешенный метод наименьших квадратов метод, основанный на (гетероскедастический ) данные частотной области (где «веса» определяются через спектр шума, см. также предыдущий раздел) или, что то же самое, наименьших квадратов метод применяется к побеленный данные.

Примеры

Согласованный фильтр в радаре и сонаре

Соответствующие фильтры часто используются в обнаружение сигнала.^[1] В качестве примера предположим, что мы хотим судить о расстоянии до объекта, отражая от него сигнал. Мы можем выбрать передачу синусоиды чистого тона с частотой 1 Гц. Мы предполагаем, что наш принятый сигнал представляет собой ослабленную и сдвинутую по фазе форму переданного сигнала с добавленным шумом.

Чтобы судить о расстоянии до объекта, мы коррелируем полученный сигнал с согласованным фильтром, который в случае белый (некоррелированный) шум, это еще одна синусоида с чистым тоном 1 Гц. Когда выходной сигнал системы согласованного фильтра превышает определенный порог, мы с высокой вероятностью заключаем, что принятый сигнал был отражен от объекта. Используя скорость распространения и время, в которое мы впервые наблюдаем отраженный сигнал, мы можем оценить расстояние до объекта. Если мы изменим форму импульса специально разработанным способом, отношение сигнал / шум и разрешение по расстоянию можно будет даже улучшить после согласованной фильтрации: это метод, известный как сжатие импульса.

Кроме того, согласованные фильтры могут использоваться в задачах оценки параметров (см. теория оценки ). Чтобы вернуться к нашему предыдущему примеру, мы можем захотеть оценить скорость объекта в дополнение к его положению. Чтобы использовать Эффект Допплера, мы хотим оценить частоту принимаемого сигнала. Для этого мы можем коррелировать принятый сигнал с несколькими согласованными фильтрами синусоид на различных частотах. Согласованный фильтр с максимальным выходным сигналом с большой вероятностью обнаружит частоту отраженного сигнала и поможет нам определить скорость объекта. Фактически, этот метод является простой версией дискретное преобразование Фурье (ДПФ). ДПФ занимает ${\displaystyle N}$-значный комплексный ввод и соотносит его с ${\displaystyle N}$ согласованные фильтры, соответствующие комплексным экспонентам при ${\displaystyle N}$ разные частоты, чтобы дать ${\displaystyle N}$ комплексные числа, соответствующие относительным амплитудам и фазам синусоидальных составляющих (см. Индикация движущейся цели ).

Согласованный фильтр в цифровой связи

Согласованный фильтр также используется в коммуникациях. В контексте системы связи, которая отправляет двоичные сообщения от передатчика к приемнику по зашумленному каналу, согласованный фильтр может использоваться для обнаружения переданных импульсов в зашумленном принятом сигнале.

Представьте, что мы хотим отправить последовательность «0101100100», закодированную в неполярном Невозврат к нулю (NRZ) через определенный канал.

Математически последовательность в коде NRZ может быть описана как последовательность единичных импульсов или сдвинутых прямые функции, каждый импульс взвешивается на +1, если бит равен «1», и на -1, если бит равен «0». Формально коэффициент масштабирования для ${\displaystyle k^{\mathrm {th} }}$ немного,

${\displaystyle \ a_{k}={\begin{cases}+1,&{\mbox{if bit }}k{\mbox{ is 1}},\\-1,&{\mbox{if bit }}k{\mbox{ is 0}}.\end{cases}}}$

Мы можем представить наше сообщение, ${\displaystyle M(t)}$, как сумма сдвинутых единичных импульсов:

${\displaystyle \ M(t)=\sum _{k=-\infty }^{\infty }a_{k}\times \Pi \left({\frac {t-kT}{T}}\right).}$

куда ${\displaystyle T}$ длина одного бита.

Таким образом, сигнал, который должен послать передатчик,

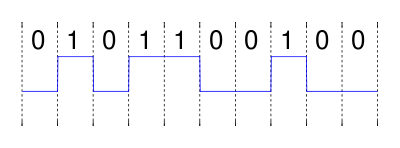
Если мы смоделируем наш шумный канал как AWGN канал, к сигналу добавляется белый гауссов шум. На стороне приемника для отношения сигнал / шум 3 дБ это может выглядеть так:

Первый взгляд не покажет исходную переданную последовательность. Имеется высокая мощность шума относительно мощности полезного сигнала (т. Е. Низкая соотношение сигнал шум ). Если бы приемник отбирал этот сигнал в правильные моменты, результирующее двоичное сообщение могло бы противоречить исходному переданному.

Чтобы увеличить отношение сигнал / шум, мы пропускаем полученный сигнал через согласованный фильтр. В этом случае фильтр должен быть согласован с импульсом NRZ (эквивалентным «1», закодированной в коде NRZ). Точнее, импульсная характеристика идеального согласованного фильтра, предполагающая белый (некоррелированный) шум, должна быть масштабированной комплексно-сопряженной версией сигнала, который мы ищем, с обращенной во времени. Мы выбрали

${\displaystyle \ h(t)=\Pi \left({\frac {t}{T}}\right).}$

В этом случае из-за симметрии обращенное во времени комплексное сопряжение ${\displaystyle h(t)}$ на самом деле ${\displaystyle h(t)}$, что позволяет нам звонить ${\displaystyle h(t)}$ импульсная характеристика нашей системы свертки согласованных фильтров.

После свертки с правильным согласованным фильтром результирующий сигнал, ${\displaystyle M_{\mathrm {filtered} }(t)}$ является,

${\displaystyle \ M_{\mathrm {filtered} }(t)=M(t)*h(t)}$

куда ${\displaystyle *}$ обозначает свертку.

Который теперь может быть безопасно выбран приемником в правильные моменты выборки и сравнен с соответствующим порогом, что приводит к правильной интерпретации двоичного сообщения.

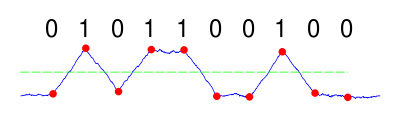
Согласованный фильтр в гравитационно-волновой астрономии

Соответствующие фильтры играют центральную роль в гравитационно-волновая астрономия.^[9] В первое наблюдение гравитационных волн был основан на крупномасштабной фильтрации выходного сигнала каждого детектора для сигналов, напоминающих ожидаемую форму, с последующим скринингом на совпадение и когерентность запуска между обоими приборами. Частота ложных тревог, и с этим Статистическая значимость обнаружения затем оценивали с помощью повторная выборка методы.^[10][11] Вывод о параметрах астрофизического источника был выполнен с использованием Байесовские методы на основе параметризованных теоретических моделей формы сигнала и (опять же) Малая вероятность.^[12][13]

Смотрите также

• Периодограмма
• Отфильтрованная обратная проекция (Преобразование Радона)
• Цифровой фильтр
• Статистическая обработка сигналов
• Малая вероятность
• Вероятность профиля
• Теория обнаружения
• Проблема множественных сравнений
• Емкость канала
• Теорема кодирования с шумом
• Оценка спектральной плотности
• Фильтр наименьших средних квадратов (LMS)
• Винеровский фильтр
• МНОЖЕСТВЕННАЯ СИГНАЛЬНАЯ КЛАССИФИКАЦИЯ (МУЗЫКА), популярный параметрический сверхразрешение метод
• САМВ

Примечания

1. Общая ссылка на SNR на самом деле был раскритикован как несколько вводящий в заблуждение: "Интересной особенностью этого подхода является то, что теоретическое совершенство достигается без сознательного стремления к максимальному соотношению сигнал / шум. Что представляет собой весьма случайный интерес, случается, что операция [...] действительно увеличивает пиковое отношение сигнал / шум, но этот факт не играет никакой роли в настоящей теории. Отношение сигнал / шум не является показателем информации [...]." (Woodward, 1953;^[1] Раздел 5.1).

Рекомендации

1. Woodward, П. М. (1953). Теория вероятностей и информации с приложениями к радарам. Лондон: Pergamon Press.
2. Турин, Г. Л. (1960). «Введение в согласованные фильтры». Сделки IRE по теории информации. 6 (3): 311–329. Дои:10.1109 / TIT.1960.1057571.
3. «Демодуляция». OpenStax CNX. Получено 2017-04-18.
4. После Д.О. Норт, который одним из первых представил концепцию: Норт, Д. О. (1943). «Анализ факторов, определяющих дискриминацию сигнал / шум в импульсных системах несущей». Отчет PPR-6C, RCA Laboratories, Принстон, Нью-Джерси.
   Повторная печать: Норт, Д. О. (1963). «Анализ факторов, определяющих дискриминацию сигнал / шум в системах с импульсной несущей». Труды IEEE. 51 (7): 1016–1027. Дои:10.1109 / PROC.1963.2383.
   Смотрите также: Джейнс, Э. Т. (2003). «14.6.1 Классический согласованный фильтр". Теория вероятностей: логика науки. Кембридж: Издательство Кембриджского университета.
5. Choudhuri, N .; Ghosal, S .; Рой, А. (2004). «Примыкание меры Уиттла для гауссовского временного ряда». Биометрика. 91 (4): 211–218. Дои:10.1093 / biomet / 91.1.211.
6. Настроение, А. М .; Graybill, F.A .; Бос, Д. К. (1974). «IX. Проверка гипотез". Введение в теорию статистики (3-е изд.). Нью-Йорк: Макгроу-Хилл.
7. Рёвер, К. (2011). «Фильтр Стьюдента для надежного обнаружения сигнала». Физический обзор D. 84 (12): 122004. arXiv:1109.0442. Bibcode:2011ПхРвД..84л2004Р. Дои:10.1103 / PhysRevD.84.122004.
8. Neyman, J .; Пирсон, Э. С. (1933). «К вопросу о наиболее эффективных проверках статистических гипотез». Философские труды Лондонского королевского общества A. 231 (694–706): 289–337. Bibcode:1933РСПТА.231..289Н. Дои:10.1098 / рста.1933.0009.
9. Шютц, Б. Ф. (1999). «Гравитационно-волновая астрономия». Классическая и квантовая гравитация. 16 (12A): A131 – A156. arXiv:gr-qc / 9911034. Bibcode:1999CQGra..16A.131S. Дои:10.1088 / 0264-9381 / 16 / 12A / 307.
10. Усман, Саманта А. (2016). «Поиск в PyCBC гравитационных волн от слияния компактных двойников». Учебный класс. Квантовая гравитация. 33: 215004. arXiv:1508.02357. Bibcode:2016CQGra..33u5004U. Дои:10.1088/0264-9381/33/21/215004.
11. Abbott, B.P .; и другие. (Научное сотрудничество LIGO, Сотрудничество Девы) (2016). «GW150914: Первые результаты поиска слияния двойных черных дыр с помощью Advanced LIGO». Физический обзор D. 93: 122003. arXiv:1602.03839. Bibcode:2016ПхРвД..93л2003А. Дои:10.1103 / PhysRevD.93.122003.
12. Abbott, B.P .; и другие. (Научное сотрудничество LIGO, Сотрудничество Девы) (2016). "Свойства двойного слияния черных дыр GW150914". Письма с физическими проверками. 116: 241102. arXiv:1602.03840. Bibcode:2016ПхРвЛ.116х1102А. Дои:10.1103 / PhysRevLett.116.241102. PMID  27367378.
13. Meyer, R .; Кристенсен, Н. (2016). «Гравитационные волны: статистическое вскрытие слияния черных дыр». Значимость. 13 (2): 20–25. Дои:10.1111 / j.1740-9713.2016.00896.x.

дальнейшее чтение

• Турин, Г. Л. (1960). «Введение в согласованные фильтры». Сделки IRE по теории информации. 6 (3): 311–329. Дои:10.1109 / TIT.1960.1057571.
• Wainstein, L.A .; Зубаков, В. Д. (1962). Извлечение сигналов из шума. Энглвуд Клиффс, Нью-Джерси: Prentice-Hall.
• Мелвин, У. Л. (2004). «Обзор STAP». Журнал IEEE Aerospace and Electronic Systems Magazine. 19 (1): 19–35. Дои:10.1109 / MAES.2004.1263229.
• Рёвер, К. (2011). «Фильтр Стьюдента для надежного обнаружения сигнала». Физический обзор D. 84 (12): 122004. arXiv:1109.0442. Bibcode:2011ПхРвД..84л2004Р. Дои:10.1103 / PhysRevD.84.122004.
• Fish, A .; Гуревич, С .; Hadani, R .; Sayeed, A .; Шварц, О. (декабрь 2011 г.). «Вычисление согласованного фильтра за линейное время». arXiv:1112.4883 [cs.IT ].