Подвижный клеточный автомат - Movable cellular automaton

Метод подвижного клеточного автомата

Анимация подвижного клеточного автомата, используемого для моделирования трение на границе между двумя поверхностями
Тип метода
Непрерывный / Дискретный	Дискретный
Аналитический / вычислительный	Вычислительная
Характеристики
Под влиянием	клеточный автомат, дискретный элемент
Метод в	вычислительная механика твердого тела

В метод подвижного клеточного автомата (MCA) это метод в вычислительная механика твердого тела на основе дискретной концепции. Это дает преимущества как классических клеточный автомат и дискретный элемент методы. Одно важное преимущество^{[нужна цитата ]} метода MCA заключается в том, что он позволяет симуляция разрушения материала, включая образование повреждений, распространение трещин, фрагментацию и перемешивание массы. Эти процессы сложно смоделировать с помощью механика сплошной среды методы (например: метод конечных элементов, метод конечных разностей и т. д.), поэтому некоторые новые концепции, такие как перидинамика необходимы. Метод дискретных элементов очень эффективен для моделирования сыпучих материалов, но взаимные силы между подвижными клеточными автоматами позволяют моделировать поведение твердых тел. Когда размер ячейки автомата приближается к нулю, поведение MCA приближается к классическому. механика сплошной среды методы.^{[нужна цитата ]}

Краеугольный камень метода подвижного клеточного автомата

Объект (слева) описан как набор взаимодействующих автоматов (в центре). Справа показано поле скоростей автоматов.

В рамках MCA При приближении моделируемый объект рассматривается как совокупность взаимодействующих элементов / автоматов. Динамика множества автоматов определяется их взаимными силами и правилами их взаимоотношений. Эта система существует и действует во времени и пространстве. Его эволюция во времени и пространстве регулируется уравнениями движения. Взаимные силы и правила межэлементных взаимоотношений определяются функцией реакции автомата. Эта функция должна быть указана для каждого автомата. В связи с мобильностью автоматов необходимо учитывать следующие новые параметры клеточных автоматов: р^я - радиус-вектор автомата; V^я - скорость автомата; ω^я - скорость вращения автомата; θ^я - вектор вращения автомата; м^я - масса автомата; J^я - момент инерции автомата.

Новая концепция: соседи

У каждого автомата есть соседи

Новая концепция метода MCA основана на введении состояние пары автоматов (отношение взаимодействующих пар автоматов) в дополнение к условному - состояние отдельного автомата. Обратите внимание, что введение этого определения позволяет перейти от концепции статической сети к концепции концепция соседей. В результате у автоматов появляется возможность менять своих соседей, переключая состояния (отношения) пар.

Определение параметра состояния пары

Введение нового типа состояний приводит к появлению нового параметра для использования его в качестве критерия для переключение отношений. Он определяется как автомат перекрытия параметровчас^ij. Таким образом, взаимоотношения клеточных автоматов характеризуются величиной их перекрытие.

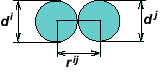
Начальная структура формируется путем установления определенных отношений между каждой парой соседних элементов.

Критерий переключения состояния парных отношений

Слева зацеплена пара автоматов ij. Правая пара автоматов ij не связана.

В отличие от классического метода клеточного автомата в методе МКА не только один автомат, но и отношения пары автоматов можно переключать. Согласно концепции бистабильных автоматов существует два типа парных состояний (отношений):

связаны	- оба автомата принадлежат твердому
несвязанный	- каждый автомат пары принадлежит разным телам или частям поврежденного тела.

Итак изменение состояния парных отношений управляется относительными движениями автоматов, и среды, образованные такими парами, можно рассматривать как бистабильные среды.

Уравнения движения МКА

Эволюция среды MCA описывается следующими уравнения движения для перевода:

${\displaystyle {d^{2}h^{ij} \over dt^{2}}=\left({1 \over m^{i}}+{1 \over m^{j}}\right)p^{ij}+\sum _{k\neq j}C(ij,ik)\psi (\alpha _{ij,ik}){1 \over m^{i}}p^{ik}+\sum _{l\neq i}C(ij,jl)\psi (\alpha _{ij,jl}){1 \over m^{j}}p^{jl}}$

Силы между автоматами ij исходят от их соседей.

Здесь m^я масса автомата i, p^ij - центральная сила, действующая между автоматами i и j, C (ij, ik) - некоторый коэффициент, связанный с передачей параметра h из пары ij в пару ik, ψ (α_{ij, ik}) угол между направлениями ij и ik.

Из-за конечных размеров подвижных автоматов необходимо учитывать эффекты вращения. В уравнения движения для вращения можно записать так:

${\displaystyle {d^{2}\theta ^{ij} \over dt^{2}}=\left({q^{ij} \over J^{i}}+{q^{ji} \over J^{j}}\right)\tau ^{ij}+\sum _{k\neq j}S(ij,ik){q^{ik} \over J^{i}}\tau ^{ik}+\sum _{l\neq j}S(ij,jl){q^{jl} \over J^{j}}\tau ^{jl}}$

Здесь Θ^ij - угол относительного поворота (это параметр переключения, такой как h^ij для перевода), q^ij это расстояние от центра автомата я к точке связи автомата j (плечо момента), τ^ij - парное тангенциальное взаимодействие, S (ij, ik) - некоторый коэффициент, связанный с переносом параметра Θ из одной пары в другую (аналогично C (ij, ik) из уравнения для переноса).

Эти уравнения полностью аналогичны уравнениям движения для многочастичного подхода.

Определение деформации в паре автоматов

Вращение тела в целом, не приводящее к деформации в паре автоматов

Перевод парных автоматовБезразмерный параметр деформации для перевода я j Пара автоматов может быть представлена ​​как:

${\displaystyle \varepsilon ^{ij}={h^{ij} \over r_{0}^{ij}}={\left(q^{ij}+q^{ji}\right)-\left(d^{i}+d^{j}\right){\big /}2 \over \left(d^{i}+d^{j}\right){\big /}2}}$

В этом случае:

${\displaystyle \left(\Delta {\varepsilon ^{i(j)}}+\Delta {\varepsilon ^{j(i)}}\right){\left(d^{i}+d^{j}\right) \over 2}=V_{n}^{ij}\Delta {t}}$

куда Δt шаг времени, V_п^ij - относительная скорость.

Вращение парных автоматов можно рассчитать по аналогии с последними трансляционными соотношениями.

Моделирование необратимой деформации методом MCA

Деформация определяется величиной расстояния от центра автомата.

Существует два типа функции отклика автоматов.

В ε^ij параметр используется как мера деформации автомата я при его взаимодействии с автоматом j. Где q^ij - расстояние от центра автомата я к точке контакта с автоматом j; р^я = d^я/2 (d^я - размер автомата я).

Например рассматривается образец титана при циклическом нагружении (растяжение - сжатие). Схема загрузки показана на следующем рисунке:

Схема загрузки	Схема загрузки
	(Красные метки экспериментальные данные)

Преимущества метода MCA

Благодаря мобильности каждого автомата метод MCA позволяет напрямую учитывать такие действия, как:

• смешивание масс
• эффекты проникновения
• химические реакции
• интенсивная деформация
• фазовые превращения
• накопление убытков
• фрагментация и перелом
• образование и развитие трещин

Используя граничные условия разных типов (фиксированные, упругие, вязкоупругие и др.), Можно имитировать различные свойства окружающей среды, содержащей моделируемую систему. Можно моделировать различные режимы механического нагружения (растяжение, сжатие, деформация сдвига и т. Д.), Задав дополнительные условия на границах.

Смотрите также

• Механика сплошной среды - Раздел механики, который занимается анализом кинематики и механического поведения материалов, моделируемых как непрерывная масса, а не как дискретные частицы
• Механика твердого тела - Раздел механики, связанный с твердыми материалами и их поведением
• Механика разрушения - Область механики, связанная с изучением распространения трещин в материалах
• Перидинамика
• Компьютерное моделирование - Процесс математического моделирования, выполняемый на компьютере
• Метод дискретных элементов - Численные методы расчета движения и воздействия большого количества мелких частиц
• Клеточный автомат - Дискретная модель, изучаемая в информатике
• Метод конечных элементов - Численный метод решения физических или инженерных задач
• Метод конечных разностей

Рекомендации

• Псахие, С.Г .; Horie, Y .; Коростелев, С.Ю .; Смолин, А.Ю .; Дмитриев, А.И .; Шилко, Е.В .; Алексеев, С.В. (Ноябрь 1995 г.). «Метод подвижных клеточных автоматов как инструмент моделирования в рамках мезомеханики». Российский физический журнал. 38 (11): 1157–1168. Дои:10.1007 / BF00559396.
• Псахие, С.Г .; Коростелев, С.Ю .; Смолин, А.Ю .; Дмитриев, А.И .; Шилко, Е.В .; Моисеенко Д.Д .; Татаринцев Э.М.; Алексеев, С.В. (1998). «Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов». Физическая мезомеханика. 1 (1): 95–108. (Псахье, С.Г .; Коростелев, С.Ю .; Смолин, А.Ю .; Дмитриев, А.И .; Шилько, Е.В .; Моисеенко, Д.Д .; Татаринцев, Е.М .; Алексеев, С.В. (1998). "Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов". Физическая мезомеханика. 1 (1): 95–108. Получено 2010-03-03.)
• Псахие, С.Г .; Ostermeyer, G.P .; Дмитриев, А.И .; Шилко, Е.В .; Смолин, А.Ю .; Коростелев, С. (2000). «Метод подвижных клеточных автоматов как новое направление в численной дискретной механике. I. Теоретическое описание». Физическая мезомеханика. 3 (2): 5–13. (Псахье, С.Г .; Остермайер, Г.П .; Дмитриев, А.И .; Шилько, Е.В .; Смолин, А.Ю .; Коростелев, С.Ю. (2000). "Метод подвижных клеточных автоматов как новое направление дискретной вычислительной механики. I. Теоретическое описание". Физическая мезомеханика. 3 (2): 5–13. Получено 2010-03-03.)
• Псахие, С.Г .; Horie, Y .; Ostermeyer, G.P .; Коростелев, С.Ю .; Смолин, А.Ю .; Шилко, Е.В .; Дмитриев, А.И .; Блатник, С .; Spegel, M .; Завсек, С. (декабрь 2001 г.). «Метод подвижных клеточных автоматов для моделирования материалов с мезоструктурой» (PDF). Теоретическая и прикладная механика разрушения. 37 (1–3): 311–334. Дои:10.1016 / S0167-8442 (01) 00079-9. Архивировано из оригинал (PDF) 19 июля 2011 г.
• Псахие, С.Г .; Смолин, А.Ю .; Стефанов, Ю.П .; Макаров, П.В .; Чертов, М.А. (2004). «Моделирование поведения сложных сред путем совместного использования дискретного и континуального подходов». Письма по технической физике. 30 (9): 712–714. Дои:10.1134/1.1804572.
• Shimizu, Y .; Hart, R .; Кундалл, П. (2004). Численное моделирование в микромеханике методами частиц. ISBN  978-90-5809-679-1. Получено 2010-03-03.
• Gnecco, E .; Мейер Э., ред. (2007). Основы трения и износа в наномасштабе. ISBN  978-3-540-36806-9. Получено 2010-03-03.
• Юньлян, Тан; Гуйронг, Тэн; Хайтао, Ли (2008). «Модель MCA для моделирования разрушения микронеоднородных материалов». Журнал наноматериалов. 2008: 1–7. Дои:10.1155/2008/946038. 946038.
• Фомин, В.М .; Андреев, А.Н .; и другие. (2008). Механика - от дискретной к непрерывной. Российская академия наук, Сибирское отделение, Институт теоретической и прикладной механики (им. С.А.Христиановича). п. 344. ISBN  978-5-7692-0974-1. (Фомин, В.М .; Андреев А.Н. и др. (2008). Механика - от дискретного к сплошному (на русском). Рос. акад наук, Сиб. отд-ние, Ин-т теоретической и прикладной механики им. С.А. Христиановича. п. 344. ISBN  978-5-7692-0974-1. Архивировано из оригинал 6 октября 2011 г.. Получено 3 марта 2010.)
• Смолин, А.Ю .; Роман, Н.В .; Добрынин, С.А .; Псахие, С.Г. (май – август 2009 г.). «О вращении в методе подвижного клеточного автомата». Физическая мезомеханика. 12 (3–4): 124–129. Дои:10.1016 / j.physme.2009.07.004.
• Попов, Валентин Л. (2009). Kontaktmechanik und Reibung (Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation). Springer Berlin Heidelberg. Дои:10.1007/978-3-540-88837-6. ISBN  978-3-540-88836-9.
• Добрынин, С.А. (2010). Разработка метода подвижного сотового атоматона для моделирования генерации и распространения упругих волн при контактном взаимодействии твердых тел.. Томск: кандидатская диссертация по физико-математическим наукам. п. 130. (Добрынин, С.А. (2010). Развитие метода подвижных клеточных автоматов для моделирования генерации и упругих волн при контактном взаимодействии твердого тел (на русском). Томск: Диссертация… кандидата физико-математических наук. п. 130. Получено 3 марта 2010.)
• Добрынин, Сергей (2011). Компьютерное моделирование методом подвижного клеточного автомата. Саарбрюккен, Германия: Академическое издательство LAP LAMBERT. п. 132. ISBN  978-3-8443-5954-1. (Добрынин, Сергей (2011). Компьютерное моделирование методом подвижных клеточных автоматов (на русском). Саарбрюккен, Германия: Академическое издательство LAP LAMBERT. п. 132. ISBN  978-3-8443-5954-1. Получено 2011-11-19.)

Программного обеспечения

• Программный пакет MCA
• Программа для моделирования материалов в дискретно-непрерывном подходе «FEM + MCA»: Номер государственной регистрации в Фонде прикладных исследований алгоритмов и программного обеспечения (AFAS): 50208802297 / Смолин А.Ю., Зелепугин С.А., Добрынин С.А.; заявителем и центром развития является Томский государственный университет. - дата регистрации 28.11.2008 г .; свидетельство AFAS N 11826 от 01.12.2008г.