Синусоидальная спираль - Sinusoidal spiral
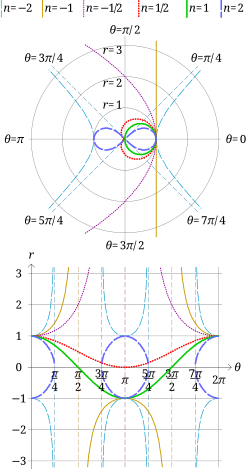
В геометрия, то синусоидальные спирали представляют собой семейство кривых, определяемых уравнением в полярные координаты
куда а - ненулевая постоянная и п - рациональное число, отличное от 0. При вращении вокруг начала координат это также можно записать
Термин «спираль» употребляется неправильно, потому что на самом деле они не спирали, и часто имеют форму цветка. Многие хорошо известные кривые представляют собой синусоидальные спирали, в том числе:
- Прямоугольная гипербола (п = −2)
- Линия (п = −1)
- Парабола (п = −1/2)
- Чирнхаузена кубическая (п = −1/3)
- Секстет Кэли (п = 1/3)
- Кардиоидный (п = 1/2)
- Круг (п = 1)
- Лемниската Бернулли (п = 2)
Кривые впервые были изучены Колин Маклорен.
Уравнения
Дифференцировать
и устранение а дает дифференциальное уравнение для р и θ:
- .
потом
откуда следует, что полярная тангенциальный угол является
и поэтому тангенциальный угол равен
- .
(Знак здесь положительный, если р и потому пθ имеют тот же знак и отрицательны в противном случае.)
Единичный касательный вектор,
- ,
имеет длину один, поэтому сравнение величины векторов с каждой стороны приведенного выше уравнения дает
- .
В частности, длина одной петли при является:
В кривизна дан кем-то
- .
Характеристики
В обратный синусоидальной спирали относительно окружности с центром в начале координат является другой синусоидальной спиралью, значение которой п отрицательное значение исходной кривой п. Например, обратная лемнискате Бернулли - прямоугольная гипербола.
В изоптический, педаль и отрицательная педаль синусоидальной спирали - это разные синусоидальные спирали.
Один путь частицы, движущейся согласно центральная сила пропорционально мощности р представляет собой синусоидальную спираль.
Когда п целое число, а п точки расположены равномерно по кругу радиуса а, то набор точек так, чтобы среднее геометрическое расстояние от точки до п точек представляет собой синусоидальную спираль. В этом случае синусоидальная спираль представляет собой полиномиальная лемниската.
Рекомендации
- Йетс, Р.К .: Справочник по кривым и их свойствам, Дж. У. Эдвардс (1952), "Спираль" стр. 213–214
- "Синусоидальная спираль" на www.2dcurves.com
- "Синусоидальные спирали" в The MacTutor History of Mathematics
- Вайсштейн, Эрик В. «Синусоидальная спираль». MathWorld.











