Поле уклона - Slope field

Поле наклона dy / dx = x²-x-2, с синей, красной и бирюзовой линиями (x³/ 3) - (х²/ 2) -2x + 4, (x³/ 3) - (х²/ 2) -2x и (x³/ 3) - (х²/ 2) -2х-4 соответственно.

Решения первого порядка дифференциальное уравнение^[1] скалярной функции y (x) можно нарисовать в 2-мерном пространстве с x по горизонтали и y по вертикали. Возможные решения - это функции y (x), нарисованные сплошными линиями. Иногда решение дифференциального уравнения бывает слишком громоздким аналитически. Тогда все еще можно нарисовать касательные кривых функций, например. на регулярной сетке. Касательные касаются функций в точках сетки. Однако поле направлений не зависит от хаотических аспектов дифференциального уравнения.

Определение

Стандартный корпус

Поле уклона может быть определено для следующего типа дифференциальных уравнений

${\displaystyle y'=f(x,y)}$,

что можно геометрически интерпретировать как склон из касательная к график решения дифференциального уравнения (интегральная кривая ) в каждой точке (Икс, у) как функция координат точки.^[2]

Его можно рассматривать как творческий способ построить вещественную функцию двух реальных переменных. ${\displaystyle f(x,y)}$ как плоское изображение. В частности, для данной пары ${\displaystyle x,y}$, вектор с компонентами ${\displaystyle [1,f(x,y)]}$ нарисован в точке ${\displaystyle x,y}$ на ${\displaystyle x,y}$-самолет. Иногда вектор ${\displaystyle [1,f(x,y)]}$ нормализовано, чтобы сделать сюжет более привлекательным для человеческого глаза. Набор пар ${\displaystyle x,y}$ создание прямоугольной сетки обычно используется для рисования.

An изоклина (серия линий с одинаковым уклоном) часто используется для дополнения поля уклона. В уравнении вида ${\displaystyle y'=f(x,y)}$, изоклина - это линия в ${\displaystyle x,y}$-самолет получен установкой ${\displaystyle f(x,y)}$ равно константе.

Общий случай системы дифференциальных уравнений

Учитывая систему дифференциальных уравнений,

${\displaystyle {\frac {dx_{1}}{dt}}=f_{1}(t,x_{1},x_{2},\ldots ,x_{n})}$

${\displaystyle {\frac {dx_{2}}{dt}}=f_{2}(t,x_{1},x_{2},\ldots ,x_{n})}$

${\displaystyle \vdots }$

${\displaystyle {\frac {dx_{n}}{dt}}=f_{n}(t,x_{1},x_{2},\ldots ,x_{n})}$

поле уклона представляет собой массив отметок уклона в фазовое пространство (в любом количестве измерений в зависимости от количества релевантных переменных; например, два в случае линейного ODE, как видно справа). Каждая отметка уклона центрируется в точке ${\displaystyle (t,x_{1},x_{2},\ldots ,x_{n})}$ и параллельна вектору

${\displaystyle {\begin{pmatrix}1\\f_{1}(t,x_{1},x_{2},\ldots ,x_{n})\\f_{2}(t,x_{1},x_{2},\ldots ,x_{n})\\\vdots \\f_{n}(t,x_{1},x_{2},\ldots ,x_{n})\end{pmatrix}}}$.

Количество, положение и длина отметок откоса могут быть произвольными. Позиции обычно выбираются так, чтобы точки ${\displaystyle (t,x_{1},x_{2},\ldots ,x_{n})}$ сделать равномерную сетку. Стандартный случай, описанный выше, представляет собой ${\displaystyle n=1}$. Общий случай поля наклонов для систем дифференциальных уравнений нелегко представить для ${\displaystyle n>2}$.

Общее приложение

С помощью компьютеров сложные поля наклона могут быть быстро созданы без утомления, поэтому лишь недавно они стали применяться на практике, чтобы просто почувствовать, каким должно быть решение, прежде чем искать явное общее решение. Конечно, компьютеры также могут решить эту проблему, если она существует.

Если нет явного общего решения, компьютеры могут использовать поля наклона (даже если они не показаны) для численного поиска графических решений. Примеры таких процедур: Метод Эйлера, а лучше Методы Рунге – Кутты.

Программное обеспечение для построения полей уклонов

Различные программные пакеты могут строить поля уклона.

Код поля направления в GNU Octave /MATLAB

веселье = @(Икс,у)у-Икс;                        % функция f (x, y) = y-x[Икс,у]=сетка(-5:0.5:5);                % интервалы для x и yсклоны=веселье(Икс,у);                        % матрица значений наклонаdy=склоны./sqrt(1+склоны.^2);            % нормализовать элемент строки ...dx=те(длина(dy))./sqrt(1+склоны.^2);  % ... величины для dy и dxчас=колчан(Икс,у,dx,dy,0.5);                 % построить поле направлениянабор (час, "maxheadsize", 0.1);             % изменить размер головы

Пример кода для Максима

/ * поле для y '= xy (щелкните точку, чтобы получить интегральную кривую) * / plotdf (x * y, [x, -2,2], [y, -2,2]);

Пример кода для Mathematica

(* поле для y '= xy *)VectorPlot[{1,Икс*у},{Икс,-2,2},{у,-2,2}]

Пример кода для SageMath^[3]

var ('x, y') plot_slope_field (x * y, (x, -2,2), (y, -2,2))

Примеры

• у '= х / у
• 

  Поле уклона

• 

  Интегральные кривые

• 

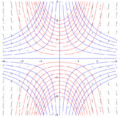
  Изоклины (синий), поле уклона (черный) и некоторые кривые решения (красный)

Смотрите также

• Примеры дифференциальных уравнений
• Векторное поле
• Преобразование Лапласа применяется к дифференциальным уравнениям
• Список тем о динамических системах и дифференциальных уравнениях
• Качественная теория дифференциальных уравнений

Рекомендации

1. Добрушкин Владимир Александрович (2014). Прикладные дифференциальные уравнения: начальный курс. CRC Press. п. 13. ISBN  978-1-4987-2835-5.
2. Андрей Д. Полянин; Александр Васильевич Манжиров (2006). Справочник по математике для инженеров и ученых. CRC Press. п. 453. ISBN  978-1-58488-502-3.
3. https://doc.sagemath.org/html/en/reference/plotting/sage/plot/plot_field.html

• Бланшар, Поль; Девани, Роберт Л.; и Холл, Глен Р. (2002). Дифференциальные уравнения (2-е изд.). Брукс / Коул: обучение Томпсона. ISBN  0-534-38514-1

внешняя ссылка

• Вайсштейн, Эрик В. «Склонное поле». MathWorld.
• Плоттер уклонного поля (Java)
• Плоттер поля уклона (JavaScript)