Сверхрешетка - Superlattice

А сверхрешетка представляет собой периодическую структуру слоев из двух (или более) материалов. Обычно толщина одного слоя составляет несколько нанометры. Он также может относиться к структуре более низкой размерности, такой как массив квантовые точки или же квантовые провода.

Открытие

Сверхрешетки были открыты в начале 1925 года Йоханссоном и Линде.^[1] после учебы на золото -медь и палладий -медные системы через их специальные дифрактограммы. Дальнейшие экспериментальные наблюдения и теоретические модификации поля были выполнены Брэдли и Джеем,^[2] Горский,^[3] Борелиус,^[4] Делингер и Граф,^[5] Брэгг и Уильямс^[6] и Бете.^[7] Теории основывались на переходе расположения атомов в кристаллических решетках из беспорядочный заявить упорядоченный государственный.

Механические свойства

J.S. Келер теоретически предсказал^[8] что за счет использования чередующихся (нано) слоев материалов с высокими и низкими упругими постоянными сопротивление сдвигу повышается до 100 раз по сравнению с Фрэнк – Прочитать источник из вывихи не может работать в нанослоях.

Повышенная механическая твердость такие материалы сверхрешетки были впервые подтверждены Lehoczky в 1978 году на Al-Cu и Al-Ag,^[9] и позже несколькими другими, например Барнетт и Спроул^[10] на жестком PVD покрытия.

Свойства полупроводника

Если сверхрешетка состоит из двух полупроводниковых материалов с разными запрещенные зоны, каждый квантовая яма устанавливает новые правила отбора которые влияют на условия прохождения зарядов через конструкцию. Два разных полупроводниковых материала попеременно наносятся друг на друга, образуя периодическую структуру в направлении роста. С 1970 г. предложение синтетических сверхрешеток Esaki и Цу,^[11] Были достигнуты успехи в физике таких ультратонких полупроводников, которые в настоящее время называются квантовыми структурами. Концепция чего-либо квантовое ограничение привело к наблюдению квантовых размерных эффектов в изолированных гетероструктурах с квантовыми ямами и тесно связано со сверхрешетками через явления туннелирования. Поэтому эти две идеи часто обсуждаются на одной и той же физической основе, но каждая имеет разную физику, полезную для приложений в электрических и оптических устройствах.

Типы полупроводниковых сверхрешеток

Структура минизоны сверхрешетки зависит от гетероструктура типа, либо тип I, тип II или же тип III. Для типа I нижняя часть зона проводимости и верх валентной подзоны сформирован в одном и том же полупроводниковом слое. В типе II подзоны проводимости и валентности разнесены как в реальном, так и в взаимное пространство, так что электроны и дырки удерживаются в разных слоях. Сверхрешетки типа III включают полуметалл материал, такой как HgTe /CdTe. Хотя нижняя часть подзоны проводимости и верх валентной подзоны сформированы в одном и том же полупроводниковом слое в сверхрешетке типа III, которая аналогична сверхрешетке типа I, запрещенная зона сверхрешетки типа III может плавно регулироваться от полупроводниковой до нулевой зоны. материал зазора и полуметалл с отрицательной шириной запрещенной зоны.

Другой класс квазипериодических сверхрешеток назван в честь Фибоначчи. Сверхрешетку Фибоначчи можно рассматривать как одномерную квазикристалл, где прыжковая передача электронов или локальная энергия принимают два значения, расположенных в Последовательность Фибоначчи.

Полупроводниковые материалы

Сверхрешетка GaAs / AlAs и потенциальный профиль зоны проводимости и валентной зоны вдоль направления роста (z).

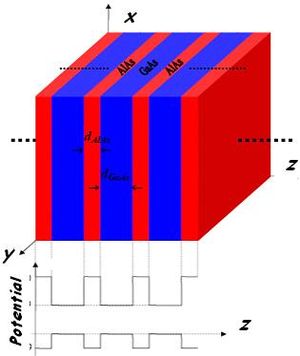
Полупроводниковые материалы, которые используются для изготовления структур сверхрешеток, можно разделить на группы элементов, IV, III-V и II-VI. В то время как полупроводники III-V групп (особенно GaAs / Al_ИксGa_1-хAs), гетероструктуры IV группы, такие как Si_ИксGe_1-х системы намного сложнее реализовать из-за большого рассогласования решеток. Тем не менее деформационная модификация подзонных структур в этих квантовых структурах представляет интерес и привлекает большое внимание.

В системе GaAs / AlAs как разница в постоянной решетки между GaAs и AlAs, так и разница в их коэффициенте теплового расширения невелики. Таким образом, остаточная деформация при комнатной температуре может быть минимизирована после охлаждения от эпитаксиальный рост температуры. Первая композиционная сверхрешетка была реализована с использованием GaAs / Al_ИксGa_1-хКак материальная система.

А графен /нитрид бора Система образует полупроводниковую сверхрешетку после совмещения двух кристаллов. Его носители заряда движутся перпендикулярно электрическому полю с небольшой диссипацией энергии. h-BN имеет шестиугольник структура похожа на графен. Сверхрешетка сломалась инверсионная симметрия. Локально топологические токи сопоставимы по силе с приложенным током, что указывает на большие углы долины-Холла.^[12]

Производство

Сверхрешетки можно изготавливать различными способами, но наиболее распространенными являются: молекулярно-лучевая эпитаксия (MBE) и распыление. С помощью этих методов можно изготавливать слои толщиной всего в несколько атомных расстояний. Примером задания сверхрешетки является [Fe
₂₀V
₃₀]₂₀. Он описывает двойной слой из 20 Å железа (Fe) и 30 Å ванадия (V), повторенный 20 раз, что дает общую толщину 1000 Å или 100 нм. Технология МЛЭ как способ изготовления полупроводниковых сверхрешеток имеет первостепенное значение. Помимо технологии MBE, металлоорганическое химическое осаждение из паровой фазы (MO-CVD) внесла свой вклад в развитие сверхпроводниковых сверхрешеток, которые состоят из полупроводников на основе четверных соединений III-V, таких как сплавы InGaAsP. Новые методы включают комбинацию обращения с источником газа с технологиями сверхвысокого вакуума (UHV), такими как металлоорганические молекулы в качестве исходных материалов и MBE источника газа с использованием гибридных газов, таких как арсин (Пепел
₃) и фосфин (PH
₃) были разработаны.

Вообще говоря, МБЭ - это метод использования трех температур в бинарных системах, например, температуры подложки, температуры исходного материала элементов III группы и элементов V группы в случае соединений III-V.

Структурное качество полученных сверхрешеток можно проверить с помощью дифракция рентгеновских лучей или же нейтронография спектры, содержащие характерные сателлитные пики. Другие эффекты, связанные с чередованием слоев: гигантское магнитосопротивление, настраиваемая отражательная способность для рентгеновских и нейтронных зеркал, нейтронные спиновая поляризация, а также изменения упругих и акустических свойств. В зависимости от природы составляющих сверхрешетку можно назвать магнитный, оптический или же полупроводник.

Рентгеновское и нейтронное рассеяние на [Fe₂₀V₃₀]₂₀ сверхрешетка.

Структура минизоны

Схематическая структура периодической сверхрешетки показана ниже, где A и B - два полупроводниковых материала с соответствующей толщиной слоя. а и б (период: ${\displaystyle d=a+b}$). Когда а и б не слишком малы по сравнению с межатомным расстоянием, адекватное приближение получается заменой этих быстро меняющихся потенциалов эффективным потенциалом, полученным из зонной структуры исходных объемных полупроводников. Несложно решить одномерные уравнения Шредингера в каждом из отдельных слоев, решения которых ${\displaystyle \psi }$ являются линейными комбинациями действительных или мнимых экспонент.

При большой толщине барьера туннелирование является слабым возмущением по отношению к несвязанным бездисперсионным состояниям, которые также полностью ограничены. В этом случае дисперсионное соотношение ${\displaystyle E_{z}(k_{z})}$, периодическая более ${\displaystyle 2\pi /d}$ с более ${\displaystyle d=a+b}$ в силу теоремы Блоха полностью синусоидален:

${\displaystyle \ E_{z}(k_{z})={\frac {\Delta }{2}}(1-\cos(k_{z}d))}$

а эффективная масса меняет знак при ${\displaystyle 2\pi /d}$:

${\displaystyle \ {m^{*}={\frac {\hbar ^{2}}{\partial ^{2}E/\partial k^{2}}}}|_{k=0}}$

В случае мини-зон этот синусоидальный характер больше не сохраняется. Только высоко в мини-зоне (для волновых векторов далеко за пределами ${\displaystyle 2\pi /d}$) является фактически «обнаруженным» верхом и меняет знак эффективной массы. Форма дисперсии минизоны оказывает сильное влияние на транспорт минизоны, поэтому для больших минизон требуются точные расчеты дисперсионного соотношения. Условием наблюдения за переносом одной минизоны является отсутствие передачи между минизонами каким-либо процессом. Тепловой квант k_BТ должно быть намного меньше разницы энергий ${\displaystyle E_{2}-E_{1}}$ между первой и второй мини-зоной, даже при наличии приложенного электрического поля.

Блох заявляет

Для идеальной сверхрешетки полный набор собственные состояния состояния могут быть построены из произведений плоских волн ${\displaystyle e^{i\mathbf {k} \cdot \mathbf {r} }/2\pi }$ и z-зависимая функция ${\displaystyle f_{k}(z)}$ которое удовлетворяет уравнению на собственные значения

${\displaystyle \left(E_{c}(z)-{\frac {\partial }{\partial z}}{\frac {\hbar ^{2}}{2m_{c}(z)}}{\frac {\partial }{\partial z}}+{\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{c}(z)}}\right)f_{k}(z)=Ef_{k}(z)}$.

В качестве ${\displaystyle E_{c}(z)}$ и ${\displaystyle m_{c}(z)}$ - периодические функции с периодом сверхрешетки d, собственные состояния Состояние Блоха ${\displaystyle f_{k}(z)=\phi _{q,\mathbf {k} }(z)}$ с энергией ${\displaystyle E^{\nu }(q,\mathbf {k} )}$. В рамках первого порядка теория возмущений в k², получаем энергию

${\displaystyle E^{\nu }(q,\mathbf {k} )\approx E^{\nu }(q,\mathbf {0} )+\langle \phi _{q,\mathbf {k} }\mid {\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{c}(z)}}\mid \phi _{q,\mathbf {k} }\rangle }$.

Сейчас же, ${\displaystyle \phi _{q,\mathbf {0} }(z)}$ будет иметь большую вероятность в скважине, поэтому кажется разумным заменить второй член на

${\displaystyle E_{k}={\frac {\hbar ^{2}\mathbf {k} ^{2}}{2m_{w}}}}$

куда ${\displaystyle m_{w}}$ - эффективная масса квантовой ямы.

Функции Ванье

По определению Блоховские функции делокализованы по всей сверхрешетке. Это может вызвать трудности при приложении электрических полей или при учете эффектов, связанных с конечной длиной сверхрешетки. Поэтому часто бывает полезно использовать разные наборы базовых состояний, которые лучше локализованы. Заманчивым выбором было бы использование собственных состояний одиночных квантовых ям. Тем не менее, у такого выбора есть серьезный недостаток: соответствующие состояния являются решениями двух разных Гамильтонианы, каждый хорошо пренебрегая присутствием другого. Таким образом, эти состояния не ортогональны, что создает сложности. Обычно в рамках этого подхода связь оценивается с помощью гамильтониана переноса. По этим причинам удобнее использовать набор Функции Ванье.

Лестница Ванье – Старка

Приложение электрического поля F к структуре сверхрешетки заставляет гамильтониан проявлять дополнительный скалярный потенциал eφ(z) = −eFz что нарушает трансляционную инвариантность. В этом случае, учитывая собственное состояние с волновой функцией ${\displaystyle \Phi _{0}(z)}$ и энергия ${\displaystyle E_{0}}$, то множество состояний, соответствующих волновым функциям ${\displaystyle \Phi _{j}(z)=\Phi _{0}(z-jd)}$ являются собственными состояниями гамильтониана с энергиями E_j = E₀ − jeFd. Эти состояния равномерно распределены как по энергии, так и в реальном пространстве и образуют так называемые Лестница Ванье – Старка. Потенциал ${\displaystyle \Phi _{0}(z)}$ не ограничен для бесконечного кристалла, что подразумевает непрерывный энергетический спектр. Тем не менее характерный энергетический спектр этих лестниц Ванье – Штарка удалось разрешить экспериментально.

Транспорт

Обзор различных стандартных подходов к сверхрешеточному транспорту.

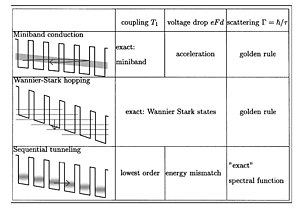
Движение носителей заряда в сверхрешетке отличается от движения в отдельных слоях: мобильность носителей заряда могут быть улучшены, что выгодно для высокочастотных устройств, а особые оптические свойства используются в полупроводниковые лазеры.

Если к проводнику, такому как металл или полупроводник, приложено внешнее смещение, обычно генерируется электрический ток. Величина этого тока определяется зонной структурой материала, процессами рассеяния, напряженностью приложенного поля и равновесным распределением носителей заряда в проводнике.

Частный случай сверхрешеток, названный супер полосы сделаны из сверхпроводящих элементов, разделенных прокладками. В каждой минизоне сверхпроводящий параметр порядка, называемый сверхпроводящей щелью, принимает разные значения, создавая многощелевую, двухщелевую или многозонную сверхпроводимость.

Недавно Феликс и Перейра исследовали перенос тепла фононами в периодических^[13] и квазипериодический^[14][15] сверхрешетки графен-hBN по последовательности Фибоначчи. Они сообщили, что вклад когерентного переноса тепла (фононы, подобные волне) подавлялся по мере увеличения квазипериодичности.

Другие размеры

Вскоре двумерные электронные газы (2DEG ) стали общедоступными для экспериментов, исследовательские группы пытались создать структуры^[16] это можно было бы назвать 2D искусственными кристаллами. Идея состоит в том, чтобы подчинить электроны интерфейс между двумя полупроводниками (т.е. вдоль z-направление) к дополнительному модулирующему потенциалу V(Икс,у). В отличие от классических сверхрешеток (1D / 3D, то есть одномерной модуляции электронов в трехмерном объеме), описанных выше, это обычно достигается обработкой поверхности гетероструктуры: нанесением металлического затвора с соответствующим рисунком или травлением. Если амплитуда V(Икс,у) большой (взять ${\displaystyle V(x,y)=-V_{0}(\cos 2\pi x/a+\cos 2\pi y/a),V_{0}>0}$ в качестве примера) по сравнению с уровнем Ферми, ${\displaystyle |V_{0}|\gg E_{f}}$, электроны в сверхрешетке должны вести себя аналогично электронам в атомном кристалле с квадратной решеткой (в примере эти «атомы» будут расположены в положениях (на,ма) куда п,м целые числа).

Разница в длине и шкале энергии. Постоянные решетки атомных кристаллов имеют порядок 1 Å, а сверхрешетки (а) на несколько сотен или тысяч больше, что диктуется технологическими ограничениями (например, электронно-лучевая литография, используемая для формирования рисунка на поверхности гетероструктуры). Соответственно меньше энергии в сверхрешетках. Используя простую квантово-механическую ограниченная частица модель предлагает ${\displaystyle E\propto 1/a^{2}}$. Это соотношение является лишь приблизительным ориентиром и фактическими расчетами с актуальными в настоящее время графен (природный атомный кристалл) и искусственный графен^[17] (сверхрешетка) показывают, что характерные ширины зон составляют порядка 1 эВ и 10 мэВ соответственно. В режиме слабой модуляции (${\displaystyle |V_{0}|\ll E_{f}}$), такие явления, как колебания соизмеримости или фрактальные энергетические спектры (Бабочка Хофштадтера ) происходить.

Искусственные двухмерные кристаллы можно рассматривать как случай 2D / 2D (2D-модуляция 2D-системы), и экспериментально доступны другие комбинации: массив квантовых проводов (1D / 2D) или 3D / 3D. фотонные кристаллы.

Приложения

Сверхрешетка системы палладий-медь используется в сплавах с высокими эксплуатационными характеристиками, чтобы обеспечить более высокую электропроводность, чему способствует упорядоченная структура. Другие легирующие элементы, такие как серебро, рений, родий и рутений добавлены для повышения механической прочности и устойчивости к высоким температурам. Этот сплав используется для игл зондов в карты датчиков.^[18]

Смотрите также

• Функция Ванье
• Трубчатые наноструктуры

Рекомендации

1. Йоханссон; Линде (1925). «Рентгенологическое определение расположения атомов в смешанных кристаллах серии золото-медь и палладий-медь». Annalen der Physik. 78 (21): 439. Bibcode:1925АнП ... 383..439J. Дои:10.1002 / andp.19253832104.
2. Брэдли; Джей (1932). «Образование сверхрешеток в сплавах железа и алюминия». Proc. R. Soc. А. 136 (829): 210–232. Bibcode:1932RSPSA.136..210B. Дои:10.1098 / RSPA.1932.0075.
3. Горского (1928). «Рентгеновские исследования превращений в сплаве CuAu». Z. Phys. 50 (1–2): 64–81. Bibcode:1928ZPhy ... 50 ... 64G. Дои:10.1007 / BF01328593.
4. Борелиус (1934). «Теория превращений металлических смешанных фаз». Annalen der Physik. 20 (1): 57. Bibcode:1934АнП ... 412 ... 57Б. Дои:10.1002 / andp.19344120105.
5. Делингер; Граф (1934). «Превращение твердых металлических фаз I. Тетрагональный сплав золота с медью CuAu». Z. Phys. Chem. 26: 343.
6. Bragg, W.L .; Уильямс, Э.Дж. (1934). «Влияние теплового перемешивания на расположение атомов в сплавах I». Proc. R. Soc. А. 145 (855): 699–730. Bibcode:1934RSPSA.145..699B. Дои:10.1098 / rspa.1934.0132.
7. Бете (1935). «Статистическая теория сверхрешеток». Proc. R. Soc. А. 150 (871): 552–575. Bibcode:1935RSPSA.150..552B. Дои:10.1098 / rspa.1935.0122.
8. Кёлер, Дж. (1970). «Попытка создать прочное твердое тело». Физический обзор B. 2 (2): 547–551. Bibcode:1970ПхРвБ ... 2..547К. Дои:10.1103 / PhysRevB.2.547.
9. Лехоцкий, С. Л. (1973). «Замедление образования и движения дислокаций в тонкослойных металлических ламинатах». Acta Metallurgica. 41 (26): 1814.
10. Яшар, П .; Barnett, S.A .; Rechner, J .; Спроул, В. Д. (1998). «Структура и механические свойства поликристаллических сверхрешеток CrN / TiN». Журнал вакуумной науки и технологий A: вакуум, поверхности и пленки. Американское вакуумное общество. 16 (5): 2913–2918. Дои:10.1116/1.581439. ISSN  0734-2101.
11. Esaki, L .; Цу Р. (1970). «Сверхрешетка и отрицательная дифференциальная проводимость в полупроводниках». Журнал исследований и разработок IBM. 14: 61–65. Дои:10.1147 / ряд.141.0061.
12. Горбачев, Р. В .; Song, J. C. W .; Ю., Г. Л .; Кретинин, А. В .; Холка, F .; Cao, Y .; Мищенко, А .; Григорьева, И. В .; Новоселов, К. С .; Левитов, Л. С .; Гейм, А. К. (2014). «Обнаружение топологических токов в сверхрешетках графена». Наука. 346 (6208): 448–451. arXiv:1409.0113. Bibcode:2014Наука ... 346..448G. Дои:10.1126 / science.1254966. PMID  25342798.
13. Феликс, Исаак М .; Перейра, Луис Фелипе С. (9 февраля 2018 г.). «Теплопроводность лент сверхрешетки графен-hBN». Научные отчеты. 8 (1): 2737. Дои:10.1038 / s41598-018-20997-8. ЧВК  5807325. PMID  29426893.
14. Феликс, Исаак М .; Перейра, Луис Фелипе С. (30 апреля 2020 г.). «Подавление когерентного переноса тепла в квазипериодических лентах сверхрешетки графен-hBN». Углерод. 160: 335–341. arXiv:2001.03072. Дои:10.1016 / j.carbon.2019.12.090.
15. Феликс, Исаак де Македу (4 августа 2020 г.). "Condução de calor em nanofitas quase-periódicas de grafeno-hBN" (на португальском).
16. Heitmann, D .; Коттхаус, Дж. Р. П. (1993). "Спектроскопия массивов квантовых точек". Физика сегодня. 46 (6): 56. Bibcode:1993ФТ .... 46ф..56Х. Дои:10.1063/1.881355.
17. Kato, Y .; Endo, A .; Katsumoto, S .; Ай, Ю. (2012). «Геометрические резонансы в магнитосопротивлении гексагональных боковых сверхрешеток». Физический обзор B. 86 (23): 235315. arXiv:1208.4480. Bibcode:2012PhRvB..86w5315K. Дои:10.1103 / PhysRevB.86.235315.
18. «Патент США US10385424B2 Сплавы на основе палладия» (PDF). патенты google. Получено 19 июн 2020.

• H.T. Гран, «Полупроводниковые сверхрешетки», World Scientific (1995). ISBN  978-981-02-2061-7
• Шуллер, И. (1980). «Новый класс слоистых материалов». Письма с физическими проверками. 44 (24): 1597–1600. Bibcode:1980ПхРвЛ..44.1597С. Дои:10.1103 / PhysRevLett.44.1597.
• Мортен Ягд Кристенсен, «Эпитаксия, тонкие пленки и сверхрешетки», Национальная лаборатория Рисё, (1997). ISBN  8755022987 Сверхрешетка в Google Книги [1]
• К. Хамагучи, «Основы физики полупроводников», Спрингер (2001). Сверхрешетка в Google Книги ISBN  3540416390
• Вакер, А. (2002). «Полупроводниковые сверхрешетки: модельная система для нелинейного транспорта». Отчеты по физике. 357 (1): 1–7. arXiv:cond-mat / 0107207. Bibcode:2002PhR ... 357 .... 1Вт. CiteSeerX  10.1.1.305.3634. Дои:10.1016 / S0370-1573 (01) 00029-1.
• Haugan, H.J .; Szmulowicz, F .; Махалингам, К .; Brown, G.J .; Munshi, S. R .; Ульрих, Б. (2005). «Короткопериодические сверхрешетки InAs ∕ GaSb типа II для детекторов среднего инфракрасного диапазона». Письма по прикладной физике. 87 (26): 261106. Bibcode:2005ApPhL..87z1106H. Дои:10.1063/1.2150269. [2]^{[мертвая ссылка ]}

дальнейшее чтение

• Mendez, E.E .; Ублюдок, Г. (1993). «Лестницы Ванье-Штарка и блоховские колебания в сверхрешетках». Физика сегодня. 46 (6): 34–42. Bibcode:1993ФТ .... 46ф..34М. Дои:10.1063/1.881353.