Квантовая яма - Quantum well

А квантовая яма это потенциальная яма только с дискретными значениями энергии.
Классическая модель, используемая для демонстрации квантовой ямы, заключается в ограничении частиц, которые изначально могли свободно перемещаться в трех измерениях, в двух измерениях, заставляя их занимать плоскую область. Эффекты квантовое ограничение происходят, когда толщина квантовой ямы становится сравнимой с длина волны де Бройля перевозчиков (обычно электроны и дыры ), что приводит к уровням энергии, называемым «подзонами энергии», т.е. носители могут иметь только дискретные значения энергии.
На основе теории систем с квантовыми ямами было разработано множество электронных устройств с квантовыми ямами. Эти устройства нашли применение в лазеры, фотоприемники, модуляторы и переключатели Например. По сравнению с обычными устройствами, устройства с квантовыми ямами намного быстрее, работают намного экономичнее и имеют невероятное значение для технологической и телекоммуникационной отраслей. Эти устройства с квантовыми ямами в настоящее время заменяют многие, если не все, обычные электрические компоненты во многих электронных устройствах.[2]
Концепция квантовой ямы была независимо предложена в 1963 г. Герберт Кремер и по Жорес Алферов и Р.Ф. Казаринов.[3][4]
История
В полупроводник квантовая яма была разработана в 1970 г. Esaki и Цу, который также изобрел синтетические сверхрешетки.[5] Они предложили гетероструктура состоящий из чередующихся тонких слоев полупроводников с различной шириной запрещенной зоны, должен проявлять интересные и полезные свойства.[6] С тех пор много усилий и исследований было направлено на изучение физики систем с квантовыми ямами, а также на разработку устройств с квантовыми ямами.
Развитие устройств с квантовыми ямами во многом связано с достижениями в рост кристаллов техники. Это связано с тем, что для устройств с квантовыми ямами требуются структуры высокой чистоты с небольшим количеством дефектов. Следовательно, большой контроль над ростом этих гетероструктур позволяет разрабатывать полупроводниковые устройства, которые могут иметь очень точно настраиваемые свойства.[5]
Квантовые ямы и физика полупроводников были горячей темой в физических исследованиях. Разработка полупроводниковых устройств с использованием структур, состоящих из нескольких полупроводников, принесла Нобелевские премии за Жорес Алферов и Герберт Кремер в 2000 г.[7]
Теория устройств с квантовыми ямами привела к значительному прогрессу в производстве и эффективности многих современных компонентов, таких как светодиоды, транзисторы Например. Сегодня такие устройства повсеместно используются в современных сотовых телефонах, компьютерах и многих других вычислительных устройствах.
Изготовление
Квантовые ямы образуются в полупроводниках из материала, например арсенид галлия, зажатый между двумя слоями материала с более широким запрещенная зона, любить арсенид алюминия. (Другие примеры: слой нитрид индия-галлия зажатый между двумя слоями нитрид галлия.) Эти структуры могут быть выращены молекулярно-лучевая эпитаксия или химическое осаждение из паровой фазы с контролем толщины слоя до монослои.
Тонкие металлические пленки также могут поддерживать состояния с квантовыми ямами, в частности, тонкие металлические покрывающие слои, выращенные на поверхностях металлов и полупроводников. Граница раздела вакуум-металл ограничивает электрон (или дырку) с одной стороны и, как правило, абсолютным зазором с полупроводниковыми подложками или выступающей запрещенной зоной с металлическими подложками.
Существует 3 основных подхода к выращиванию системы материалов с квантовой ямой: согласованная по решетке, сбалансированная по деформации и деформированная.[8]
- Система с согласованной решеткой: в системе с согласованной решеткой лунка и барьер имеют такую же постоянную решетки, что и основной материал подложки.[8] При использовании этого метода разница в ширине запрещенной зоны минимальна, дислокации, но также и минимальный сдвиг в спектре поглощения.
- Система со сбалансированной деформацией: в системе со сбалансированной деформацией углубление и барьер выращиваются таким образом, что увеличение постоянной решетки одного из слоев компенсируется уменьшением постоянной решетки в следующем по сравнению с материалом подложки. Выбор толщины и состава слоев влияет на требования к ширине запрещенной зоны и ограничения транспорта носителей. Такой подход обеспечивает максимальную гибкость конструкции, предлагая большое количество периодических квантовых ям с минимальной релаксацией деформации.[8]
- Деформированная система: деформированная система выращивается с колодцами и барьерами, которые не имеют одинаковой постоянной решетки. Напряженная система сжимает всю конструкцию. В результате структура может вместить только несколько квантовых ям.[8]

Описание и обзор
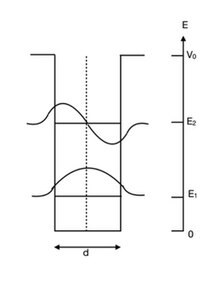
Одну из простейших систем с квантовыми ямами можно построить, вставив тонкий слой полупроводникового материала одного типа между двумя слоями другого с другой шириной запрещенной зоны. Рассмотрим для примера два слоя AlGaAs с большой шириной запрещенной зоны, окружающей тонкий слой GaAs с меньшей шириной запрещенной зоны. Предположим, изменение материала происходит вдоль z-направлении и, следовательно, потенциальная яма находится вдоль z-направление (без ограничения в x – y самолет.). Поскольку запрещенная зона содержащегося материала меньше, чем окружающего AlGaAs, квантовая яма (потенциальная яма) создается в области GaAs. Это изменение зонной энергии в структуре можно рассматривать как изменение потенциала, который будет ощущать носитель, поэтому носители низкой энергии могут быть захвачены в этих ямах. [7]

Внутри квантовой ямы имеются дискретные собственные состояния энергии что у перевозчиков может быть. Например, электрон в зона проводимости может иметь меньшую энергию внутри ямы, чем она могла бы иметь в области AlGaAs этой структуры. Следовательно, электрон в зоне проводимости с низкой энергией может быть захвачен внутри квантовой ямы. Точно так же дыры в валентной зоне могут быть захвачены в верхней части потенциальных ям, созданных в валентной зоне. Состояния, в которых могут находиться ограниченные носители: частицы в коробке -подобные состояния.[5]
Физика
Квантовые ямы и устройства с квантовыми ямами - это область физика твердого тела это все еще широко изучается и исследуется сегодня. Теория, используемая для описания таких систем, использует важные результаты из области квантовая физика, статистическая физика, и электродинамика.
Модель бесконечного колодца
Простейшей моделью системы квантовой ямы является модель бесконечной ямы. В этой модели предполагается, что стенки / барьеры потенциальной ямы бесконечны. Это приближение довольно нереалистично, так как потенциальные ямы, создаваемые в квантовых ямах, обычно имеют порядок нескольких сотен миллиметров.электронвольт, что намного меньше предполагаемого бесконечно высокого потенциала. Однако в первом приближении модель бесконечной ямы служит простой и полезной моделью, которая дает некоторое представление о физике квантовых ям.[5]
Рассмотрим бесконечную квантовую яму, ориентированную в z-направление, такое, что носители в скважине ограничены z-направление, но свободное движение в x – y самолет. мы выбираем квантовую яму, чтобы убежать от к . Мы предполагаем, что носители не испытывают потенциала внутри ямы и что потенциал в области барьера бесконечно велик.
В Уравнение Шредингера для носителей в модели бесконечной скважины составляет:
где является Постоянная Планка деленное на и это эффективная масса носителей в районе колодца. Эффективная масса носителя - это масса, которую электрон «ощущает» в своей квантовой среде, и она обычно различается для разных полупроводников, так как значение эффективной массы сильно зависит от кривизны зоны. Обратите внимание, что может быть эффективной массой электронов в яме в зоне проводимости или для дырок в яме в валентной зоне.
Решения и уровни энергии

Решение волновые функции не может существовать в барьерной области ямы из-за бесконечно высокого потенциала. Таким образом, при наложении следующих граничных условий получаются разрешенные волновые функции:
- .
Волновые функции решения имеют следующий вид:
- .
Нижний индекс , () обозначает целое число квантовое число и это волновой вектор связанные с каждым состоянием, указанным выше. Соответствующие дискретные энергии определяются как:
- .
Простая модель с бесконечной ямой обеспечивает хорошую отправную точку для анализа физики систем с квантовыми ямами и эффектов квантового ограничения. Модель правильно предсказывает, что энергии в колодце обратно пропорциональны квадрату длины колодца. Это означает, что точный контроль ширины полупроводниковых слоев, то есть длины ямы, позволит точно контролировать уровни энергии, разрешенные для носителей в ямах. Это невероятно полезное свойство для технология запрещенной зоны. Кроме того, модель показывает, что уровни энергии пропорциональны обратной величине эффективной массы. Следовательно, тяжелые и легкие дырки будут иметь разные энергетические состояния, когда они захвачены в яме. Тяжелые и легкие дыры возникают при совпадении максимумов валентных зон разной кривизны; что дает две разные эффективные массы.[5]
Недостатком модели бесконечной ямы является то, что она предсказывает гораздо больше энергетических состояний, чем существует, поскольку стенки реальных квантовых ям конечны. Модель также не учитывает тот факт, что в действительности волновые функции не стремятся к нулю на границе ямы, а «стекают» в стенку (из-за квантового туннелирования) и экспоненциально затухают до нуля. Это свойство позволяет проектировать и производить сверхрешетки и другие новые устройства с квантовыми ямами и лучше описывается моделью конечных ям.
Конечно-хорошо модель
Модель конечных ям обеспечивает более реалистичную модель квантовых ям. Здесь стенки ямы в гетероструктуре моделируются с использованием конечного потенциала , которая представляет собой разницу в энергиях зон проводимости различных полупроводников. Поскольку стенки конечны и электроны могут туннель в область барьера. Следовательно, разрешенные волновые функции будут проникать через барьерную стенку.[6]
Рассмотрим конечную квантовую яму, ориентированную в z-направление, такое, что носители в скважине ограничены z-направление, но свободное движение в x – y самолет. Мы выбираем квантовую яму, от которой бежим к . Мы предполагаем, что носители не имеют потенциала в пределах ямы и потенциала в барьерных областях.
Уравнение Шредингера для носителей внутри скважины не изменилось по сравнению с моделью бесконечной скважины, за исключением граничных условий на стенках, которые теперь требуют, чтобы волновые функции и их наклоны были непрерывными на границах.
В пределах барьерной области уравнение Шредингера для носителей гласит:
куда - эффективная масса носителя в области барьера, которая обычно отличается от его эффективной массы внутри ямы.[5]
Решения и уровни энергии
Используя соответствующие граничные условия и условие непрерывности волновой функции на краю скважины, получаем решения для волнового вектора которые удовлетворяют следующим трансцендентные уравнения:
и
- ,
где - экспоненциальная постоянная затухания в области барьера, которая является мерой того, насколько быстро волновая функция спадает до нуля в области барьера. Собственные состояния квантованной энергии внутри ямы, которые зависят от волнового вектора и квантового числа () даются:
- .
Постоянная экспоненциального затухания дан кем-то:
Это зависит от собственного состояния связанного носителя. , глубина колодца , а эффективная масса носителя в области барьера .
Решения трансцендентных уравнений выше можно легко найти, используя числовой или графические методы. Обычно существует всего несколько решений. Однако всегда найдется хотя бы одно решение, поэтому одно связанное состояние в скважине, независимо от того, насколько мал потенциал. Подобно бесконечной яме, волновые функции в яме синусоидальны, но экспоненциально затухают в барьере ямы. Это имеет эффект уменьшения связанных энергетических состояний квантовой ямы по сравнению с бесконечной ямой.[5]
Сверхрешетки

Сверхрешетка - это периодическая гетероструктура, состоящая из чередующихся материалов с различной шириной запрещенной зоны. Толщина этих периодических слоев обычно составляет порядка нескольких нанометров. Зонная структура, возникающая в результате такой конфигурации, представляет собой периодический ряд квантовых ям. Важно, чтобы эти барьеры были достаточно тонкими, чтобы носители могли туннелировать через барьерные области множества ям.[2] Определяющим свойством сверхрешеток является то, что барьеры между ямами достаточно тонкие для соединения соседних ям. Периодические структуры, состоящие из повторяющихся квантовых ям, которые имеют барьеры, слишком толстые для взаимодействия соседних волновых функций, называются структурами с множественными квантовыми ямами (МКЯ).[5]
Поскольку носители могут туннелировать через области барьера между ямами, волновые функции соседних ям соединяются через тонкий барьер, поэтому электронные состояния в сверхрешетках образуют делокализованные минизоны.[5] Решение для разрешенных энергетических состояний в сверхрешетках аналогично решению для конечных квантовых ям с изменением граничных условий, возникающих из-за периодичности структур. Поскольку потенциал периодический, математически систему можно описать аналогично одномерной кристаллической решетке.
Приложения
Из-за своей квазидвумерной природы электроны в квантовых ямах имеют плотность состояний как функция энергии, имеющая различные ступени, в отличие от плавной зависимости квадратного корня, которая встречается в объемных материалах. Кроме того, эффективная масса дырок в валентной зоне изменяется, чтобы более точно соответствовать массе электронов в валентной зоне. Эти два фактора вместе с уменьшенным количеством активного материала в квантовых ямах приводят к лучшим характеристикам оптических устройств, таких как лазерные диоды. В результате квантовые ямы широко используются в диодные лазеры, включая красные лазеры для DVD-дисков и лазерные указки, инфракрасные лазеры в оптоволоконных передатчиках или в синие лазеры. Их также используют для изготовления HEMTs (транзисторы с высокой подвижностью электронов), которые используются в малошумящей электронике. Квантовые инфракрасные фотоприемники также основаны на квантовых ямах и используются для инфракрасное изображение.
Легируя либо саму яму, либо предпочтительно барьер квантовой ямы донор примеси, а двумерный электронный газ (2DEG) может быть сформирован. Такая структура создает проводящий канал HEMT и имеет интересные свойства при низкой температуре. Одной из таких функций является квантовый эффект холла, видно на высоком магнитные поля. Акцептор легирующие примеси могут также приводить к образованию двумерного дырочного газа (2DHG).
Насыщающийся поглотитель
Квантовая яма может быть изготовлена как насыщающийся поглотитель, используя ее насыщающееся поглощение свойство. Насыщаемые поглотители широко используются в пассивных синхронизация режима лазеры. Полупроводниковые насыщаемые поглотители (SESAM) использовались для синхронизации мод лазера еще в 1974 году, когда р-тип германий использовался для блокировки режима CO2 лазер который генерировал импульсы ~ 500 пс. Современные SESAM Полупроводник III-V одиночная квантовая яма (SQW) или несколько квантовых ям (MQW), выращенные на полупроводнике распределенные брэгговские отражатели (DBR). Первоначально они использовались в схеме резонансной импульсной синхронизации (RPM) в качестве пусковых механизмов для Ti: сапфировые лазеры в котором KLM использовался в качестве быстро насыщающегося поглотителя. RPM - еще один метод синхронизации мод со связанными резонаторами. В отличие от лазеров APM, которые используют нерезонансную фазовую нелинейность типа Керра для сокращения импульсов, RPM использует нелинейность амплитуды, обеспечиваемую эффектами резонансного заполнения зон полупроводников. Вскоре SESAM были преобразованы во внутрирезонаторные насыщаемые поглотители из-за большей простоты, присущей этой структуре. С тех пор использование SESAM позволило определить длительность импульса, среднюю мощность, энергию импульса и частоту повторения сверхбыстрый твердотельные лазеры должно быть улучшено на несколько порядков. Получены средняя мощность 60 Вт и частота следования до 160 ГГц. При использовании KLM с поддержкой SESAM были получены импульсы длительностью менее 6 фс непосредственно от Ti: сапфирового генератора. Основное преимущество SESAM по сравнению с другими методами насыщения поглотителя заключается в том, что параметрами поглотителя можно легко управлять в широком диапазоне значений. Например, флюенс насыщения можно контролировать, изменяя отражательная способность верхнего отражателя, покаглубина модуляции и время восстановления могут быть адаптированы путем изменения низкотемпературных условий выращивания абсорбирующих слоев. Эта свобода дизайна еще больше расширила применение SESAM для синхронизации мод. волоконные лазеры где требуется относительно высокая глубина модуляции для обеспечения самозапуска и стабильности работы. Успешно были продемонстрированы волоконные лазеры, работающие на диапазонах ~ 1 мкм и 1,5 мкм.[9]
Термоэлектрики
Квантовые ямы оказались многообещающими для сбора энергии, поскольку термоэлектрический устройств. Утверждается, что их проще изготовить и они могут работать при комнатной температуре. Скважины соединяют центральную полость с двумя электронными резервуарами. В центральной полости поддерживается более высокая температура, чем в резервуарах. Ямки действуют как фильтры, которые пропускают электроны определенных энергий. Как правило, большая разница температур между резонатором и резервуарами увеличивает поток электронов и выходную мощность.[10][11]
Экспериментальный прибор обеспечивал выходную мощность около 0,18 Вт / см.2 при разнице температур в 1 K это почти вдвое больше, чем у накопителя энергии с квантовыми точками. Дополнительные степени свободы допускали большие токи. Его эффективность немного ниже, чем у сборщиков энергии с квантовыми точками. Квантовые ямы пропускают электроны любой энергии выше определенного уровня, а квантовые точки пропускают только электроны определенной энергии.[10]
Одно из возможных приложений - преобразовать отходящее тепло из электрических цепей, например, в компьютерных микросхемах, обратно в электричество, уменьшая потребность в охлаждении и энергии для питания микросхемы.[10]
Солнечные батареи
Квантовые ямы были предложены для повышения эффективности солнечные батареи. Теоретическая максимальная эффективность традиционных однопереходных ячеек составляет около 34%, в значительной степени из-за их неспособности улавливать много разных длин волн света. Многопереходные солнечные элементы, которые состоят из нескольких последовательно соединенных p-n переходов с разными запрещенными зонами, повышают теоретическую эффективность за счет расширения диапазона поглощаемых длин волн, но их сложность и стоимость изготовления ограничивают их использование нишевыми приложениями. С другой стороны, ячейки, состоящие из p-i-n-перехода, в котором собственная область содержит одну или несколько квантовых ям, приводят к увеличению фототока по сравнению с темновым током, что приводит к увеличению чистой эффективности по сравнению с обычными p-n-ячейками.[12] Фотоны энергии в глубине ямы поглощаются в ямах и генерируют электронно-дырочные пары. В условиях комнатной температуры эти фотогенерируемые носители обладают достаточной тепловой энергией, чтобы покинуть скважину быстрее, чем скорость рекомбинации.[13] Продуманные многопереходные солнечные элементы с квантовыми ямами могут быть изготовлены с использованием методов послойного осаждения, таких как молекулярно-лучевая эпитаксия или химическое осаждение из паровой фазы. Также было показано, что металлические или диэлектрические наночастицы, добавленные над ячейкой, приводят к дальнейшему увеличению фотопоглощения за счет рассеяния падающего света на боковые пути распространения, ограниченные внутренним слоем с множеством квантовых ям.[14]
Однопереходные солнечные элементы
В обычных однопереходных фотоэлектрических солнечных элементах генерируемая мощность является произведением фототока и напряжения на диоде.[15] Поскольку полупроводники поглощают только фотоны с энергией, превышающей их ширину запрещенной зоны, материал с меньшей шириной запрещенной зоны поглощает большую часть спектра солнечного излучения, что приводит к большему току. Наибольшее достижимое напряжение холостого хода - это ширина запрещенной зоны материала.[15] Поскольку запрещенная зона полупроводника определяет как ток, так и напряжение, проектирование солнечного элемента всегда представляет собой компромисс между максимальным выходом тока с малой шириной запрещенной зоны и выходным напряжением с большой шириной запрещенной зоны.[16] Максимальный теоретический предел эффективности для обычных солнечных элементов определен на уровне всего 31%, а для лучших кремниевых устройств оптимальный предел составляет 25%.[15]
С введением квантовых ям (КЯ) предел эффективности кремниевых устройств с однопереходными напряженными КЯ увеличился до 28,3%.[15] Увеличение происходит из-за ширины запрещенной зоны барьерного материала, определяющей встроенное напряжение. Тогда как ширина запрещенной зоны квантовых ям теперь определяет предел поглощения.[15] В своих экспериментах с фотодиодами на p-i-n-переходе группа Барнхема показала, что размещение квантовых ям в обедненной области увеличивает эффективность устройства.[17] Исследователи делают вывод, что результирующее увеличение указывает на то, что генерация новых носителей и фототока из-за включения более низких энергий в спектр поглощения перевешивает падение напряжения на клеммах в результате рекомбинации носителей, захваченных в квантовых ямах. Дальнейшие исследования позволили сделать вывод, что увеличение фототока напрямую связано с красным смещением спектра поглощения.[17]
Многопереходные солнечные элементы
В настоящее время среди солнечных элементов без QW многопереходные солнечные элементы III / V являются наиболее эффективными, обеспечивая максимальную эффективность 46% при высокой концентрации солнечного света. Многопереходные солнечные элементы создаются путем наложения нескольких p-i-n переходов с разными запрещенными зонами.[8] Эффективность солнечного элемента увеличивается с включением большего количества солнечного излучения в спектр поглощения за счет введения большего количества квантовых ям с различными запрещенными зонами. Прямая связь между шириной запрещенной зоны и постоянной решетки препятствует развитию многопереходных солнечных элементов. По мере роста количества квантовых ям (КЯ) материал растет вместе с дислокациями из-за различных постоянных решетки. Дислокации уменьшают диффузионную длину и время жизни носителей.[8] Следовательно, квантовые ямы представляют собой альтернативный подход к многопереходным солнечным элементам с минимальной кристаллической дислокацией.
Энергия запрещенной зоны
Исследователи стремятся использовать квантовые ямы для выращивания высококачественного материала с минимальными кристаллическими дислокациями и повышения эффективности поглощения света и сбора носителей для получения более эффективных солнечных элементов с квантовыми ямами. Возможность настройки ширины запрещенной зоны помогает исследователям при проектировании солнечных элементов. Мы можем оценить эффективную запрещенная зона как функция ширины запрещенной зоны квантовой ямы и сдвига в запрещенной зоне из-за стерической деформации: квантовый эффект Штарка (QCSE) и квантовый размерный эффект (QSE).[8]
Деформация материала вызывает два эффекта в запрещенной зоне. Во-первых, это изменение относительной энергии зоны проводимости и валентной зоны. На это изменение энергии влияет напряжение, , коэффициенты упругой жесткости, и , и потенциал гидростатической деформации, .[8][18]
Во-вторых, из-за деформации происходит расщепление вырождения тяжелых и легких дырок. В сильно сжатом материале тяжелые дыры (чч) перейти в более высокое энергетическое состояние. В растяжимом материале легкие дырочки (lh) перейти в более высокое энергетическое состояние. [8] [19] Можно вычислить разницу в энергии за счет расщепления чч и lh от потенциала деформации сдвига, , напряжение, коэффициенты упругой жесткости и .[19]
В квантовое ограничение эффект Штарка вызывает сдвиг запрещенной зоны в зависимости от толщины скважины. Если это элементарный заряд; и - эффективная ширина квантовых ям в зоне проводимости и валентной зоне соответственно; - индуцированное электрическое поле, обусловленное пьезоэлектрической и спонтанной поляризацией; и - приведенная постоянная Планка, то сдвиг энергии равен:[8]
Квантовый размерный эффект (QSE) - это дискретизация энергии, которой подвергается носитель заряда из-за ограничения, когда его Радиус Бора больше размера колодца. По мере увеличения толщины квантовой ямы КРС уменьшаются. Уменьшение QSE вызывает состояние, чтобы сместиться вниз и уменьшить эффективную запрещенную зону.[8] В Модель Кронига – Пенни используется для вычисления квантовых состояний[20], и Правило Андерсона применяется для оценки смещения зоны проводимости и валентной зоны по энергии.[21]

Захват носителя и срок службы
Благодаря эффективному использованию носителей в квантовых ямах исследователи могут повысить эффективность солнечных элементов с квантовыми ямами (QWSC). В квантовых ямах во внутренней области солнечных элементов p-i-n оптически генерируемые носители либо собираются встроенным полем, либо теряются из-за рекомбинации носителей. [8] Рекомбинация носителей это процесс, в котором дырка и электрон рекомбинируют, чтобы нейтрализовать свои заряды. Носители могут собираться дрейфом под действием электрического поля. Можно использовать либо тонкие ямы и транспортные носители посредством термоэлектронной эмиссии, либо тонкие барьеры и транспортные носители посредством туннелирования.
Время жизни носителя для выхода определяется временем жизни туннелирования и термоэлектронной эмиссии. Время жизни туннелирования и термоэлектронной эмиссии зависит от низкой эффективной высоты барьера. Они выражаются следующими уравнениями[8][22]:
- ,
где и - эффективные массы носителей заряда в барьере и хорошо, - эффективная высота барьера, а - электрическое поле.
Тогда можно рассчитать время жизни побега следующим образом:[8][22]:
Полная вероятность выхода неосновных носителей заряда из квантовых ям складывается из вероятностей каждой ямы,
- .[22]
Вот, ,[22], где время рекомбинации, и - полное количество квантовых ям в собственной области.
Для , высока вероятность запоминания несущей. Предположения, сделанные в этом методе моделирования, заключаются в том, что каждый носитель пересекает КЯ, тогда как на самом деле они пересекают разное количество КЯ и захват носителей составляет 100%, что может быть неверным в условиях высокого фонового легирования.[8]
Например, принимая In0.18Ga0.82Как (125) / GaAs0.36п0.64 (40) время жизни туннелирования и термоэлектронной эмиссии составляет 0,89 и 1,84 соответственно. Даже если принять время рекомбинации 50 нс, вероятность выхода из одной квантовой ямы и 100 квантовых ям составляет 0,984 и 0,1686, что недостаточно для эффективного захвата носителей.[8] Уменьшение толщины барьера до 20 Ангстрем снижает до 4,1276 пс, увеличивая вероятность ухода на 100 квантовых ям до 0,9918. Это указывает на то, что использование тонких барьеров необходимо для более эффективного сбора носителей.[8]
Устойчивость устройств с квантовыми ямами по сравнению с объемным материалом с точки зрения производительности
В диапазоне 1,1–1,3 эВ Sayed et al.[8] сравнивает внешняя квантовая эффективность (EQE) метаморфной объемной субэлемента InGaAs на подложках Ge от Spectrolab[23] до 100-периодного В0.30Ga0.70As (3,5 нм) / GaAs (2,7 нм) / GaAs0.60п0.40(3,0 нм) QWSC от Fuji et al.[24]. Объемный материал показывает более высокие значения EQE, чем QW в области 880-900 нм, тогда как QW имеют более высокие значения EQE в диапазоне 400-600 нм.[8] Этот результат дает некоторое свидетельство того, что существует борьба за расширение пороговых значений поглощения квантовых ям до более длинных волн из-за проблем баланса деформации и транспорта носителей. Однако объемный материал имеет больше деформаций, что приводит к меньшему времени жизни неосновных носителей заряда. [8]
В диапазоне 1,6–1,8 согласованный по решетке AlGaAs Хекельманом и др.[25] и InGaAsP от Jain et al.[26] сравниваются Сайедом[8] с согласованной по решетке структурой квантовых ям InGaAsP / InGaP Сайеда и др.[27]. Как и в диапазоне 1,1–1,3 эВ, EQE массивного материала выше в более длинноволновой области спектра, но квантовые ямы имеют преимущество в том смысле, что они поглощают более широкую область спектра. Кроме того, его можно выращивать при более низких температурах, предотвращая термическую деградацию.[8]
Применение квантовых ям во многих устройствах является жизнеспособным решением для повышения энергоэффективности таких устройств. В случае лазеров улучшение уже привело к значительным результатам, таким как светодиоды. С помощью QWSC сбор энергии от солнца становится более мощным методом выращивания энергии, поскольку они способны поглощать больше солнечного излучения и более эффективно улавливать такую энергию от носителей заряда. Жизнеспособный вариант, такой как QWSCs, предоставляет общественности возможность перейти от методов, вызывающих парниковый эффект, к более зеленой альтернативе - солнечной энергии.
Смотрите также
- Частица в коробке
- Квантовая проволока, носители ограничены в двух измерениях.
- Квантовая точка, носители ограничены во всех трех измерениях.
- Лазер на квантовой яме
- Модулирующий светоотражатель
использованная литература
- ^ "Инфракрасные фотонные детекторы с квантовыми ямами | IRnova". www.ir-nova.se. Получено 2018-09-04.
- ^ а б Одох, Э. О., & Нджапба, А. С. (2015). Обзор полупроводниковых устройств с квантовыми ямами. Adv. Phys. Теор. Приложение, 46, 26-32.
- ^ Кремер, Х. (1963). «Предлагаемый класс инжекционных лазеров на гетеропереходах». Труды IEEE. Институт инженеров по электротехнике и радиоэлектронике (IEEE). 51 (12): 1782–1783. Дои:10.1109 / proc.1963.2706. ISSN 0018-9219.
- ^ Ж. И. Алферов, Р.Ф. Казаринов, Авторское свидетельство 28448 (СССР) 1963.
- ^ а б c d е ж г час я Фокс, Марк; Ispasoiu, Radu (2006), "Квантовые ямы, сверхрешетки и инженерия запрещенной зоны", Справочник Springer по электронным и фотонным материалам, Springer, США, стр. 1021–1040, Дои:10.1007/978-0-387-29185-7_42, ISBN 978-0-387-26059-4
- ^ а б Наг, Б. Р. (2002). Физика устройств с квантовыми ямами. Kluwer Academic Publishers. OCLC 754036669.
- ^ а б Саймон, Стивен Х. (2017). Основы оксфордского твердого тела. Издательство Оксфордского университета. ISBN 978-0-19-968077-1. OCLC 1091723162.
- ^ а б c d е ж г час я j k л м п о п q р s т ты v Саид, Ислам; Бедайр, С. М. (2 марта 2019 г.). «Солнечные элементы с квантовыми ямами: принципы, последние достижения и потенциал». Журнал IEEE по фотогальванике. 9 (2): 402–423. Дои:10.1109 / JPHOTOV.2019.2892079. ISSN 2156-3381. S2CID 67874610.
- ^ Tang, D .; Zhang, H .; Zhao, L .; Ву, X. (2008). «Наблюдение векторных солитонов высокого порядка с синхронизацией по поляризации в волоконном лазере» (PDF). Письма с физическими проверками. 101 (15): 153904. arXiv:0903.2392. Bibcode:2008PhRvL.101o3904T. Дои:10.1103 / PhysRevLett.101.153904. PMID 18999601. S2CID 35230072. Архивировано из оригинал (PDF) 20 января 2010 г.
- ^ а б c «Ученые предлагают квантовые ямы в качестве мощных и простых в изготовлении сборщиков энергии». Phys.org. Получено 2013-10-24.
- ^ Sothmann, B.R .; Sánchez, R .; Jordan, A. N .; Бюттикер, М. (2013). «Мощный накопитель энергии на основе резонансно-туннельных квантовых ям». Новый журнал физики. 15 (9): 095021. arXiv:1309.7907. Bibcode:2013NJPh ... 15i5021S. Дои:10.1088/1367-2630/15/9/095021. S2CID 119210320.
- ^ Barnham, K .; Захариу, А. (1997). «Солнечные элементы с квантовыми ямами». Прикладная наука о поверхности. 113-114: 722–733. Bibcode:1997ApSS..113..722B. Дои:10.1016 / S0169-4332 (96) 00876-8.
- ^ Ramey, S.M .; Хойе, Р. (2003). «Моделирование солнечных элементов с несколькими квантовыми ямами, включая захват, ускользание и рекомбинацию фотовозбужденных носителей в квантовых ямах». Транзакции IEEE на электронных устройствах. 50 (5): 1179–1188. Bibcode:2003ITED ... 50.1179R. Дои:10.1109 / TED.2003.813475.
- ^ Derkacs, D .; Chen, W. V .; Matheu, P.M .; Lim, S. H .; Ю., П. К. Л .; Ю., Э. Т. (2008). «Рассеяние света, вызванное наночастицами, для улучшения характеристик солнечных элементов с квантовыми ямами». Письма по прикладной физике. 93 (9): 091107. Bibcode:2008АпФЛ..93и1107Д. Дои:10.1063/1.2973988.
- ^ а б c d е Фокс, Марк; Ispasoiu, Radu (2017), Kasap, Safa; Кэппер, Питер (ред.), "Квантовые ямы, сверхрешетки и инженерия запрещенной зоны", Справочник Springer по электронным и фотонным материалам, Springer International Publishing, стр. 1, Дои:10.1007/978-3-319-48933-9_40, ISBN 978-3-319-48931-5
- ^ Барнем, Кейт; Баллард, Ян; Барнс, Дженни; Коннолли, Джеймс; Гриффин, Пол; Клуфтингер, Бенджамин; Нельсон, Дженни; Цуй, Эрнест; Захариу, Александр (1 апреля 1997 г.). «Солнечные элементы с квантовыми ямами». Прикладная наука о поверхности. Материалы восьмой Международной конференции по твердым пленкам и поверхностям. 113-114: 722–733. Bibcode:1997ApSS..113..722B. Дои:10.1016 / S0169-4332 (96) 00876-8. ISSN 0169-4332.
- ^ а б Андерсон, Нил Г. (13 апреля 1995 г.). «Идеальная теория солнечных элементов с квантовыми ямами». Журнал прикладной физики. 78 (3): 1850–1861. Bibcode:1995JAP .... 78.1850A. Дои:10.1063/1.360219. ISSN 0021-8979.
- ^ Асаи, Хиромицу; Оэ, Кунисигэ (1983). «Сдвиг запрещенной зоны при упругой деформации в эпитаксиальных слоях GaxIn1-xP на подложках (001) GaAs». Журнал прикладной физики. 54 (4): 2052–2056. Дои:10.1063/1.332252. ISSN 0021-8979.
- ^ а б Адачи, Садао (1982). «Материальные параметры In1-xGaxAsyP1-y и связанных двоичных файлов». Журнал прикладной физики. 53 (12): 8775–8792. Дои:10.1063/1.330480. ISSN 0021-8979.
- ^ «Квантовые проволоки и точки», Квантовые ямы, проволоки и точки, John Wiley & Sons, Ltd, 2006-01-27, стр. 243–270, Дои:10.1002 / 0470010827.ch8, ISBN 978-0-470-01082-2
- ^ Андерсон, Р. Л. (1960). «Гетеропереходы арсенида германия и галлия [письмо в редакцию]». Журнал исследований и разработок IBM. 4 (3): 283–287. Дои:10.1147 / ряд 43.0283. ISSN 0018-8646.
- ^ а б c d Nelson, J .; Paxman, M .; Barnham, K.W.J .; Roberts, J.S .; Баттон, К. (июнь 1993 г.). «Устойчивый выход носителей из одиночных квантовых ям». Журнал IEEE по квантовой электронике. 29 (6): 1460–1468. Bibcode:1993IJQE ... 29.1460N. Дои:10.1109/3.234396. ISSN 0018-9197.
- ^ Кинг, Р., Лоу, Д., Фетцер, К., Шериф, Р., Эдмондсон, К., Курц, С., ... и Карам, Н. Х. (2005, июнь). Пути к созданию фотоэлектрических концентраторов с КПД 40%. В Proc. 20-я Европейская конференция по фотоэлектрической солнечной энергии (стр. 10-11).
- ^ Фудзи, Хиромаса; Топрасертпонг, Касидит; Ван, Юньпэн; Ватанабе, Кентарох; Сугияма, Масакадзу; Накано, Ёсиаки (2014). «100-периодные квантовые ямы InGaAs / GaAsP с шириной запрещенной зоны 1,23 эВ для высокоэффективных GaAs солнечных элементов: к тандемным элементам на основе Ge с согласованием по току». Прогресс в фотоэлектрической технике: исследования и приложения. 22 (7): 784–795. Дои:10.1002 / пункт. 2454.
- ^ Хекельманн, Стефан; Лакнер, Дэвид; Керхер, Кристиан; Димрот, Франк; Бетт, Андреас В. (2015). "Расследование на АлИксGa1-хКак солнечные элементы, выращенные МОВПЭ ». Журнал IEEE по фотогальванике. 5 (1): 446–453. Дои:10.1109 / jphotov.2014.2367869. S2CID 41026351.
- ^ Джайн, никхил; Geisz, Джон Ф .; Франция, Райан М .; Норман, Эндрю Дж .; Штайнер, Майлс А. (2017). "Повышенный токосъем в солнечных элементах на основе GaInAsP 1,7 эВ, выращенных на GaAs методом парофазной эпитаксии из металлоорганических соединений". Журнал IEEE по фотогальванике. 7 (3): 927–933. Дои:10.1109 / jphotov.2017.2655035. OSTI 1360894. S2CID 20841656.
- ^ Сайед, Ислам Э. Х .; Джайн, никхил; Steiner, Myles A .; Geisz, Джон Ф .; Бедайр, С. М. (2017). «100-периодный солнечный элемент на сверхрешетке InGaAsP / InGaP с субзонной квантовой эффективностью, приближающейся к 80%». Письма по прикладной физике. 111 (8): 082107. Bibcode:2017АпФЛ.111х2107С. Дои:10.1063/1.4993888. OSTI 1393377.
дальнейшее чтение
- Томас Энгель, Филип Рид Квантовая химия и спектроскопия. ISBN 0-8053-3843-8. Pearson Education, 2006. Страницы 73–75.


















































