Вырожденные уровни энергии - Degenerate energy levels - Wikipedia

Эта статья о разных квантовых состояниях с одинаковой энергией. Для использования в других целях см. Вырождение.

Сюда перенаправляется «квантовое вырождение». Иногда это относится к дегенеративная материя.

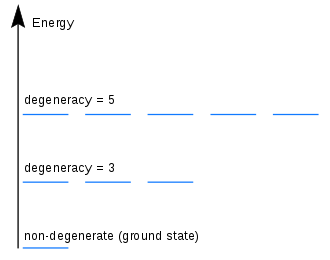
В квантовая механика, уровень энергии является выродиться если он соответствует двум или более различным измеримым состояниям квантовая система. И наоборот, два или более различных состояния квантово-механической системы называются вырожденными, если при измерении они дают одинаковое значение энергии. Количество различных состояний, соответствующих определенному уровню энергии, известно как степень вырождения уровня. Математически он представлен Гамильтониан для системы, имеющей более одного линейно независимый собственное состояние с той же энергией собственное значение.^{[1]:п. 48} В этом случае одной энергии недостаточно, чтобы охарактеризовать, в каком состоянии находится система, а другие квантовые числа необходимы для точной характеристики состояния, когда желательно различение. В классическая механика, это можно понять в терминах различных возможных траекторий, соответствующих одной и той же энергии.

Вырождение играет фундаментальную роль в квантовая статистическая механика. Для N-частичной системы в трех измерениях, один энергетический уровень может соответствовать нескольким различным волновым функциям или энергетическим состояниям. Все эти вырожденные состояния на одном уровне с равной вероятностью могут быть заполнены. Количество таких состояний дает вырождение того или иного уровня энергии.

Вырожденные состояния в квантовой системе

Математика

Возможные состояния квантово-механической системы можно рассматривать математически как абстрактные векторы в разделимом, сложном Гильбертово пространство, в то время как наблюдаемые может быть представлен линейный Эрмитовы операторы действуя на них. Выбрав подходящий основа, компоненты этих векторов и матричные элементы операторов в этом базисе могут быть определены. Если А это N × N матрица Икс ненулевой вектор, и λ это скаляр, так что ${\displaystyle AX=\lambda X}$, то скаляр λ называется собственным значением А и вектор Икс называется собственным вектором, соответствующим λ. Вместе с нулевым вектором множество всех собственные векторы соответствующий заданному собственному значению λ сформировать подпространство из ℂ^п, который называется собственное подпространство из λ. Собственное значение λ который соответствует двум или более различным линейно независимым собственным векторам, называется выродиться, т.е. ${\displaystyle AX_{1}=\lambda X_{1}}$ и ${\displaystyle AX_{2}=\lambda X_{2}}$, куда ${\displaystyle X_{1}}$ и ${\displaystyle X_{2}}$ являются линейно независимыми собственными векторами. В измерение собственного подпространства, соответствующего этому собственному значению, называется его степень вырождения, которые могут быть конечными или бесконечными. Собственное значение называется невырожденным, если его собственное подпространство одномерно.

Собственные значения матриц, представляющих физические наблюдаемые в квантовая механика дают измеримые значения этих наблюдаемых, в то время как собственные состояния, соответствующие этим собственным значениям, дают возможные состояния, в которых система может находиться после измерения. Измеримые значения энергии квантовой системы задаются собственными значениями оператора Гамильтона, а его собственные состояния дают возможные энергетические состояния системы. Значение энергии называется вырожденным, если существует по крайней мере два линейно независимых энергетических состояния, связанных с ним. Более того, любые линейная комбинация двух или более вырожденных собственных состояний также является собственным состоянием оператора Гамильтона, соответствующего одному и тому же собственному значению энергии. Это ясно следует из того, что собственное подпространство собственного значения значения энергии λ является подпространством (являясь ядро гамильтониана минус λ умноженное на единицу), следовательно, замкнуто относительно линейных комбинаций.

Доказательство приведенной выше теоремы.[2]:п. 52

Если ${\displaystyle {\hat {H}}}$ представляет Гамильтониан оператор и ${\displaystyle |\psi _{1}\rangle }$ и ${\displaystyle |\psi _{2}\rangle }$ два собственных состояния, соответствующие одному и тому же собственному значению E, тогда ${\displaystyle {\hat {H}}|\psi _{1}\rangle =E|\psi _{1}\rangle }$ ${\displaystyle {\hat {H}}|\psi _{2}\rangle =E|\psi _{2}\rangle }$ Позволять ${\displaystyle |\psi \rangle =c_{1}|\psi _{1}\rangle +c_{2}|\psi _{2}\rangle }$, куда ${\displaystyle c_{1}}$ и ${\displaystyle c_{2}}$ комплексные (в общем случае) константы, любая линейная комбинация ${\displaystyle |\psi _{1}\rangle }$ и ${\displaystyle |\psi _{2}\rangle }$.Потом, ${\displaystyle {\hat {H}}|\psi \rangle ={\hat {H}}(c_{1}|\psi _{1}\rangle +c_{2}|\psi _{2}\rangle )}$ ${\displaystyle =c_{1}{\hat {H}}|\psi _{1}\rangle +c_{2}{\hat {H}}|\psi _{2}\rangle }$ ${\displaystyle =E(c_{1}|\psi _{1}\rangle +c_{2}|\psi _{2}\rangle )}$ ${\displaystyle =E|\psi \rangle }$ что показывает, что ${\displaystyle |\psi \rangle }$ является собственным состоянием ${\displaystyle {\hat {H}}}$ с тем же собственным значением E.

Влияние вырождения на измерение энергии

При отсутствии вырождения, если измеренное значение энергии квантовой системы определяется, соответствующее состояние системы считается известным, поскольку каждому собственному значению энергии соответствует только одно собственное состояние. Однако если гамильтониан ${\displaystyle {\hat {H}}}$ имеет вырожденное собственное значение ${\displaystyle E_{n}}$ степени g_п, связанные с ним собственные состояния образуют векторное подпространство из измерение грамм_п. В таком случае несколько конечных состояний могут быть связаны с одним и тем же результатом. ${\displaystyle E_{n}}$, все из которых являются линейными комбинациями g_п ортонормированный собственные векторы ${\displaystyle |E_{n,i}\rangle }$.

В этом случае вероятность того, что значение энергии, измеренное для системы в состоянии ${\displaystyle |\psi \rangle }$ даст значение${\displaystyle E_{n}}$ дается суммой вероятностей нахождения системы в каждом из состояний в этом базисе, т.е.

${\displaystyle P(E_{n})=\sum _{i=1}^{g_{n}}|\langle E_{n,i}|\psi \rangle |^{2}}$

Вырождение в разных измерениях

Этот раздел призван проиллюстрировать существование вырожденных уровней энергии в квантовых системах, изучаемых в различных измерениях. Изучение одно- и двумерных систем помогает концептуальному пониманию более сложных систем.

Вырождение в одном измерении

В некоторых случаях аналитический легче получить результаты при изучении одномерных систем. Для квантовой частицы с волновая функция ${\displaystyle |\psi \rangle }$ движется в одномерном потенциале ${\displaystyle V(x)}$, то не зависящее от времени уравнение Шредингера можно записать как

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}+V\psi =E\psi }$

Поскольку это обыкновенное дифференциальное уравнение, существуют две независимые собственные функции для данной энергии ${\displaystyle E}$ самое большее, так что степень вырождения никогда не превышает двух. Можно доказать, что в одном измерении не существует вырожденных связанные состояния за нормируемые волновые функции. Достаточное условие на кусочно-непрерывный потенциал ${\displaystyle V}$ и энергия ${\displaystyle E}$ существует два действительных числа ${\displaystyle M,x_{0}}$ с ${\displaystyle M\neq 0}$ такой, что ${\displaystyle \forall x>x_{0}}$ у нас есть ${\displaystyle V(x)-E\geq M^{2}}$.^[3] Особенно, ${\displaystyle V}$ ограничена снизу по этому критерию.

Доказательство приведенной выше теоремы.

Рассмотрение одномерной квантовой системы в потенциале ${\displaystyle V(x)}$ с вырожденными состояниями ${\displaystyle |\psi _{1}\rangle }$ и ${\displaystyle |\psi _{2}\rangle }$ соответствующему тому же собственному значению энергии ${\displaystyle E}$, записав не зависящее от времени уравнение Шредингера для системы: ${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi _{1}}{dx^{2}}}+V\psi _{1}=E\psi _{1}}$ ${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi _{2}}{dx^{2}}}+V\psi _{2}=E\psi _{2}}$ Умножая первое уравнение на ${\displaystyle \psi _{2}}$ а второй ${\displaystyle \psi _{1}}$ и вычитая одно из другого, получаем: ${\displaystyle \psi _{1}{\frac {d^{2}}{dx^{2}}}\psi _{2}-\psi _{2}{\frac {d^{2}}{dx^{2}}}\psi _{1}=0}$ Объединение обеих сторон ${\displaystyle \psi _{1}{\frac {d\psi _{2}}{dx}}-\psi _{2}{\frac {d\psi _{1}}{dx}}={\mbox{constant}}}$ В случае хорошо определенных и нормируемых волновых функций указанная выше постоянная обращается в нуль, если обе волновые функции обращаются в нуль хотя бы в одной точке, и мы находим:${\displaystyle \psi _{1}(x)=c\psi _{2}(x)}$куда ${\displaystyle c}$ в общем случае является комплексной константой. Для связанного состояния собственные функции (которые стремятся к нулю при ${\displaystyle x\rightarrow \infty }$), и полагая ${\displaystyle V}$ и ${\displaystyle E}$ удовлетворяют приведенному выше условию, можно показать[3] что также первая производная волновой функции стремится к нулю в пределе ${\displaystyle x\to \infty }$, так что указанная константа равна нулю и у нас нет вырождения.

Вырождение в двумерных квантовых системах

Двумерные квантовые системы существуют во всех трех состояниях материи, и большая часть разнообразия, наблюдаемого в трехмерной материи, может быть создана в двух измерениях. Настоящие двухмерные материалы состоят из одноатомных слоев на поверхности твердых тел. Некоторые примеры двумерных электронных систем, полученных экспериментально, включают: МОП-транзистор, двумерный сверхрешетки из Гелий, Неон, Аргон, Ксенон и т. д. и поверхность жидкий гелий. Наличие вырожденных уровней энергии исследуется в случаях частицы в ящике и двумерной гармонический осциллятор, которые действуют как полезные математические модели для нескольких систем реального мира.

Частица в прямоугольной плоскости

Рассмотрим свободную частицу в плоскости измерений ${\displaystyle L_{x}}$ и ${\displaystyle L_{y}}$ в плоскости непроницаемых стен. Не зависящее от времени уравнение Шредингера для этой системы с волновой функцией ${\displaystyle |\psi \rangle }$ можно записать как

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{{\partial x}^{2}}}+{\frac {\partial ^{2}\psi }{{\partial y}^{2}}}\right)=E\psi }$

Допустимые значения энергии:

${\displaystyle E_{n_{x},n_{y}}={\frac {\pi ^{2}\hbar ^{2}}{2m}}\left({\frac {n_{x}^{2}}{L_{x}^{2}}}+{\frac {n_{y}^{2}}{L_{y}^{2}}}\right)}$

Нормированная волновая функция

${\displaystyle \psi _{n_{x},n_{y}}(x,y)={\frac {2}{\sqrt {L_{x}L_{y}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{y}}}\right)}$

куда ${\displaystyle n_{x},n_{y}=1,2,3...}$

Так, квантовые числа ${\displaystyle n_{x}}$ и ${\displaystyle n_{y}}$ требуются для описания собственных значений энергии, а наименьшая энергия системы определяется выражением

${\displaystyle E_{1,1}=\pi ^{2}{\frac {\hbar ^{2}}{2m}}\left({\frac {1}{L_{x}^{2}}}+{\frac {1}{L_{y}^{2}}}\right)}$

Для некоторых соизмеримых соотношений двух длин ${\displaystyle L_{x}}$ и ${\displaystyle L_{y}}$, некоторые пары состояний вырождены. Если ${\displaystyle L_{x}/L_{y}=p/q}$, где p и q - целые числа, состояния ${\displaystyle (n_{x},n_{y})}$ и ${\displaystyle (pn_{y}/q,qn_{x}/p)}$ имеют одинаковую энергию и поэтому вырождены друг к другу.

Частица в квадратном ящике

В этом случае габариты коробки ${\displaystyle L_{x}=L_{y}=L}$ а собственные значения энергии даются

${\displaystyle E_{n_{x},n_{y}}={\frac {\pi ^{2}\hbar ^{2}}{2mL^{2}}}(n_{x}^{2}+n_{y}^{2})}$

С ${\displaystyle n_{x}}$ и ${\displaystyle n_{y}}$ можно менять местами без изменения энергии, каждый энергетический уровень имеет вырождение не менее двух, когда ${\displaystyle n_{x}}$ и ${\displaystyle n_{y}}$ разные. Вырожденные состояния также получаются, когда сумма квадратов квантовых чисел, соответствующих различным уровням энергии, одинакова. Например, три состояния (n_Икс = 7, п_у = 1), (n_Икс = 1, n_у = 7) и (n_Икс = п_у = 5) у всех есть ${\displaystyle E=50{\frac {\pi ^{2}\hbar ^{2}}{2mL^{2}}}}$ и составляют вырожденное множество.

Степени вырождения разных уровней энергии для частицы в квадратном ящике:

${\displaystyle n_{x}}$	${\displaystyle n_{y}}$	${\displaystyle E\left({\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\right)}$	Вырождение
1	1	2	1
2 1	1 2	5 5	2
2	2	8	1
3 1	1 3	10 10	2
3 2	2 3	13 13	2
4 1	1 4	17 17	2
3	3	18	1

Частица в кубической коробке

В этом случае габариты коробки ${\displaystyle L_{x}=L_{y}=L_{z}=L}$ а собственные значения энергии зависят от трех квантовых чисел.

${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\pi ^{2}\hbar ^{2}}{2mL^{2}}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})}$

С ${\displaystyle n_{x}}$, ${\displaystyle n_{y}}$ и ${\displaystyle n_{z}}$ можно поменять местами без изменения энергии, каждый энергетический уровень имеет вырождение не менее трех, когда не все три квантовых числа равны.

Нахождение уникального собственного базиса в случае вырождения

Если два операторы ${\displaystyle {\hat {A}}}$ и ${\displaystyle {\hat {B}}}$ добираться, т.е. ${\displaystyle [{\hat {A}},{\hat {B}}]=0}$, то для каждого собственного вектора ${\displaystyle |\psi \rangle }$ из ${\displaystyle {\hat {A}}}$, ${\displaystyle {\hat {B}}|\psi \rangle }$ также является собственным вектором ${\displaystyle {\hat {A}}}$ с тем же собственным значением. Однако, если это собственное значение, скажем ${\displaystyle \lambda }$, является вырожденным, можно сказать, что ${\displaystyle {\hat {B}}|\psi \rangle }$ принадлежит собственному подпространству ${\displaystyle E_{\lambda }}$ из ${\displaystyle {\hat {A}}}$, который называется глобально инвариантным относительно действия ${\displaystyle {\hat {B}}}$.

Для двух перемещающихся наблюдаемых А и B, можно построить ортонормированный базис пространства состояний с собственными векторами, общими для двух операторов. Тем не мение, ${\displaystyle \lambda }$ является вырожденным собственным значением ${\displaystyle {\hat {A}}}$, то это собственное подпространство ${\displaystyle {\hat {A}}}$ инвариантный под действием ${\displaystyle {\hat {B}}}$, Итак представление из ${\displaystyle {\hat {B}}}$ на собственной основе ${\displaystyle {\hat {A}}}$ не диагональ, а блочно-диагональная матрица, т.е. вырожденные собственные векторы ${\displaystyle {\hat {A}}}$ не являются, вообще говоря, собственными векторами ${\displaystyle {\hat {B}}}$. Однако всегда можно выбрать в каждом вырожденном собственном подпространстве ${\displaystyle {\hat {A}}}$, базис из собственных векторов, общих для ${\displaystyle {\hat {A}}}$ и ${\displaystyle {\hat {B}}}$.

Выбор полного набора коммутирующих наблюдаемых

Если данная наблюдаемая А невырожден, существует единственный базис, образованный его собственными векторами. С другой стороны, если одно или несколько собственных значений ${\displaystyle {\hat {A}}}$ являются вырожденными, задание собственного значения недостаточно для характеристики базисного вектора. Если, выбирая наблюдаемую ${\displaystyle {\hat {B}}}$, который курсирует с ${\displaystyle {\hat {A}}}$, можно построить ортонормированный базис собственных векторов, общих для ${\displaystyle {\hat {A}}}$ и ${\displaystyle {\hat {B}}}$, который уникален для каждой из возможных пар собственных значений {a, b}, то ${\displaystyle {\hat {A}}}$ и ${\displaystyle {\hat {B}}}$ как говорят, образуют полный набор коммутирующих наблюдаемых. Однако, если уникальный набор собственных векторов по-прежнему не может быть указан, по крайней мере для одной из пар собственных значений, третья наблюдаемая ${\displaystyle {\hat {C}}}$, который работает как с ${\displaystyle {\hat {A}}}$ и ${\displaystyle {\hat {B}}}$ можно найти так, что эти три образуют полный набор коммутирующих наблюдаемых.

Отсюда следует, что собственные функции гамильтониана квантовой системы с общим значением энергии должны быть помечены путем предоставления некоторой дополнительной информации, что может быть сделано путем выбора оператора, который коммутирует с гамильтонианом. Эти дополнительные обозначения требовали наименования уникальной собственной энергетической функции и обычно связаны с константами движения системы.

Вырожденные собственные состояния энергии и оператор четности

Оператор четности определяется своим действием в ${\displaystyle |r\rangle }$ представление изменения r на -r, т.е.

${\displaystyle \langle r|P|\psi \rangle =\psi (-r)}$

Можно показать, что собственные значения P ограничиваются ${\displaystyle \pm 1}$, которые являются вырожденными собственными значениями в бесконечномерном пространстве состояний. Собственный вектор матрицы P с собственным значением +1 называется четным, а вектор с собственным значением −1 - нечетным.

Теперь четный оператор ${\displaystyle {\hat {A}}}$ тот, который удовлетворяет,

${\displaystyle {\tilde {A}}=P{\hat {A}}P}$

${\displaystyle [P,{\hat {A}}]=0}$

в то время как странный оператор ${\displaystyle {\hat {B}}}$ тот, который удовлетворяет

${\displaystyle P{\hat {B}}+{\hat {B}}P=0}$

Поскольку квадрат оператора импульса ${\displaystyle {\hat {P}}^{2}}$ четно, если потенциал V (r) четный, гамильтониан ${\displaystyle {\hat {H}}}$ называется четным оператором. В этом случае, если каждое из его собственных значений невырождено, каждый собственный вектор обязательно является собственным состоянием P, и поэтому можно искать собственные состояния ${\displaystyle {\hat {H}}}$ среди четных и нечетных состояний. Однако, если одно из собственных состояний энергии не имеет определенного паритет, можно утверждать, что соответствующее собственное значение вырождено, и ${\displaystyle P|\psi \rangle }$ является собственным вектором ${\displaystyle {\hat {H}}}$ с тем же собственным значением, что и ${\displaystyle |\psi \rangle }$.

Вырождение и симметрия

Физическая причина вырождения в квантово-механической системе часто заключается в наличии некоторых симметрия в системе. Изучение симметрии квантовой системы в некоторых случаях может позволить нам найти уровни энергии и вырождения, не решая уравнения Шредингера, что снижает усилия.

Математически связь вырождения с симметрией можно пояснить следующим образом. Рассмотрим операция симметрии связанный с унитарный оператор S. При такой операции новый гамильтониан связан с исходным гамильтонианом соотношением преобразование подобия генерируется оператором S, так что ${\displaystyle H'=SHS^{-1}=SHS^{\dagger }}$, поскольку S унитарен. Если гамильтониан остается неизменным при операции преобразования S, у нас есть

${\displaystyle SHS^{\dagger }=H}$

${\displaystyle SHS^{-1}=H}$

${\displaystyle HS=SH}$

${\displaystyle [S,H]=0}$

Сейчас если ${\displaystyle |\alpha \rangle }$ - собственное состояние энергии,

${\displaystyle H|\alpha \rangle =E|\alpha \rangle }$

где E - соответствующее собственное значение энергии.

${\displaystyle HS|\alpha \rangle =SH|\alpha \rangle =SE|\alpha \rangle =ES|\alpha \rangle }$

что обозначает ${\displaystyle S|\alpha \rangle }$ также является собственным состоянием энергии с тем же собственным значением E. Если два государства ${\displaystyle |\alpha \rangle }$ и ${\displaystyle S|\alpha \rangle }$ линейно независимы (то есть физически различны), поэтому они вырождены.

В случаях, когда S характеризуется непрерывным параметр ${\displaystyle \epsilon }$, все состояния вида ${\displaystyle S(\epsilon )|\alpha \rangle }$ имеют одинаковое собственное значение энергии.

Группа симметрии гамильтониана

Говорят, что совокупность всех операторов, коммутирующих с гамильтонианом квантовой системы, образует группа симметрии гамильтониана. В коммутаторы из генераторы этой группы определяют алгебра группы. N-мерное представление группы симметрии сохраняет Таблица умножения операторов симметрии. Возможные вырождения гамильтониана с определенной группой симметрии задаются размерностями неприводимые представления группы. Собственные функции, соответствующие n-кратно вырожденному собственному значению, образуют базис для n-мерного неприводимого представления группы симметрии гамильтониана.

Типы вырождения

Вырождения в квантовой системе могут иметь систематический или случайный характер.

Систематическое или существенное вырождение

Это также называется геометрическим или нормальным вырождением и возникает из-за наличия некоторого вида симметрии в рассматриваемой системе, то есть инвариантности гамильтониана относительно определенной операции, как описано выше. Представление, полученное из нормального вырождения, неприводимо, и соответствующие собственные функции составляют основу этого представления.

Случайное вырождение

Это тип вырождения, возникающий в результате некоторых особенностей системы или функциональной формы рассматриваемого потенциала, и, возможно, связан со скрытой динамической симметрией в системе.^[4] Это также приводит к сохранению количеств, которые часто нелегко идентифицировать. Случайные симметрии приводят к этим дополнительным вырождениям в дискретном энергетическом спектре. Случайное вырождение может быть связано с неполной группой гамильтониана. Эти вырождения связаны с существованием связанных орбит в классической физике.

Примеры: кулоновские потенциалы и потенциалы гармонического осциллятора.

Для частицы в центральной 1/р потенциал, Вектор Лапласа – Рунге – Ленца. является сохраняющейся величиной, возникающей из-за случайного вырождения, в дополнение к сохранению угловой момент из-за вращательной инвариантности.

Для частицы, движущейся по конусу под действием 1/р и р² потенциалов, центрированных на вершине конуса, сохраняющиеся величины, соответствующие случайной симметрии, будут двумя компонентами эквивалента вектора Рунге-Ленца в дополнение к одной компоненте вектора углового момента. Эти количества создают SU (2) симметрия для обоих потенциалов.

Пример: частица в постоянном магнитном поле.

Частица, движущаяся под действием постоянного магнитного поля, испытывая циклотрон движение по круговой орбите - еще один важный пример случайной симметрии. Симметрия мультиплеты в этом случае Уровни Ландау которые бесконечно вырождены.

Примеры

Атом водорода

Основная статья: Атом водорода

В атомная физика, связанные состояния электрона в атом водорода покажите нам полезные примеры вырождения. В этом случае гамильтониан коммутирует с полным орбитальный угловой момент ${\displaystyle {\hat {L^{2}}}}$, его составляющая в направлении z, ${\displaystyle {\hat {L_{z}}}}$, общий спиновый угловой момент ${\displaystyle {\hat {S^{2}}}}$ и его z-компонента ${\displaystyle {\hat {S_{z}}}}$. Квантовые числа, соответствующие этим операторам, равны ${\displaystyle l}$, ${\displaystyle m_{l}}$, ${\displaystyle s}$ (всегда 1/2 для электрона) и ${\displaystyle m_{s}}$ соответственно.

Уровни энергии в атоме водорода зависят только от главное квантовое число п. Для данного п, все состояния, соответствующие ${\displaystyle l=0,\ldots ,n-1}$ имеют одинаковую энергию и являются вырожденными. Аналогично для заданных значений п и л, то ${\displaystyle (2l+1)}$, государства с ${\displaystyle m_{l}=-l,\ldots ,l}$ вырождены. Степень вырождения уровня энергии E_п следовательно является :${\displaystyle \sum _{l\mathop {=} 0}^{n-1}(2l+1)=n^{2}}$, которая удваивается с учетом спинового вырождения.^{[1]:п. 267f}

Вырождение по ${\displaystyle m_{l}}$ является существенным вырождением, которое присутствует для любого центральный потенциал, и возникает из-за отсутствия выделенного пространственного направления. Вырождение по ${\displaystyle l}$ часто описывается как случайное вырождение, но его можно объяснить в терминах особых симметрий уравнения Шредингера, которые справедливы только для атома водорода, в котором потенциальная энергия определяется выражением Закон Кулона.^{[1]:п. 267f}

Изотропный трехмерный гармонический осциллятор

Это бесспиновый частица массы m движется в трехмерное пространство при условии центральная сила абсолютное значение которого пропорционально расстоянию частицы от центра силы.

${\displaystyle F=-kr}$

Он называется изотропным, поскольку потенциал ${\displaystyle V(r)}$ действующий на него, инвариантен относительно вращения, то есть:${\displaystyle V(r)=1/2(m\omega ^{2}r^{2})}$

куда ${\displaystyle \omega }$ это угловая частота данный ${\displaystyle {\sqrt {k/m}}}$.

Поскольку пространство состояний такой частицы есть тензорное произведение пространств состояний, связанных с отдельными одномерными волновыми функциями, не зависящее от времени уравнение Шредингера для такой системы имеет вид

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}+{\frac {\partial ^{2}\psi }{\partial z^{2}}}\right)+(1/2){m\omega ^{2}(x^{2}+y^{2}+z^{2})\psi }=E\psi }$

Итак, собственные значения энергии равны ${\displaystyle E_{n_{x},n_{y},n_{z}}=(n_{x}+n_{y}+n_{z}+3/2)\hbar \omega }$

или же, ${\displaystyle E_{n}=(n+3/2)\hbar \omega }$

где n - целое неотрицательное число, поэтому уровни энергии вырождены и степень вырожденности равна количеству различных множеств ${\displaystyle {n_{x},n_{y},n_{z}}}$ удовлетворение

${\displaystyle n_{x}+n_{y}+n_{z}=n}$

что равно

${\displaystyle \sum _{n_{x}=0}^{n}(n-n_{x}+1)=(n+1)(n+2)/2}$

Только основное состояние невырождено.

Устранение вырождения

Вырождение в квантово-механической системе может быть снято, если основная симметрия нарушена внешним возмущение. Это вызывает расщепление вырожденных уровней энергии. По сути, это расщепление исходных неприводимых представлений на такие представления возмущенной системы меньшей размерности.

Математически расщепление из-за приложения малого потенциала возмущения может быть вычислено с использованием не зависящего от времени вырожденного теория возмущений. Это аппроксимационная схема, которая может применяться для нахождения решения уравнения на собственные значения для гамильтониана H квантовой системы с приложенным возмущением, учитывая решение для гамильтониана H₀ для невозмущенной системы. Он включает в себя разложение собственных значений и собственных наборов гамильтониана H в ряд возмущений. Вырожденные собственные состояния с заданным собственным значением энергии образуют векторное подпространство, но не каждый базис собственных состояний этого пространства является хорошей отправной точкой для теории возмущений, потому что, как правило, рядом с ними не было бы собственных состояний возмущенной системы. Правильный выбор - тот, который диагонализирует гамильтониан возмущения в вырожденном подпространстве.

Снятие вырождения с помощью вырожденной теории возмущений первого порядка.

Рассмотрим невозмущенный гамильтониан ${\displaystyle {\hat {H_{0}}}}$ и возмущение ${\displaystyle {\hat {V}}}$, так что возмущенный гамильтониан ${\displaystyle {\hat {H}}={\hat {H_{0}}}+{\hat {V}}}$ Возмущенное собственное состояние без вырождения задается следующим образом: ${\displaystyle |\psi _{0}\rangle =|n_{0}\rangle +\sum _{k\neq 0}V_{k0}/(E_{0}-E_{k})|n_{k}\rangle }$ Собственный набор возмущенной энергии, а также сдвиги энергии более высокого порядка расходятся, когда ${\displaystyle E_{0}=E_{k}}$, т.е. при наличии вырождения по энергетическим уровням. Предполагая ${\displaystyle {\hat {H_{0}}}}$ обладает N вырожденными собственными состояниями ${\displaystyle |m\rangle }$ с тем же собственным значением энергии E, а также, вообще говоря, с некоторыми невырожденными собственными состояниями. Возмущенное собственное состояние ${\displaystyle |\psi _{j}\rangle }$ можно записать в виде линейного разложения по невозмущенным вырожденным собственным состояниям как ${\displaystyle |\psi _{j}\rangle =\sum _{i}|m_{i}\rangle \langle m_{i}|\psi _{j}\rangle =\sum _{i}c_{ji}|m_{i}\rangle }$ ${\displaystyle [{\hat {H_{0}}}+{\hat {V}}]\psi _{j}\rangle =[{\hat {H_{0}}}+{\hat {V}}]\sum _{i}c_{ji}|m_{i}\rangle =E_{j}\sum _{i}c_{ji}|m_{i}\rangle }$ куда ${\displaystyle E_{j}}$ относятся к собственным значениям возмущенной энергии. С ${\displaystyle E}$ является вырожденным собственным значением оператора ${\displaystyle {\hat {H_{0}}}}$, ${\displaystyle \sum _{i}c_{ji}{\hat {V}}|m_{i}\rangle =(E_{j}-E)\sum _{i}c_{ji}|m_{i}\rangle =\Delta E_{j}\sum _{i}c_{ji}|m_{i}\rangle }$ Умножение на другой невозмущенный вырожденный собственный набор ${\displaystyle \langle m_{k}|}$ дает- ${\displaystyle \sum _{i}c_{ji}[\langle m_{k}|{\hat {V}}|m_{i}\rangle -\delta _{ik}(E_{j}-E)]=0}$ Это проблема собственных значений, и запись ${\displaystyle V_{ik}=\langle m_{i}|{\hat {V}}|m_{k}\rangle }$, у нас есть- ${\displaystyle {\begin{vmatrix}V_{11}-\Delta E_{j}&V_{12}&\dots &V_{1N}\\V_{21}&V_{22}-\Delta E_{j}&\dots &V_{2N}\\\vdots &\vdots &\ddots &\vdots \\V_{N1}&V_{N2}&\dots &V_{NN}-\Delta E_{j}\end{vmatrix}}.\,}$ N собственных значений, полученных в результате решения этого уравнения, дают сдвиги на вырожденном уровне энергии из-за приложенного возмущения, в то время как собственные векторы дают возмущенные состояния в невозмущенном вырожденном базисе ${\displaystyle |m\rangle }$. Чтобы выбрать хорошие собственные состояния с самого начала, полезно найти оператор ${\displaystyle {\hat {V}}}$ который коммутирует с исходным гамильтонианом ${\displaystyle {\hat {H_{0}}}}$ и имеет одновременные собственные состояния с ним.

Физические примеры снятия вырождения возмущением

Ниже приведены некоторые важные примеры физических ситуаций, когда вырожденные энергетические уровни квантовой системы расщепляются приложением внешнего возмущения.

Нарушение симметрии в двухуровневых системах

Смотрите также: Избегаемый переход § В двух государственных системах

А двухуровневая система по существу относится к физической системе, имеющей два состояния, энергии которых близки друг к другу и сильно отличаются от энергий других состояний системы. Все расчеты для такой системы выполняются на двумерном подпространство государственного пространства.

Если основное состояние физической системы двукратно вырождено, любая связь между двумя соответствующими состояниями снижает энергию основного состояния системы и делает ее более стабильной.

Если ${\displaystyle E_{1}}$ и ${\displaystyle E_{2}}$ - уровни энергии системы, такие что ${\displaystyle E_{1}=E_{2}=E}$, а возмущение ${\displaystyle W}$ представлена ​​в двумерном подпространстве следующей матрицей 2 × 2

${\displaystyle \mathbf {W} ={\begin{bmatrix}0&W_{12}\\W_{12}^{*}&0\end{bmatrix}}.}$

то возмущенные энергии равны

${\displaystyle E_{+}=E+|W_{12}|}$

${\displaystyle E_{-}=E-|W_{12}|}$

Примеры систем с двумя состояниями, в которых вырождение по энергетическим состояниям нарушается наличием недиагональных членов в гамильтониане, возникающих в результате внутреннего взаимодействия из-за внутреннего свойства системы, включают:

• Бензол, с двумя возможными положениями трех двойных связей между соседними Углерод атомы.
• Аммиак молекула, где атом азота может находиться выше или ниже плоскости, определяемой тремя Водород атомы.
• ЧАС⁺
  ₂ молекула, в которой электрон может быть локализован вокруг любого из двух ядер.

Расщепление тонкой структуры

Основная статья: Тонкая структура

Поправки к кулоновскому взаимодействию между электроном и протоном в атоме водорода из-за релятивистского движения и спин-орбитальная связь приводят к нарушению вырождения по энергетическим уровням для разных значений л соответствует одному главному квантовому числу п.

Гамильтониан возмущения из-за релятивистской поправки имеет вид

${\displaystyle H_{r}=-p^{4}/8m^{3}c^{2}}$

куда ${\displaystyle p}$ - оператор импульса и ${\displaystyle m}$ - масса электрона. Поправка за релятивистскую энергию первого порядка в ${\displaystyle |nlm\rangle }$ основа дается

${\displaystyle E_{r}=(-1/8m^{3}c^{2})\langle nlm|p^{4}|nlm\rangle }$

Сейчас же ${\displaystyle p^{4}=4m^{2}(H^{0}+e^{2}/r)^{2}}$

${\displaystyle {\begin{aligned}E_{r}&=(-1/2mc^{2})[E_{n}^{2}+2E_{n}e^{2}\langle 1/r\rangle +e^{4}\langle 1/r^{2}\rangle ]\\&=(-1/2)mc^{2}\alpha ^{4}[-3/(4n^{4})+1/{n^{3}(l+1/2)}]\end{aligned}}}$

куда ${\displaystyle \alpha }$ это постоянная тонкой структуры.

Спин-орбитальное взаимодействие относится к взаимодействию между собственными магнитный момент электрона с магнитным полем, испытываемым им из-за относительного движения с протоном. Гамильтониан взаимодействия равен

${\displaystyle H_{so}=-(e/mc){{\vec {m}}\cdot {\vec {L}}/r^{3}}=[(e^{2}/(m^{2}c^{2}r^{3})){\vec {S}}\cdot {\vec {L}}]}$

который можно записать как

${\displaystyle H_{so}=(e^{2}/(4m^{2}c^{2}r^{3}))[{\vec {J}}^{2}-{\vec {L}}^{2}-{\vec {S}}^{2}]}$

Поправка энергии первого порядка в ${\displaystyle |j,m,l,1/2\rangle }$ базис, в котором гамильтониан возмущения диагонален, имеет вид

${\displaystyle E_{so}=(\hbar ^{2}e^{2})/(4m^{2}c^{2})[j(j+1)-l(l+1)-3/4]/((a_{0})^{3}n^{3}(l(l+1/2)(l+1))]}$

куда ${\displaystyle a_{0}}$ это Радиус Бора Полный сдвиг энергии тонкой структуры определяется выражением

${\displaystyle E_{fs}=-(mc^{2}\alpha ^{4}/(2n^{3}))[1/(j+1/2)-3/4n]}$

за ${\displaystyle j=l\pm 1/2}$.

Эффект Зеемана

Основная статья: Эффект Зеемана

Расщепление энергетических уровней атома во внешнем магнитном поле из-за взаимодействия магнитный момент ${\displaystyle {\vec {m}}}$ атома с приложенным полем известен как Эффект Зеемана.

Учитывая орбитальный и спиновой угловые моменты, ${\displaystyle {\vec {L}}}$ и ${\displaystyle {\vec {S}}}$соответственно одного электрона в атоме водорода гамильтониан возмущения имеет вид

${\displaystyle {\hat {V}}=-({\vec {m_{l}}}+{\vec {m_{s}}})\cdot {\vec {B}}}$

куда ${\displaystyle m_{l}=-e{\vec {L}}/2m}$ и ${\displaystyle m_{s}=-e{\vec {S}}/m}$.Таким образом,

${\displaystyle {\hat {V}}=e({\vec {L}}+2{\vec {S}})\cdot {\vec {B}}/2m}$

Теперь, в случае эффекта Зеемана слабого поля, когда приложенное поле слабо по сравнению с внутренним полем, спин-орбитальная связь доминирует и ${\displaystyle {\vec {L}}}$ и ${\displaystyle {\vec {S}}}$ отдельно не сохраняются. В хорошие квантовые числа находятся п, л, j и м_j, и в этом базисе поправка к энергии первого порядка может быть показана как

${\displaystyle E_{z}=-\mu _{B}g_{j}Bm_{j}}$, куда

${\displaystyle \mu _{B}={e\hbar }/2m}$ называется Бора Магнетон Таким образом, в зависимости от стоимости ${\displaystyle m_{j}}$, каждый вырожденный уровень энергии распадается на несколько уровней.

Снятие вырождения внешним магнитным полем

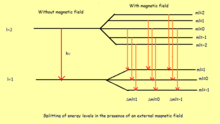
В случае эффекта Зеемана в сильном поле, когда приложенное поле достаточно велико, так что орбитальный и спиновой угловые моменты разделяются, хорошие квантовые числа теперь равны п, л, м_л, и м_s. Здесь, L_z и S_z сохраняются, поэтому гамильтониан возмущения определяется как

${\displaystyle {\hat {V}}=eB(L_{z}+2S_{z})/2m}$

считая магнитное поле вдоль z-направление. Так,

${\displaystyle {\hat {V}}=eB(m_{l}+2m_{s})/2m}$

Для каждого значения м_л, возможны два значения м_s, ${\displaystyle \pm 1/2}$.

Эффект Старка

Основная статья: Эффект Старка

Расщепление энергетических уровней атома или молекулы под действием внешнего электрического поля известно как Эффект Старка.

Для атома водорода гамильтониан возмущения имеет вид

${\displaystyle {\hat {H}}_{s}=-|e|Ez}$

если электрическое поле выбрать вдоль z-направление.

Поправки к энергии из-за приложенного поля даются математическим ожиданием ${\displaystyle {\hat {H}}_{s}}$ в ${\displaystyle |nlm\rangle }$ основание. Правила отбора показывают, что ${\displaystyle \langle nlm_{l}|z|n_{1}l_{1}m_{l1}\rangle \neq 0}$ когда ${\displaystyle l=l_{1}\pm 1}$ и ${\displaystyle m_{l}=m_{l1}}$.

Вырождение снимается только для определенных состояний, подчиняющихся правилам отбора, в первом порядке. Расщепление первого порядка по уровням энергии для вырожденных состояний ${\displaystyle |2,0,0\rangle }$ и ${\displaystyle |2,1,0\rangle }$, оба соответствуют п = 2, определяется выражением ${\displaystyle \Delta E_{2,1,m_{l}}=\pm |e|(\hbar ^{2})/(m_{e}e^{2})E}$.

Смотрите также

• Плотность состояний

Рекомендации

1. Мерцбахер, Ойген (1998). Квантовая механика (3-е изд.). Нью-Йорк: Джон Вили. ISBN  0471887021.
2. Левин, Ира Н. (1991). Квантовая химия (4-е изд.). Прентис Холл. п. 52. ISBN  0-205-12770-3.
3. Мессия, Альберт (1967). Квантовая механика (3-е изд.). Амстердам, НЛД: Северная Голландия. С. 98–106. ISBN  0471887021.
4. Макинтош, Гарольд В. (1959). «О случайном вырождении в классической и квантовой механике» (PDF). Американский журнал физики. Американская ассоциация учителей физики (AAPT). 27 (9): 620–625. Дои:10.1119/1.1934944. ISSN  0002-9505.

дальнейшее чтение

• Коэн-Таннуджи, Клод; Диу, Бернар и Лалоэ, Франк. Квантовая механика. 1. Германн. ISBN  9782705683924.^{[требуется полная цитата ]}
• Шанкар, Рамамурти (2013). Принципы квантовой механики. Springer. ISBN  9781461576754.^{[требуется полная цитата ]}
• Ларсон, Рон; Фалво, Дэвид К. (30 марта 2009 г.). Элементарная линейная алгебра, расширенное издание. Cengage Learning. С. 8–. ISBN  978-1-305-17240-1.
• Хобсон; Райли. Математические методы для физики и инженерии (Clpe) 2Ed. Издательство Кембриджского университета. ISBN  978-0-521-61296-8.
• Хеммер (2005). Kvantemekanikk: P.C. Хеммер. Тапир академиск форлаг. Tillegg 3: supplement to sections 3.1, 3.3, and 3.5. ISBN  978-82-519-2028-5.
• Quantum degeneracy in two dimensional systems, Debnarayan Jana, Dept. of Physics, University College of Science and Technology
• Al-Hashimi, Munir (2008). Accidental Symmetry in Quantum Physics.