Фазовый кубит - Phase qubit

В квантовые вычисления, а точнее в сверхпроводящие квантовые вычисления, то фазовый кубит это сверхпроводящий устройство на основе сверхпроводник – изолятор – сверхпроводник (SIS) Джозефсоновский переход,^[1] предназначен для работы в качестве квантовый бит, или кубит.^[2]

Фазовый кубит тесно связан, но отличается от кубита. поток кубита и зарядить кубит, которые также являются квантовыми битами, реализованными сверхпроводящими устройствами. Основное различие между ними - соотношение Энергия Джозефсона против зарядка энергии^[3] (необходимая энергия для одного Купер пара к обвинять общая емкость в цепи):

• Для фазового кубита это отношение порядка 10⁶, который учитывает макроскопический ток смещения через переход;
• Для потокового кубита он порядка 10, что позволяет мезоскопический сверхтоки (обычно ~ 300 нА^[4]);
• Для зарядового кубита он меньше единицы, и поэтому только несколько куперовских пар могут туннелировать и заряжать коробку с куперовскими парами. Однако, трансмон может иметь очень низкую энергию заряда из-за огромной шунтирующей емкости и, следовательно, иметь это отношение порядка 10 ~ 100.^[5]

Вступление

Фазовый кубит - это смещенный по току джозефсоновский переход, работающий в состоянии нулевого напряжения с ненулевым током смещения.

Переход Джозефсона - это туннельный переход,^[6] изготовлен из двух кусков сверхпроводящего металла, разделенных очень тонкой изолирующей перегородкой толщиной около 1 нм. Барьер достаточно тонкий, чтобы электроны или в сверхпроводящем состоянии электроны, спаренные по Куперу, могли туннелировать через барьер с заметной скоростью. Каждый из сверхпроводников, составляющих джозефсоновский переход, описывается макроскопическим волновая функция, как описано Теория Гинзбурга – Ландау для сверхпроводников.^[7] Разница в сложных фазах двух сверхпроводящих волновых функций является наиболее важной динамической переменной для джозефсоновского перехода и называется разностью фаз. ${displaystyle delta }$, или просто «фаза».

Основные уравнения, описывающие SIS-переход

В Уравнение джозефсона^[1] связывает сверхпроводящий ток (обычно называемый сверхтоком) ${displaystyle I}$ через туннельный переход к разности фаз ${displaystyle delta }$,

${displaystyle I=I_{0}sin delta }$ (Соотношение тока и фазы Джозефсона)

Здесь ${displaystyle I_{0}}$ - критический ток туннельного перехода, определяемый площадью и толщиной туннельного барьера в переходе, а также свойствами сверхпроводников по обе стороны от барьера. Для перехода с одинаковыми сверхпроводниками по обе стороны от барьера критический ток связан со сверхпроводящей щелью ${displaystyle Delta }$ и сопротивление нормального состояния ${displaystyle R_{n}}$ туннельного перехода по формуле Амбегаокара – Баратова ^[6]

${displaystyle I_{0}={frac {pi Delta }{2eR_{n}}}}$ (Формула Амбегаокара – Баратова)

Уравнение эволюции фазы Горькова.^[1] дает скорость изменения фазы ("скорость" фазы) как линейную функцию от напряжения ${displaystyle V}$ так как

${displaystyle V={frac {hbar }{2e}}{frac {ddelta }{dt}}}$ (Уравнение фазовой эволюции Горькова-Джозефсона)

Это уравнение является обобщением Уравнение Шредингера для фазы Волновая функция BCS. Обобщение было проведено Горьковым в 1958 г.^[8]

Модель Маккамбера – Стюарта

Соотношения Джозефсона переменного и постоянного тока управляют поведением самого перехода Джозефсона. Геометрия джозефсоновского перехода - двух пластин из сверхпроводящего металла, разделенных тонким туннельным барьером - аналогична геометрии конденсатора с параллельными пластинами, поэтому в дополнение к джозефсоновскому элементу устройство включает параллельную емкость ${displaystyle C}$. Внешняя цепь обычно просто моделируется как резистор. ${displaystyle R}$ параллельно с джозефсоновским элементом. Набор из трех параллельных элементов схемы запитывается внешним источником тока. ${displaystyle I}$, таким образом, смещенный по току джозефсоновский переход.^[9] Решение уравнений цепи дает одно динамическое уравнение для фазы:

${displaystyle {frac {hbar C}{2e}},{frac {d^{2}delta }{dt^{2}}}+{frac {hbar }{2eR}}{frac {ddelta }{dt}}=I-I_{0}sin delta }$.

Члены в левой части идентичны членам с координатой (местоположением) ${displaystyle delta }$, с массой, пропорциональной емкости ${displaystyle C}$, а трение обратно пропорционально сопротивлению ${displaystyle R}$. Частица движется в консервативном силовом поле, задаваемом членом справа, который соответствует частице, взаимодействующей с потенциальной энергией ${displaystyle U(delta )}$ данный

${displaystyle U(delta )={frac {hbar }{2e}}left(-I_{0}cos delta -I,delta ight)}$.

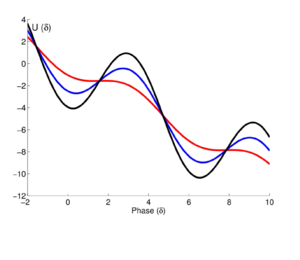
Это «потенциал стиральной доски»,^[9] так называемый, потому что он имеет общую линейную зависимость ${displaystyle -I,delta }$, модулируемый модуляцией стиральной доски ${displaystyle -I_{0},cos delta }$.

Состояние нулевого напряжения описывает одно из двух различных динамических режимов, отображаемых фазовой частицей, и соответствует тому, когда частица оказывается захваченной в одном из локальных минимумов потенциала стиральной доски. Эти минимумы существуют для токов смещения ${displaystyle left|Iight|<I_{0}}$, т.е. для токов ниже критического. Когда фазовая частица захвачена минимумом, она имеет нулевую среднюю скорость и, следовательно, нулевое среднее напряжение. Переход Джозефсона допускает токи до ${displaystyle I_{0}}$ проходить без напряжения; это соответствует сверхпроводящей ветви джозефсоновского перехода вольт-амперная характеристика.

Состояние напряжения - это другое динамическое поведение, отображаемое джозефсоновским переходом, и оно соответствует фазовой частице, свободно бегущей вниз по наклону потенциала, с ненулевой средней скоростью и, следовательно, ненулевым напряжением. Такое поведение всегда имеет место для токов ${displaystyle I}$ ток выше критического, т.е. при ${displaystyle left|Iight|>I_{0}}$, а для больших сопротивлений ${displaystyle R}$ также происходит при токах несколько ниже критического. Это состояние соответствует вольт-амперной ветви вольт-амперной характеристики джозефсоновского перехода. Для больших резистивных переходов ветви нулевого напряжения и напряжения перекрываются для некоторого диапазона токов ниже критического, поэтому поведение устройства гистерезисный.

Нелинейный индуктор

Другой способ понять поведение джозефсоновского перехода в состоянии нулевого напряжения - рассмотреть туннельный переход SIS как нелинейный индуктор.^[10] Когда фаза находится в ловушке одного из минимумов, значение фазы ограничивается небольшим диапазоном относительно значения фазы в минимуме потенциала, который мы будем называть ${displaystyle delta _{0}}$. Ток через переход связан с этим значением фазы соотношением

${displaystyle I=I_{0}sin delta _{0}}$.

Если рассматривать небольшие вариации ${displaystyle Delta delta }$ в фазе о минимуме ${displaystyle delta _{0}}$ (достаточно маленький, чтобы поддерживать переход в состоянии нулевого напряжения), тогда ток будет изменяться на

${displaystyle Delta I=left(I_{0}cos delta _{0}ight)Delta delta }$.

Эти изменения фазы приводят к возникновению напряжения через переменный ток. Отношение Джозефсона,

${displaystyle Delta V={frac {hbar }{2e}}{frac {dDelta delta }{dt}}={frac {hbar }{2e}}{frac {1}{I_{0}cos delta _{0}}}{frac {dDelta I}{dt}}=L{frac {dDelta I}{dt}}}$

Это последнее соотношение является определяющим уравнением для индуктора с индуктивностью

${displaystyle L={frac {hbar }{2e}}{frac {1}{I_{0}cos delta _{0}}}}$.

Эта индуктивность зависит от значения фазы ${displaystyle delta _{0}}$ минимум потенциала стиральной доски, поэтому значение индуктивности можно контролировать, изменяя ток смещения ${displaystyle I}$. При нулевом токе смещения индуктивность достигает минимального значения,

${displaystyle L_{m {min}}={frac {hbar }{2e}}{frac {1}{I_{0}}}={frac {hbar R_{n}}{pi Delta }}}$.

По мере увеличения тока смещения увеличивается индуктивность. Когда ток смещения очень близок (но меньше) критического тока ${displaystyle I_{0}}$, значение фазы ${displaystyle delta _{0}}$ очень близко к ${displaystyle pi /2}$, как видно из постоянного тока Отношение Джозефсона, над. Это означает, что значение индуктивности ${displaystyle L}$ становится очень большим, расходясь при ${displaystyle I}$ достигает критического тока ${displaystyle I_{0}}$.

Нелинейная катушка индуктивности представляет собой реакцию джозефсоновского перехода на изменения тока смещения. Когда параллельно индуктивности учтена параллельная емкость из геометрии устройства, это образует нелинейную ${displaystyle LC}$ резонатор, с резонансной частотой

${displaystyle omega _{p}={frac {1}{sqrt {LC}}}={sqrt {frac {2eI_{0}cos delta _{0}}{hbar C}}}}$,

которая известна как плазменная частота перехода. Это соответствует частоте колебаний фазовой частицы в нижней части одного из минимумов потенциала стиральной доски.

Для токов смещения, очень близких к критическому, значение фазы в стиральной доске минимум составляет

${displaystyle cos delta _{0}={sqrt {1-(I/I_{0})^{2}}}}$,

а плазменная частота тогда

${displaystyle omega _{p}approx {sqrt {frac {2eI_{0}}{hbar C}}}left[1-(I/I_{0})^{2}ight]^{1/4}}$,

ясно показывая, что плазменная частота приближается к нулю, когда ток смещения приближается к критическому.

Простая настройка токового смещения джозефсоновского перехода в состоянии нулевого напряжения является одним из ключевых преимуществ фазового кубита по сравнению с некоторыми другими реализациями кубита, хотя это также ограничивает производительность этого устройства, поскольку колебания тока вызывают флуктуации в плазме. частота, которая вызывает дефазировку квантовых состояний.

Квантованные уровни энергии

Фазовый кубит работает в состоянии нулевого напряжения, с ${displaystyle left|Iight|<I_{0}}$. При очень низких температурах, намного ниже 1 К (достижимо с помощью криогенной системы, известной как холодильник для разбавления ), с достаточно большим сопротивлением и малой емкостью джозефсоновского перехода, квантовые уровни энергии ^[11] становятся обнаруживаемыми в локальных минимумах потенциала стиральной доски. Впервые они были обнаружены с помощью микроволновая спектроскопия, где слабый СВЧ-сигнал добавляется к текущему ${displaystyle I}$ смещение стыка. Переходы из состояния нулевого напряжения в состояние напряжения измерялись путем отслеживания напряжения на переходе. Наблюдались четкие резонансы на определенных частотах, которые хорошо соответствовали квантовый переход энергии, полученные путем решения Уравнение Шредингера ^[12] для локального минимума потенциала стиральной доски. Обычно ожидается только один резонанс с центром на плазменной частоте. ${displaystyle omega _{p}}$. Квантово-механически, минимум потенциала в потенциале стиральной доски может вместить несколько квантованных уровней энергии, с самым низким переходом (от основного состояния к первому возбужденному) при энергии ${displaystyle E_{01}approx hbar omega _{p}}$, но переходы с более высокой энергией (из первого во второе возбужденное состояние, из второго в третье возбужденное состояние) смещены несколько ниже этого значения из-за негармонической природы минимума потенциала захвата, резонансная частота которого падает с увеличением энергии в минимум. Наблюдение нескольких дискретных уровней таким образом является чрезвычайно убедительным доказательством того, что сверхпроводящее устройство ведет себя квантово-механически, а не классически.

Фазовый кубит использует два самых низких уровня энергии в локальном минимуме; основное состояние ${displaystyle |gangle }$ является «нулевым состоянием» кубита, а первое возбужденное состояние ${displaystyle |eangle }$ это «единое государство». Наклон потенциала стиральной доски задается током смещения ${displaystyle I}$, и изменения этого тока изменяют потенциал стиральной доски, изменяя форму локального минимума (что эквивалентно изменению значения нелинейной индуктивности, как обсуждалось выше). Это изменяет разность энергий между основным и первым возбужденным состояниями. Следовательно, фазовый кубит имеет настраиваемое энергетическое расщепление.

Рекомендации

1. Бароне, Антонио; Патерно, Джанфранко (1981). Физика и приложения эффекта Джозефсона.. Нью-Йорк: Вили.
2. Нильсен, Майкл; Чуанг, Исаак (2000). Квантовые вычисления и квантовая информация. Кембридж: Издательство Кембриджского университета.
3. Вы, J. Q .; Нори, Франко (12 января 2007 г.). «Сверхпроводящие схемы и квантовая информация». Физика сегодня. 58 (11): 42. arXiv:Quant-ph / 0601121. Дои:10.1063/1.2155757. ISSN  0031-9228.
4. Делфтский университет - Веб-сайт Flux Qubit В архиве 2008-03-01 в Archive.today
5. Schreier, J. A .; Houck, A. A .; Кох, Йенс; Schuster, D. I .; Johnson, B.R .; Chow, J.M .; Gambetta, J.M .; Majer, J .; Frunzio, L .; Devoret, M. H .; Гирвин, С. М. (2008-05-12). «Подавление декогеренции зарядового шума в сверхпроводящих зарядовых кубитах». Физический обзор B. 77 (18): 180502. arXiv:0712.3581. Дои:10.1103 / PhysRevB.77.180502.
6. ван Дузер, Теодор; Тернер, Чарльз (1999). Принципы сверхпроводящих устройств и схем, 2-е изд.. Верхняя река Седл, штат Нью-Джерси: Прентис-Холл.
7. Тинкхэм, Майкл; Патерно, Джанфранко (1996). Введение в сверхпроводимость. Нью-Йорк: Макгроу-Хилл.
8. Л. П. Горьков (1958). «Об энергетическом спектре сверхпроводников». Сов. Phys. ЖЭТФ. 7 (3): 505.
9. Лихарев, Константин (1986). Динамика джозефсоновских переходов и цепей.. Нью-Йорк: Гордон и Брич.
10. Деворе, Мишель; Мартинис, Джон (2004). «Сверхпроводящие кубиты». В Эстеве, Даниэль; Raimond, J.-M .; Далибард Дж. (Ред.). Квантовая запутанность и обработка информации. Эльзевир. ISBN  0-444-51728-6.
11. Дж. М. Мартинис; М. Деворет; Дж. Кларк (1985). «Квантование уровней энергии в состоянии нулевого напряжения джозефсоновского перехода с токовым смещением» (PDF). Phys. Rev. Lett. 55 (15): 1543–1546. Bibcode:1985ПхРвЛ..55.1543М. Дои:10.1103 / PhysRevLett.55.1543. PMID  10031852.
12. Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику, 2-е изд.. Нью-Йорк: Бенджамин Каммингс. ISBN  0-13-111892-7.