Сверхпроводящие квантовые вычисления - Superconducting quantum computing - Wikipedia

Сверхпроводящие квантовые вычисления это реализация квантовый компьютер в сверхпроводящий электронные схемы. Исследования в области сверхпроводящих квантовых вычислений проводятся Google,^[1] IBM,^[2] IMEC,^[3] BBN Technologies,^[4] Ригетти,^[5] и Intel.^[6] по состоянию на май 2016 г.^{[Обновить]}, до девяти полностью управляемых кубиты демонстрируются в одномерном массиве,^[7] до шестнадцати в 2D-архитектуре.^[2]

Более двух тысяч сверхпроводящих кубитов находятся в коммерческом продукте от Системы D-Wave, однако эти кубиты реализуют квантовый отжиг вместо универсальной модели квантовых вычислений.

Устройство, состоящее из четырех сверхпроводящих трансмон кубиты, четыре квантовые автобусы, и четыре отсчета резонаторы изготовлено IBM и опубликовано в npj Квантовая информация в январе 2017 года.^[8]

Фон

Классический вычисление модели основаны на физических реализациях в соответствии с законами классическая механика.^[9] Однако известно, что классическое описание является точным только для конкретных систем с большим количеством атомов, в то время как более общее описание природы дает квантовая механика. Квантовые вычисления изучает применение квантовых явлений, выходящих за рамки классического приближения, для обработки информации и коммуникации. Существуют различные модели квантовых вычислений, однако самые популярные модели включают концепции кубиты и квантовые ворота. Кубит - это обобщение кусочек - система с двумя возможными состояниями, которые могут находиться в квантовая суперпозиция обоих. Квантовый вентиль - это обобщение логический вентиль: он описывает преобразование, которое один или несколько кубитов испытают после того, как к ним будет применен вентиль, учитывая их начальное состояние. Физическая реализация кубитов и вентилей затруднена по тем же причинам, по которым квантовые явления трудно наблюдать в повседневной жизни. Один из подходов состоит в том, чтобы реализовать квантовые компьютеры в сверхпроводниках, где квантовые эффекты становятся макроскопическими, хотя и по цене чрезвычайно низкой эксплуатации. температуры.

В сверхпроводнике основными носителями заряда являются пары электроны (известный как Куперовские пары ), а не отдельные электроны в нормальном проводнике. Общая вращение куперовской пары является целым числом, поэтому куперовские пары бозоны (в то время как одиночные электроны в нормальном проводнике фермионы ). Охлажденным бозонам, в отличие от охлажденных фермионов, позволяется занимать один квантовый энергетический уровень, что дает эффект, известный как Конденсат Бозе-Эйнштейна. В классической интерпретации это соответствовало бы множественным частицам, занимающим одно и то же положение в пространстве и имеющим равный импульс, эффективно ведя себя как одна частица.

В каждой точке сверхпроводящей электронной схемы (то есть сети электрические элементы ) конденсат волновая функция описание зарядового потока четко определяется конкретным комплексом амплитуда вероятности. В электрической цепи с нормальным проводником такое же квантовое описание справедливо для отдельных носителей заряда, однако различные волновые функции усредняются в макроскопическом анализе, что делает невозможным наблюдение квантовых эффектов. Конденсатная волновая функция позволяет проектировать и измерять макроскопические квантовые эффекты. Например, только дискретное количество кванты магнитного потока проникает в сверхпроводящую петлю, аналогично дискретному атомному уровни энергии в Модель Бора. В обоих случаях квантование является результатом комплексной амплитуды непрерывность. В отличие от микроскопических квантовых систем (таких как атомы или же фотоны ), используемых для реализации квантовых компьютеров, параметры сверхпроводящих цепей могут быть спроектированы путем установки (классических) значений электрических элементов, составляющих их, например корректировка емкость или же индуктивность.

Чтобы получить квантово-механическое описание электрической цепи, требуется несколько шагов. Во-первых, все электрические элементы описываются амплитудой и фазой конденсатной волновой функции, а не тесно связанными макроскопическими Текущий и Напряжение описание, используемое для классических схем. Например, квадрат амплитуды волновой функции в некоторой точке пространства - это вероятность найти там носитель заряда, следовательно, квадрат амплитуды соответствует классическому распределению заряда. Во-вторых, обобщенный Законы цепи Кирхгофа применяются в каждом узле схемной сети для получения уравнения движения. Наконец, уравнения движения переформулируются так: Лагранжева механика и квантовый гамильтониан выводится.

Технологии

Устройства обычно проектируются в радиочастотный спектр, остывший в холодильники разбавления ниже 100 мК и адресуется с помощью обычных электронных приборов, например синтезаторы частот и анализаторы спектра. Типичные размеры в микрометрах с субмикрометрическим разрешением позволяют удобно проектировать квантовый гамильтониан с хорошо зарекомендовавшими себя Интегральная схема технологии.

Отличительной особенностью сверхпроводящих квантовых схем является использование Джозефсоновский переход - ан электрический элемент не существует в нормальные проводники. Переход - это слабое соединение между двумя выводами сверхпроводящего провода, обычно реализуемое в виде тонкого слоя изолятора с теневое испарение техника. Конденсатные волновые функции на двух сторонах перехода слабо коррелированы - они могут иметь разные сверхпроводящие фазы, в отличие от случая сплошного сверхпроводящего провода, где сверхпроводящая волновая функция должна быть непрерывный. Ток через переход возникает по квантовое туннелирование. Это используется для создания нелинейной индуктивности, которая важна для конструкции кубита, поскольку она позволяет проектировать ангармонические осцилляторы. А квантовый гармонический осциллятор не может использоваться в качестве кубита, так как невозможно адресовать только два его состояния.

Кубит архетипы

Три архетипа сверхпроводящих кубитов - это фаза, обвинять и поток кубиты, хотя существует множество гибридизаций (Fluxonium,^[10] Трансмон,^[11] Xmon,^[12] Квантрониум^[13]). Для любой реализации кубита логический квантовые состояния ${\displaystyle \{|0\rangle ,|1\rangle \}}$ должны отображаться в различные состояния физической системы, как правило, в дискретные (квантованные) уровни энергии или их квантовые суперпозиции. В зарядовом кубите разные уровни энергии соответствуют целому числу Куперовские пары на сверхпроводящем острове. В потоковом кубите уровни энергии соответствуют разным целым числам кванты магнитного потока заключенный в сверхпроводящее кольцо. В фазовом кубите уровни энергии соответствуют разным амплитудам квантовых колебаний заряда через джозефсоновский переход, где заряд и фаза аналогичны импульсу и положению соответственно квантовый гармонический осциллятор. Обратите внимание, что фаза здесь является комплексным аргументом сверхпроводящей волновой функции, также известной как сверхпроводящий параметр порядка, а не фазой между различными состояниями кубита.

В приведенной ниже таблице рассматриваются три архетипа. В первой строке представлена ​​электрическая схема кубита. Во втором показан квантовый гамильтониан, полученный из схемы. В общем случае гамильтониан можно разделить на «кинетическую» и «потенциальную» части по аналогии с частицей в потенциальная яма. Масса частицы соответствует некоторой обратной функции емкости цепи, в то время как форма потенциала определяется регулярным индукторы и джозефсоновские переходы. Одна из первых задач в конструкции кубита - сформировать потенциальную яму и выбрать массу частицы таким образом, чтобы разделение энергии между двумя конкретными уровнями энергии отличалось от всех других разделений энергии между уровнями в системе. Эти два уровня будут использоваться как логические состояния кубита. Схематические волновые решения в третьей строке таблицы отображают комплексную амплитуду фазовой переменной. Другими словами, если фаза кубита измеряется, когда кубит находится в определенном состоянии, существует ненулевая вероятность измерить конкретное значение только там, где изображенная волновая функция колеблется. По сути, все три ряда представляют собой три разных представления одной и той же физической системы.

Архетипы сверхпроводящих кубитов^[14]

Тип Аспект	Зарядить кубит	RF-SQUID Qubit (прототип Flux Qubit)	Фаза Кубит
Схема	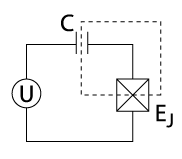Схема зарядки кубита Сверхпроводящий остров (обведен пунктирной линией), образованный между выводами конденсатор с емкость ${\displaystyle C}$ и Джозефсоновский переход с энергией ${\displaystyle E_{J}}$ предвзято из-за Напряжение ${\displaystyle U}$	Схема потокового кубита Сверхпроводящая петля с индуктивность ${\displaystyle L}$ прерывается соединение с энергией Джозефсона ${\displaystyle E_{J}}$. Предвзятость поток ${\displaystyle \Phi }$ индуцируется магнитной линией с Текущий ${\displaystyle I_{0}}$	Схема фазового кубита. Джозефсоновский переход с энергетическим параметром ${\displaystyle E_{J}}$ предвзято Текущий ${\displaystyle I_{0}}$
Гамильтониан	${\displaystyle H=E_{C}(N-N_{g})^{2}-E_{J}\cos \phi }$,куда ${\displaystyle N}$ это количество Куперовские пары к туннель то соединение, ${\displaystyle N_{g}=CV_{0}/2e}$ заряд на конденсатор в единицах количества куперовских пар, ${\displaystyle E_{C}=(2e)^{2}/2(C_{J}+C)}$ энергия заряда, связанная с емкость ${\displaystyle C}$ а емкость джозефсоновского перехода ${\displaystyle C_{J}}$, и ${\displaystyle \phi }$ это сверхпроводящий волновая функция разность фаз на переходе.	${\displaystyle H={\frac {q^{2}}{2C_{J}}}+\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]}$,куда ${\displaystyle q}$ заряд на соединение емкость ${\displaystyle C_{J}}$ и ${\displaystyle \phi }$ это сверхпроводящий волновая функция разность фаз на переходе Джозефсона. ${\displaystyle \phi }$ разрешено принимать значения больше, чем ${\displaystyle 2\pi }$, и, таким образом, альтернативно определяется как интеграл по времени от Напряжение вдоль индуктивность ${\displaystyle L}$.	${\displaystyle H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi }$, куда ${\displaystyle C_{J}}$ это емкость связанный с Джозефсоновский переход, ${\displaystyle \Phi _{0}}$ это квант магнитного потока, ${\displaystyle q}$ это заряд на емкости перехода ${\displaystyle C_{J}}$ и ${\displaystyle \phi }$ - фаза на стыке.
Потенциал	Зарядный кубитный потенциал Потенциальная часть гамильтониана, ${\displaystyle -E_{J}\cos \phi }$, обозначен толстой красной линией. Схема волновая функция решения изображены тонкими линиями, приподнятыми до нужного уровень энергии для ясности. Для вычислений используются только сплошные волновые функции. Предвзятость Напряжение установлен так, что ${\displaystyle N_{g}={\frac {1}{2}}}$, сводя к минимуму энергетический разрыв между ${\displaystyle |0\rangle }$ и ${\displaystyle |1\rangle }$, тем самым делая зазор отличным от других энергетических зазоров (например, зазор между ${\displaystyle |1\rangle }$ и ${\displaystyle |2\rangle }$). Разница в промежутках позволяет адресовать переходы из ${\displaystyle |0\rangle }$ к ${\displaystyle |1\rangle }$ и только наоборот, без заполнения других состояний, таким образом эффективно обрабатывая схему как двухуровневую систему (кубит ).	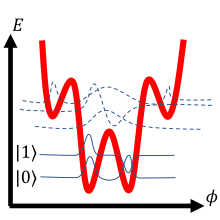Потенциал потока кубита Потенциальная часть гамильтониана, ${\displaystyle \left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]}$, построенный для смещения поток ${\displaystyle \Phi =\Phi _{0}/2}$, обозначен толстой красной линией. Схема волновая функция решения изображаются тонкими линиями, приподнятыми до соответствующих уровень энергии для ясности. Для вычислений используются только сплошные волновые функции. Разные колодцы соответствуют разному количеству кванты потока в ловушке сверхпроводящих петель. Два нижних состояния соответствуют симметричному и антисимметричному суперпозиция нулевых или одиночных захваченных квантов потока, иногда обозначаемых как состояния контура по часовой стрелке и против часовой стрелки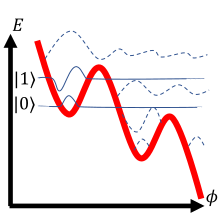: ${\displaystyle |0\rangle =\left[|\circlearrowleft \rangle +|\circlearrowright \rangle \right]/{\sqrt {2}}}$ и ${\displaystyle |1\rangle =\left[|\circlearrowleft \rangle -|\circlearrowright \rangle \right]/{\sqrt {2}}}$.	Фазовый кубитный потенциал Так называемая "стиральная доска" потенциальная часть гамильтониана, ${\displaystyle -I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi }$, обозначен толстой красной линией. Схема волновая функция решения изображаются тонкими линиями, приподнятыми до нужного уровень энергии для ясности. Для вычислений используются только сплошные волновые функции. Предвзятость Текущий настроен таким образом, чтобы скважины были достаточно мелкими, чтобы содержать ровно две локализованные волновые функции. Небольшое увеличение тока смещения вызывает селективный «разлив» более высокого энергетического состояния (${\displaystyle |1\rangle }$), выраженная с помощью измеримого Напряжение спайк - механизм, обычно используемый для фазового кубита измерение.

Отдельные кубиты

Энергетический зазор в ГГц между уровнями энергии сверхпроводящего кубита специально разработан для обеспечения совместимости с доступным электронным оборудованием из-за терагерцовый промежуток - отсутствие оборудования в верхнем диапазоне частот. В дополнение запрещенная зона сверхпроводника подразумевает верхний предел работы ниже ~ 1 ТГц (за его пределами пары Купера ломаются). С другой стороны, разделение уровней энергии не может быть слишком маленьким из-за соображений охлаждения: температура 1K означает колебания энергии 20 ГГц. Температуры в десятки милли-Кельвина, достигаемые в холодильниках с разбавлением, позволяют кубиту работать при разделении уровней энергии ~ 5 ГГц. Разделение уровней энергии кубита часто можно регулировать посредством управления выделенной линией тока смещения, предоставляя «ручку» для точной настройки параметров кубита.

Однокубитовые вентили

Произвольный однокубитный вентиль достигается вращением в Сфера Блоха. Вращения между различными уровнями энергии одного кубита вызваны микроволновая печь импульсы, отправленные на антенну или линия передачи связан с кубитом с частотой, резонансной с разделением по энергии между уровнями. Отдельные кубиты могут быть адресованы выделенным линия передачи, или общим, если остальные кубиты не в резонансе. Ось вращения устанавливается квадратурная амплитудная модуляция СВЧ-импульса, а длина импульса определяет угол поворота.^[15]

Более формально, следуя обозначениям,^[15] для управляющего сигнала

${\displaystyle {\mathcal {E}}(t)={\mathcal {E}}^{x}(t)\cos(\omega _{d}t)+{\mathcal {E}}^{y}(t)\sin(\omega _{d}t)}$

частоты ${\displaystyle \omega _{d}}$, гамильтониан управляемого кубита в приближение вращающейся волны является

${\displaystyle H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}}$,

куда ${\displaystyle \omega }$ - резонанс кубита и ${\displaystyle \sigma _{x},\sigma _{y}}$ находятся Матрицы Паули.

Чтобы реализовать вращение вокруг ${\displaystyle X}$ ось, можно установить ${\displaystyle {\mathcal {E}}^{y}(t)=0}$ и подать микроволновый импульс с частотой ${\displaystyle \omega _{d}=\omega }$ На время ${\displaystyle t_{g}}$. Результирующее преобразование

${\displaystyle U_{x}=\exp \left\{-{\frac {i}{\hbar }}\int _{0}^{t_{g}}H^{R}dt\right\}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}}$,

это именно то оператор вращения ${\displaystyle R_{X}(\theta )}$ по углу ${\displaystyle \theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt}$ о ${\displaystyle X}$ ось в сфере Блоха. Произвольный поворот вокруг ${\displaystyle Y}$ ось может быть реализована аналогичным образом. Отображения двух операторов вращения достаточно для универсальности, поскольку каждый отдельный кубитный унитарный оператор ${\displaystyle U}$ может быть представлен как ${\displaystyle U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})}$ (до глобального фаза, что физически неважно) с помощью процедуры, известной как ${\displaystyle X-Y}$ разложение.^[16]

Например, установка ${\displaystyle \int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi }$ результаты с преобразованием

${\displaystyle U_{x}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}=e^{-i\pi \sigma _{x}/2}=-i\sigma _{x}}$,

это известно как НЕ ворота (до глобальной фазы ${\displaystyle -i}$).

Связывание кубитов

Связывание кубитов необходимо для реализации 2-кубитных вентилей. Связь двух кубитов может быть достигнута путем подключения их к промежуточной электрической цепи связи. Схема может быть фиксированным элементом, например, конденсатор, или управляемый, например DC-SQUID. В первом случае разъединение кубитов (в то время, когда вентиль выключен) достигается за счет настройки кубитов из резонанса друг от друга, то есть деления энергетических зазоров между их вычислительными состояниями разными.^[17] Этот подход по своей сути ограничен возможностью связи только ближайших соседей, поскольку между подключенными кубитами должна быть проложена физическая электрическая цепь. В частности, Системы D-Wave Связь ближайших соседей обеспечивает высокосвязную элементарную ячейку из 8 кубитов в конфигурации графа Химеры. Как правило, квантовые алгоритмы требуют связи между произвольными кубитами, поэтому ограничение связности, вероятно, потребует нескольких замена операции, ограничивающие длину возможного квантового вычисления до декогеренции процессора.

Другой метод соединения двух или более кубитов - соединение их с промежуточной квантовой шиной. Квантовая шина часто реализуется как микроволновая печь, смоделированный квантовый гармонический осциллятор. Связанные кубиты могут входить и выходить из резонанса с шиной и друг с другом, что устраняет ограничение ближайшего соседа. Формализм, используемый для описания этой связи: квантовая электродинамика резонатора, где кубиты аналогичны атомам, взаимодействующим с оптическим фотонным резонатором, с разницей в ГГц, а не в ТГц режиме электромагнитного излучения.

Поперечный резонансный гейт

Один популярный стробирующий механизм включает в себя два кубита и шину, настроенных на разное разделение уровней энергии. Применение микроволнового возбуждения к первому кубиту с частотой, резонансной со вторым кубитом, вызывает ${\displaystyle \sigma _{x}}$ вращение второго кубита. Направление вращения зависит от состояния первого кубита, что позволяет управляемый фазовый вентиль строительство.^[18]

Более формально, следуя обозначениям,^[18] гамильтониан возбуждения, описывающий систему, возбуждаемую первой линией движения кубита, имеет вид

${\displaystyle H_{D}/\hbar =A(t)\cos({\tilde {\omega }}_{2}t)\left(\sigma _{x}\otimes I-{\frac {J}{\Delta _{12}}}\sigma _{z}\otimes \sigma _{x}+m_{12}I\otimes \sigma _{x}\right)}$,

куда ${\displaystyle A(t)}$ - форма микроволнового импульса во времени, ${\displaystyle {\tilde {\omega }}_{2}}$ - резонансная частота второго кубита, ${\displaystyle \{I,\sigma _{x},\sigma _{y},\sigma _{z}\}}$ являются Матрицы Паули, ${\displaystyle J}$ - коэффициент связи между двумя кубитами через резонатор, ${\displaystyle \Delta _{12}\equiv \omega _{1}-\omega _{2}}$ - расстройка кубита, ${\displaystyle m_{12}}$ это случайная (нежелательная) связь между кубитами и ${\displaystyle \hbar }$ является Постоянная Планка деленное на ${\displaystyle 2\pi }$. Интеграл по времени по ${\displaystyle A(t)}$ определяет угол поворота. Нежелательные повороты из-за первого и третьего членов гамильтониана можно компенсировать с помощью операций с одним кубитом. Оставшаяся часть в сочетании с одиночными поворотами кубита составляет основу алгебры Ли su (4).

Считывание кубита

Считывание для конкретной архитектуры (измерение ) механизмы существуют. Считывание фазового кубита объясняется в таблица архетипов кубитов над. Состояние потокового кубита часто считывается настраиваемым магнитометром DC-SQUID. Более общая схема считывания включает связь с микроволновым резонатором, где резонансная частота резонатора смещается на состояние кубита.^[19]

Критерии Ди Винченцо

Список Критерии Ди Винченцо для физической системы для реализации логического кубита удовлетворяет сверхпроводящая реализация. Проблемы, с которыми в настоящее время сталкивается сверхпроводящий подход, в основном относятся к области микроволновой техники.^[19]

1. Масштабируемая физическая система с хорошо изученными кубитами. Поскольку сверхпроводящие кубиты изготавливаются на кристалле, многокубитовая система легко масштабируется с кубитами, размещенными на двумерной поверхности кристалла. Большая часть текущих усилий по разработке заключается в достижении взаимосвязи, управления и считывания в третьем измерении с дополнительными слоями литографии. Потребность в хорошо охарактеризованных кубитах удовлетворяется с помощью (а) кубитной нелинейности, доступ к только двум из доступных уровней энергии и (б) доступа к одному кубиту за раз, а не ко всей многокубитной системе, по каждому кубиту. выделенные линии управления и / или частотное разделение (настройка) различных кубитов.
2. Возможность инициализировать состояние кубитов до простого реперного состояния. Один из простых способов инициализировать кубит - подождать достаточно долго, пока кубит не успокоится до своего основного энергетического состояния. Кроме того, управление потенциалом кубита с помощью ручки настройки позволяет ускорить механизмы инициализации.
3. Длительное время релевантной декогеренции. На декогеренцию сверхпроводящих кубитов влияет несколько факторов. В основном это связано с качеством джозефсоновского перехода и несовершенствами подложки чипа. Из-за своего мезоскопического масштаба сверхпроводящие кубиты относительно недолговечны. Тем не менее тысячи операций вентилей были продемонстрированы в многокубитных системах.^[20]
4. «Универсальный» набор квантовых вентилей. Сверхпроводящие кубиты позволяют произвольно вращать сферу Блоха с помощью импульсных микроволновых сигналов, тем самым реализуя произвольные одиночные кубитные вентили. ${\displaystyle \sigma _{z}\sigma _{z}}$ и ${\displaystyle \sigma _{x}\sigma _{x}}$ муфты показаны для большинства реализаций, дополняя универсальный набор вентилей.^[21][22]
5. Возможность измерения, зависящего от кубита. В общем, к одному сверхпроводящему кубиту можно обращаться для контроля или измерения.

внешняя ссылка

• IBM Quantum Experience позволяет строить и запускать квантовые алгоритмы на процессоре с 16 сверхпроводящими кубитами.
• В Сеть IBM Q предлагает доступ к коммерческим 20-кубитным системам и протестировал 50-кубитный прототип, который будет доступен в сети в следующем поколении.

Рекомендации

1. Кастельвекки, Давиде (5 января 2017 г.). «Квантовые компьютеры готовы выпрыгнуть из лаборатории в 2017 году». Природа. С. 9–10. Bibcode:2017Натура.541 .... 9С. Дои:10.1038 / 541009a.
2. «IBM делает квантовые вычисления доступными в IBM Cloud». www-03.ibm.com. 4 мая 2016.
3. «Imec вступает в гонку, чтобы развязать квантовые вычисления с кремниевыми кубитами». www.imec-int.com. Получено 2019-11-10.
4. Колм А. Райан, Блейк Р. Джонсон, Диего Ристе, Брайан Донован, Томас А. Оки, «Аппаратное обеспечение для динамических квантовых вычислений», arXiv: 1704.08314v1
5. «Rigetti запускает квантовые облачные сервисы и объявляет о вызове на 1 миллион долларов». HPCwire. 2018-09-07. Получено 2018-09-16.
6. «Intel инвестирует 50 миллионов долларов в развитие квантовых вычислений | Intel Newsroom». Отдел новостей Intel.
7. Келли, Дж .; Barends, R .; Fowler, A. G .; Megrant, A .; Джеффри, Э .; White, T. C .; Санк, Д .; Mutus, J. Y .; Кэмпбелл, B .; Чен, Ю; Chen, Z .; Chiaro, B .; Dunsworth, A .; Hoi, I.-C .; Neill, C .; О’Мэлли, П. Дж. Дж .; Кинтана, С .; Roushan, P .; Вайнсенчер, А .; Wenner, J .; Cleland, A.N .; Мартинис, Джон М. (4 марта 2015 г.). «Сохранение состояния путем обнаружения повторяющихся ошибок в сверхпроводящей квантовой схеме». Природа. 519 (7541): 66–69. arXiv:1411.7403. Bibcode:2015Натура.519 ... 66K. Дои:10.1038 / природа14270. PMID  25739628.
8. Gambetta, J.M .; Чоу, Дж. М.; Штеффен, М. (2017). «Построение логических кубитов в сверхпроводящей квантовой вычислительной системе». npj Квантовая информация. 3 (1): 2. Bibcode:2017npjQI ... 3 .... 2G. Дои:10.1038 / с41534-016-0004-0.
9. Дайал, Гита. «Машина Тьюринга LEGO проста, но возвышена». ПРОВОДНОЙ.
10. Манучарян, В. Э .; Koch, J .; Глазман, Л. И .; Деворет, М. Х. (1 октября 2009 г.). «Флюксоний: схема с одиночной медной парой без смещений заряда». Наука. 326 (5949): 113–116. arXiv:0906.0831. Bibcode:2009Наука ... 326..113М. Дои:10.1126 / science.1175552. PMID  19797655.
11. Houck, A. A .; Кох, Йенс; Devoret, M. H .; Гирвин, С. М .; Шелькопф, Р. Дж. (11 февраля 2009 г.). «Жизнь после шума заряда: последние результаты с трансмонными кубитами». Квантовая обработка информации. 8 (2–3): 105–115. arXiv:0812.1865. Дои:10.1007 / s11128-009-0100-6.
12. Barends, R .; Келли, Дж .; Megrant, A .; Санк, Д .; Джеффри, Э .; Chen, Y .; Инь, Й .; Chiaro, B .; Mutus, J .; Neill, C .; O’Malley, P .; Roushan, P .; Wenner, J .; White, T. C .; Cleland, A.N .; Мартинис, Джон М. (22 августа 2013 г.). «Когерентный кубит Джозефсона, подходящий для масштабируемых квантовых интегральных схем». Письма с физическими проверками. 111 (8): 080502. arXiv:1304.2322. Bibcode:2013ПхРвЛ.111х0502Б. Дои:10.1103 / PhysRevLett.111.080502. PMID  24010421.
13. Metcalfe, M .; Боакнин, Э .; Манучарян, В .; Vijay, R .; Сиддики, I .; Rigetti, C .; Frunzio, L .; Schoelkopf, R.J .; Деворет, М. Х. (21 ноября 2007 г.). «Измерение декогеренции квантрониевого кубита с бифуркационным усилителем резонатора». Физический обзор B. 76 (17): 174516. arXiv:0706.0765. Bibcode:2007PhRvB..76q4516M. Дои:10.1103 / PhysRevB.76.174516.
14. Devoret, M. H .; Wallraff, A .; Мартинис, Дж. М. (6 ноября 2004 г.). «Сверхпроводящие кубиты: краткий обзор». arXiv:cond-mat / 0411174.
15. Motzoi, F .; Gambetta, J.M .; Rebentrost, P .; Вильгельм, Ф. К. (8 сентября 2009 г.). «Простые импульсы для устранения утечки в слабо нелинейных кубитах». Письма с физическими проверками. 103 (11): 110501. arXiv:0901.0534. Bibcode:2009ПхРвЛ.103к0501М. Дои:10.1103 / PhysRevLett.103.110501. PMID  19792356.
16. Чуанг, Майкл А. Нильсен и Исаак Л. (2010). Квантовые вычисления и квантовая информация (10-летие изд.). Кембридж: Издательство Кембриджского университета. стр.174 –176. ISBN  978-1-107-00217-3.
17. Ригетти, Чад Тайлер (2009). Квантовые ворота для сверхпроводящих кубитов. п. 21. Bibcode:2009ПХДТ ........ 50Р. ISBN  9781109198874.
18. Чоу, Джерри М .; Córcoles, A.D .; Гамбетта, Джей М .; Ригетти, Чад; Johnson, B.R .; Смолин, Джон А .; Rozen, J. R .; Киф, Джордж А .; Ротвелл, Мэри Б.; Кетчен, Марк Б .; Штеффен, М. (17 августа 2011 г.). «Простой запутывающий вентиль, работающий только в микроволновом диапазоне, для сверхпроводящих кубитов фиксированной частоты». Письма с физическими проверками. 107 (8): 080502. arXiv:1106.0553. Bibcode:2011ПхРвЛ.107х0502С. Дои:10.1103 / PhysRevLett.107.080502. PMID  21929152.
19. Гамбетта, Джей М .; Чоу, Джерри М .; Штеффен, Маттиас (13 января 2017 г.). «Создание логических кубитов в сверхпроводящей квантовой вычислительной системе». npj Квантовая информация. 3 (1): 2. Bibcode:2017npjQI ... 3 .... 2G. Дои:10.1038 / с41534-016-0004-0.
20. Devoret, M. H .; Шелькопф, Р. Дж. (7 марта 2013 г.). "Сверхпроводящие схемы для квантовой информации: обзор". Наука. 339 (6124): 1169–1174. Bibcode:2013Научный ... 339.1169D. Дои:10.1126 / science.1231930. PMID  23471399.
21. Чоу, Джерри М .; Гамбетта, Джей М .; Córcoles, A.D .; Меркель, Сет Т .; Смолин, Джон А .; Ригетти, Чад; Poletto, S .; Киф, Джордж А .; Ротуэлл, Мэри Б.; Rozen, J. R .; Кетчен, Марк Б .; Штеффен, М. (9 августа 2012 г.). «Универсальный квантовый вентиль, приближающийся к порогам отказоустойчивости с помощью сверхпроводящих кубитов». Письма с физическими проверками. 109 (6): 060501. arXiv:1202.5344. Bibcode:2012PhRvL.109f0501C. Дои:10.1103 / PhysRevLett.109.060501. PMID  23006254.
22. Niskanen, A. O .; Harrabi, K .; Yoshihara, F .; Nakamura, Y .; Lloyd, S .; Цай, Дж. С. (4 мая 2007 г.). «Квантовая когерентная перестраиваемая связь сверхпроводящих кубитов». Наука. 316 (5825): 723–726. Bibcode:2007Научный ... 316..723N. Дои:10.1126 / science.1141324. PMID  17478714.