Симметричная убывающая перестановка - Symmetric decreasing rearrangement

В математика, то симметричная убывающая перестановка функции - это симметричная убывающая функция, наборы уровней имеют тот же размер, что и исходная функция.^[1]

Определение множеств

Учитывая измеримый набор, ${\displaystyle A}$, в р^п , определяется симметричная перестановка из ${\displaystyle A}$, называется ${\displaystyle A^{*}}$, как шар с центром в начале координат, объем которого (Мера Лебега ) такая же, как и у множества ${\displaystyle A}$.

Эквивалентное определение:

${\displaystyle A^{*}=\{x\in \mathbf {R} ^{n}:\,\omega _{n}\cdot |x|^{n}<|A|\},}$

куда ${\displaystyle \omega _{n}}$ объем единичный мяч и где ${\displaystyle |A|}$ объем ${\displaystyle A}$.

Определение функций

Перестановка неотрицательной измеримой действительной функции ${\displaystyle f}$ чей уровень устанавливает ${\displaystyle f^{-1}(y)}$ (${\displaystyle y\in \mathbb {R} _{\geq 0}}$) имеют конечную меру

${\displaystyle f^{*}(x)=\int _{0}^{\infty }\mathbb {I} _{\{y:f(y)>t\}^{*}}(x)\,dt,}$

куда ${\displaystyle \mathbb {I} _{A}}$ обозначает индикаторная функция из набора А. На словах ценность ${\displaystyle f^{*}(x)}$ дает высоту ${\displaystyle t}$ для которого радиус симметричной перестановки ${\displaystyle \{y:f(y)>t\}}$ равно ${\displaystyle x}$. У нас есть следующая мотивация для этого определения. Потому что личность

${\displaystyle g(x)=\int _{0}^{\infty }\mathbb {I} _{\{y:g(y)>t\}}(x)\,dt,}$

выполняется для любой неотрицательной функции ${\displaystyle g}$, приведенное выше определение является единственным определением, которое заставляет тождество ${\displaystyle \mathbb {I} _{A}^{*}=\mathbb {I} _{A^{*}}}$ держать.

Характеристики

Функция и ее симметричная убывающая перестановка сохраняют меру множеств уровней.

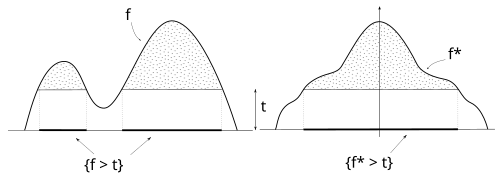
Функция ${\displaystyle f^{*}}$ - симметричная убывающая функция, множества уровней которой имеют ту же меру, что и множества уровней ${\displaystyle f}$, т.е.

${\displaystyle |\{x:f^{*}(x)>t\}|=|\{x:f(x)>t\}|.}$

Если ${\displaystyle f}$ функция в ${\displaystyle L^{p}}$, тогда

${\displaystyle \|f\|_{L^{p}}=\|f^{*}\|_{L^{p}}.}$

В Неравенство Харди – Литтлвуда выполняется, т.е.

${\displaystyle \int fg\leq \int f^{*}g^{*}.}$

Далее Неравенство Полиа – Сегё держит. Это говорит о том, что если ${\displaystyle 1\leq p<\infty }$ и если ${\displaystyle f\in W^{1,p}}$ тогда

${\displaystyle \|\nabla f^{*}\|_{p}\leq \|\nabla f\|_{p}.}$

Симметричная убывающая перестановка сохраняет порядок и уменьшает ${\displaystyle L^{p}}$ расстояние, т.е.

${\displaystyle f\leq g\Rightarrow f^{*}\leq g^{*}}$

и

${\displaystyle \|f-g\|_{L^{p}}\geq \|f^{*}-g^{*}\|_{L^{p}}.}$

Приложения

Неравенство Полиа – Сегё в предельном случае дает ${\displaystyle p=1}$, то изопериметрическое неравенство. Кроме того, можно использовать некоторые соотношения с гармоническими функциями для доказательства Неравенство Рэлея – Фабера – Крана..

Несимметричная убывающая перегруппировка

Мы также можем определить f * как функцию от неотрицательных действительных чисел, а не от всех R^п.^[2] Пусть (E, μ) - произвольная σ-пространство с конечной мерой, и разреши ${\displaystyle f:E\to [-\infty ,\infty ]}$ быть измеримая функция который принимает только конечные (т.е. реальные) значения μ-п.в. (где «μ-п.в.» означает кроме, возможно, на множестве μ-меры нуль). Мы определяем функция распределения ${\displaystyle \mu _{f}:[0,\infty ]\to [0,\infty ]}$ по правилу

${\displaystyle \mu _{f}(s)=\mu \{x\in E:f(x)>s\}.}$

Теперь мы можем определить убывающая перестановка (или, иногда, невозрастающая перестановка функции f как функции ${\displaystyle f^{*}:[0,\infty )\to [0,\infty ]}$ и правило

${\displaystyle f^{*}(t)=\inf\{s\in [0,\infty ]:\mu _{f}(s)\leq t\}.}$

Обратите внимание, что эта версия убывающей перестановки не является симметричной, так как она определена только для неотрицательных действительных чисел. Однако он наследует многие из тех же свойств, перечисленных выше, что и симметричная версия. А именно:

f и f * являются равноизмеримый, т.е. имеют одинаковую функцию распределения.

Справедливо неравенство Харди-Литтлвуда, т. Е. ${\displaystyle \int _{E}|fg|\;d\mu \leq \int _{0}^{\infty }f^{*}(t)g^{*}(t)\;dt.}$

${\displaystyle f\leq g}$ μ-п.в. подразумевает ${\displaystyle f^{*}\leq g^{*}}$.

${\displaystyle (af)^{*}=|a|f^{*}}$ для всех действительных чисел a.

${\displaystyle (f+g)^{*}(t_{1}+t_{2})\leq f^{*}(t_{1})+g^{*}(t_{2})}$ для всех ${\displaystyle t_{1},t_{2}\in [0,\infty )}$.

${\displaystyle |f_{n}|\uparrow |f|}$ μ-п.в. подразумевает ${\displaystyle f_{n}^{*}\uparrow f^{*}}$.

${\displaystyle (f^{p})^{*}=(f^{*})^{p}}$ для всех положительных действительных чисел p.

${\displaystyle \|f\|_{L_{p}(E)}=\|f^{*}\|_{L_{p}[0,\infty )}}$ для всех положительных действительных чисел p.

${\displaystyle \|f\|_{L_{\infty }(E)}=f^{*}(0).}$

(Несимметричная) убывающая функция перестановки часто возникает в теории перестановочно-инвариантных банаховых функциональных пространств. Особенно важно следующее:

Теорема Люксембург о представлении. Позволять ${\displaystyle \rho }$ - перестановочно-инвариантная норма банаховой функции над резонансным пространством с мерой ${\displaystyle (E,\mu )}$. Тогда существует (возможно, не единственная) перестановочно-инвариантная функциональная норма ${\displaystyle {\overline {\rho }}}$ на ${\displaystyle [0,\infty )}$ такой, что ${\displaystyle \rho (f)={\overline {\rho }}(f^{*})}$ для всех неотрицательных измеримых функций ${\displaystyle f:E\to [0,\infty ]}$ которые являются конечнозначными μ-п. в.

Обратите внимание, что определения всей терминологии в приведенной выше теореме (т. Е. Норм банаховых функций, перестановочно-инвариантных банаховых функциональных пространств и пространств с резонансной мерой) можно найти в разделах 1 и 2 книги Беннета и Шарпли (см. Ссылки ниже ).

Смотрите также

• Изопериметрическое неравенство
• Представление слоеного торта
• Неравенство Рэлея – Фабера – Крана.
• Неравенство перестановки Рисса
• Соболевское пространство
• Неравенство Сегё

Рекомендации

1. Либ, Эллиотт; Потеря, Майкл (2001). Анализ. Аспирантура по математике. 14 (2-е изд.). Американское математическое общество. ISBN  978-0821827833.
2. Беннет, Колин; Шарпли, Роберт (1988). Интерполяция операторов. ISBN  978-0-120-88730-9.