Многогранник A5 - A5 polytope
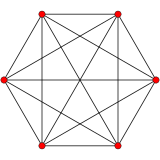 5-симплекс |
В 5-мерном геометрия, всего 19 однородные многогранники с А5 симметрия. Есть одна самодуальная регулярная форма, 5-симплекс с 6 вершинами.
Каждый может быть визуализирован как симметричный орфографические проекции в Самолеты Кокстера А5 Группа Кокстера и другие подгруппы.
Графики
Симметричный орфографические проекции из этих 19 многогранников можно составить в A5, А4, А3, А2 Самолеты Кокстера. Аk графики имеют [k + 1] симметрия. Для четных k и симметрично nodea_1ed-диаграмм симметрия удваивается до [2 (k + 1)].
Каждый из этих 19 многогранников показан в этих 4 плоскостях симметрии с нарисованными вершинами и ребрами, а вершины окрашены числом перекрывающихся вершин в каждой проективной позиции.
| # | Самолет Кокстера графики | Диаграмма Кокстера-Дынкина Символ Шлефли имя | |||
|---|---|---|---|---|---|
| [6] | [5] | [4] | [3] | ||
| А5 | А4 | А3 | А2 | ||
| 1 |  |  |  |  | {3,3,3,3} 5-симплекс (hix) |
| 2 |  |  |  |  | т1{3,3,3,3} или r {3,3,3,3} Ректифицированный 5-симплексный (Рикс) |
| 3 |  |  |  |  | т2{3,3,3,3} или 2r {3,3,3,3} Биректифицированный 5-симплекс (точка) |
| 4 |  |  |  |  | т0,1{3,3,3,3} или т {3,3,3,3} Усеченный 5-симплексный (тикс) |
| 5 |  |  |  |  | т1,2{3,3,3,3} или 2т {3,3,3,3} Bitruncated 5-симплекс (биттикс) |
| 6 |  |  |  |  | т0,2{3,3,3,3} или р-р {3,3,3,3} Сквозной 5-симплексный (саркс) |
| 7 |  |  |  |  | т1,3{3,3,3,3} или 2rr {3,3,3,3} Бикантеллированный 5-симплексный (сибрид) |
| 8 |  |  |  |  | т0,3{3,3,3,3} Ранцинированный 5-симплекс (спикс) |
| 9 |  |  | 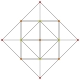 |  | т0,4{3,3,3,3} или 2r2r {3,3,3,3} Стерилизованный 5-симплексный (scad) |
| 10 |  |  |  |  | т0,1,2{3,3,3,3} или tr {3,3,3,3} Cantitruncated 5-симплекс (гаркс) |
| 11 |  |  |  |  | т1,2,3{3,3,3,3} или 2тр {3,3,3,3} Бикантитроусеченный 5-симплекс (гибрид) |
| 12 |  |  | 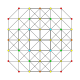 |  | т0,1,3{3,3,3,3} Runcitruncated 5-симплекс (Паттикс) |
| 13 |  |  | 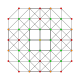 |  | т0,2,3{3,3,3,3} Runcicantellated 5-симплекс (пиркс) |
| 14 |  |  |  |  | т0,1,4{3,3,3,3} Стеритоусеченный 5-симплекс (cappix) |
| 15 |  |  |  |  | т0,2,4{3,3,3,3} Стерикантеллированный 5-симплекс (карта) |
| 16 |  |  | 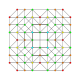 |  | т0,1,2,3{3,3,3,3} Runcicantitruncated 5-симплекс (гиппикс) |
| 17 |  |  | 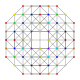 |  | т0,1,2,4{3,3,3,3} Стериканитусеченный 5-симплекс (cograx) |
| 18 |  |  |  |  | т0,1,3,4{3,3,3,3} Стерино-усеченный 5-симплексный (captid) |
| 19 |  |  |  |  | т0,1,2,3,4{3,3,3,3} Омнитусеченный 5-симплексный (gocad) |
| Многогранники A5 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 т0 |  т1 |  т2 |  т0,1 |  т0,2 |  т1,2 |  т0,3 | |||||
 т1,3 |  т0,4 |  т0,1,2 |  т0,1,3 |  т0,2,3 |  т1,2,3 |  т0,1,4 | |||||
 т0,2,4 |  т0,1,2,3 |  т0,1,2,4 |  т0,1,3,4 |  т0,1,2,3,4 | |||||||
использованная литература
- H.S.M. Coxeter:
- H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: Избранные произведения Х.С.М. Coxeterпод редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
внешние ссылки
- Клитцинг, Ричард. "5D однородные многогранники (политеры)".
