Функция активации - Activation function

О формализме, используемом для аппроксимации влияния внеклеточного электрического поля на нейроны, см. функция активации. Для передаточной функции линейной системы см. функция передачи.

Функция логистической активации

В искусственные нейронные сети, то функция активации узла определяет выход этого узла, учитывая вход или набор входов. Стандарт Интегральная схема можно рассматривать как цифровая сеть функций активации, которые могут быть «ВКЛ» (1) или «ВЫКЛ» (0), в зависимости от входа. Это похоже на поведение линейный перцептрон в нейронные сети. Однако только нелинейный Функции активации позволяют таким сетям решать нетривиальные задачи, используя лишь небольшое количество узлов, и такие функции активации называются нелинейности.^[1]

Функции

Наиболее распространенные функции активации можно разделить на три категории: коньковые функции, радиальные функции и функции складывания.

Функции активации конька

Основная статья: Ридж-функция

Ридж-функции - это одномерные функции, действующие на линейную комбинацию входных переменных. Часто используемые примеры включают:

• Линейный активация: ${\displaystyle \phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b} }$,
• ReLU активация: ${\displaystyle \phi (\mathbf {v} )=\max(0,a+\mathbf {v} '\mathbf {b} )}$,
• Хевисайд активация: ${\displaystyle \phi (\mathbf {v} )=1_{a+\mathbf {v} '\mathbf {b} >0}}$,
• Логистика активация: ${\displaystyle \phi (\mathbf {v} )=(1+\exp(-a-\mathbf {v} '\mathbf {b} ))^{-1}}$.

В биологически вдохновленные нейронные сети, функция активации обычно представляет собой абстракцию, представляющую скорость потенциал действия стрельба в камере.^[2] В простейшем виде это функция двоичный - то есть либо нейрон стреляет или нет. Функция выглядит как ${\displaystyle \phi (\mathbf {v} )=U(a+\mathbf {v} '\mathbf {b} )}$, куда ${\displaystyle U}$ это Ступенчатая функция Хевисайда.

Линия позитива склон может использоваться для отражения увеличения скорости воспламенения, которое происходит при увеличении входного тока. Такая функция будет иметь вид ${\displaystyle \phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b} }$.

Поскольку биологические нейроны не могут снизить свою скорость возбуждения ниже нуля, выпрямленный линейный Функции активации используются: ${\displaystyle \phi (\mathbf {v} )=\max(0,a+\mathbf {v} '\mathbf {b} )}$. Они вводят нелинейность в нуле, которую можно использовать для принятия решений.^[3]

Выпрямленные линейные единицы и функции активации линейных единиц погрешности по Гауссу

Нейроны также не могут стрелять быстрее определенной скорости, что мотивирует сигмовидный функции активации, область определения которых является конечным интервалом.

Радиальные функции активации

Основная статья: Радиальная функция

Особый класс функций активации, известный как радиальные базисные функции (RBF) используются в Сети RBF, которые чрезвычайно эффективны как универсальные аппроксиматоры функций. Эти функции активации могут принимать разные формы, но обычно они находятся в одной из следующих функций:

• Гауссовский: ${\displaystyle \,\phi (\mathbf {v} )=\exp \left(-{\frac {\|\mathbf {v} -\mathbf {c} \|^{2}}{2\sigma ^{2}}}\right)}$
• Мультиквадраты: ${\displaystyle \,\phi (\mathbf {v} )={\sqrt {\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}}}}$
• Обратные мультиквадраты: ${\displaystyle \,\phi (\mathbf {v} )=\left(\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}\right)^{-{\frac {1}{2}}}}$
• Полигармонические сплайны

куда ${\displaystyle \mathbf {c} }$ вектор, представляющий функцию центр и ${\displaystyle a}$ и ${\displaystyle \sigma }$ параметры, влияющие на разброс радиуса.

Была предложена эффективная с вычислительной точки зрения радиальная базисная функция,^[4] называется ядром RBF на основе квадратичного закона (SQ-RBF ), который устраняет экспоненциальный член, как в гауссовском RBF.

• SQ-RBF: ${\displaystyle f(\mathbf {v} )={\begin{cases}1-{\frac {1}{2}}\|\mathbf {v} -\mathbf {c} \|^{2}&:\|\mathbf {v} -\mathbf {c} \|\leq 1\\{\frac {1}{2}}(2-\|\mathbf {v} -\mathbf {c} \|)^{2}&:1\leq \|\mathbf {v} -\mathbf {c} \|\leq 2\\0&:\|\mathbf {v} -\mathbf {c} \|\geq 2.\end{cases}}}$

Функции активации складывания

Основная статья: Функция складывания

Функции активации складывания широко используются в слои объединения в сверточные нейронные сети, и в выходных слоях мультиклассовых сетей классификации. Эти активации выполняют агрегирование по входам, например, принимают иметь в виду, минимум или же максимум. В мультиклассовой классификации softmax активация часто используется.

Сравнение функций активации

Есть множество функций активации. В основополагающей статье 2012 года Хинтона и др. Об автоматическом распознавании речи используется логистическая функция активации сигмовидной кишки.^[5] Основополагающий 2012 год AlexNet Архитектура компьютерного зрения использует функцию активации ReLU, как и основополагающая архитектура компьютерного зрения 2015 года. ResNet. Основополагающая модель языковой обработки 2018 года БЕРТ использует гладкую версию ReLU, GELU.^[6]

Помимо эмпирической эффективности, функции активации также обладают различными математическими свойствами:

Нелинейный

Когда функция активации нелинейна, то двухслойная нейронная сеть может быть доказана как универсальный аппроксиматор функции.^[7] Это известно как Универсальная аппроксимационная теорема. Функция активации идентификации не удовлетворяет этому свойству. Когда несколько уровней используют функцию активации идентичности, вся сеть эквивалентна одноуровневой модели.

Классифицировать

Когда диапазон функции активации конечен, методы обучения на основе градиента имеют тенденцию быть более стабильными, поскольку представление паттернов существенно влияет только на ограниченные веса. Когда диапазон бесконечен, обучение, как правило, более эффективно, потому что представление паттернов значительно влияет на большинство весов. В последнем случае меньше скорость обучения обычно необходимы.^{[нужна цитата ]}

Непрерывно дифференцируемый

Это свойство желательно (ReLU не является непрерывно дифференцируемым и имеет некоторые проблемы с оптимизацией на основе градиента, но это все еще возможно) для включения методов оптимизации на основе градиента. Функция активации бинарного шага не дифференцируется на 0, и она дифференцируется до 0 для всех других значений, поэтому методы на основе градиента не могут добиться прогресса с ней.^[8]

Монотонный

Когда функция активации является монотонной, поверхность ошибки, связанная с однослойной моделью, гарантированно будет выпуклой.^[9]

Гладкие функции с монотонной производной

Было показано, что в некоторых случаях они лучше обобщают.

Приближает личность около происхождения

Когда функции активации имеют это свойство, нейронная сеть будет эффективно обучаться, когда ее веса инициализируются небольшими случайными значениями. Если функция активации не приближает идентичность к исходной точке, необходимо соблюдать особую осторожность при инициализации весов.^[10] В таблице ниже функции активации, где ${\displaystyle f(0)=0}$ и ${\displaystyle f'(0)=1}$ и ${\displaystyle f'}$ непрерывна в 0, отмечены как обладающие этим свойством.

Эти свойства не оказывают решающего влияния на производительность и не являются единственными математическими свойствами, которые могут быть полезны. Например, строго положительный диапазон softplus делает его пригодным для прогнозирования отклонений в вариационные автокодеры.

В следующей таблице сравниваются свойства нескольких функций активации, которые являются функциями одного складывать Икс из предыдущего слоя или слоев:

Имя	участок	Функция, ${\displaystyle f(x)}$	Производная из ${\displaystyle f}$, ${\displaystyle f'(x)}$	Классифицировать	Порядок преемственности	Монотонный	Монотонная производная	Приближает личность около происхождения
Личность		${\displaystyle x}$	${\displaystyle 1}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{\infty }}$	да	да	да
Двоичный шаг		${\displaystyle {\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle {\begin{cases}0&{\text{if }}x\neq 0\\{\text{undefined}}&{\text{if }}x=0\end{cases}}}$	${\displaystyle \{0,1\}}$	${\displaystyle C^{-1}}$	да	Нет	Нет
Логистика, сигмовидная или мягкая шаг		${\displaystyle \sigma (x)={\frac {1}{1+e^{-x}}}}$[1]	${\displaystyle f(x)(1-f(x))}$	${\displaystyle (0,1)}$	${\displaystyle C^{\infty }}$	да	Нет	Нет
танх		${\displaystyle \tanh(x)={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}$	${\displaystyle 1-f(x)^{2}}$	${\displaystyle (-1,1)}$	${\displaystyle C^{\infty }}$	да	Нет	да
Выпрямленный линейный блок (ReLU)[11]		${\displaystyle {\begin{aligned}&{\begin{cases}0&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}\\{}={}&\max\{0,x\}=x{\textbf {1}}_{x>0}\end{aligned}}}$	${\displaystyle {\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x>0\\{\text{undefined}}&{\text{if }}x=0\end{cases}}}$	${\displaystyle [0,\infty )}$	${\displaystyle C^{0}}$	да	да	Нет
Линейная единица погрешности по Гауссу (GELU)[6]		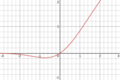${\displaystyle {\begin{aligned}&{\frac {1}{2}}x\left(1+{\text{erf}}\left({\frac {x}{\sqrt {2}}}\right)\right)\\{}={}&x\Phi (x)\end{aligned}}}$	${\displaystyle \Phi (x)+x\phi (x)}$	${\displaystyle (-0.17\ldots ,\infty )}$	${\displaystyle C^{\infty }}$	Нет	Нет	Нет
Softplus[12]		${\displaystyle \ln \left(1+e^{x}\right)}$	${\displaystyle {\frac {1}{1+e^{-x}}}}$	${\displaystyle (0,\infty )}$	${\displaystyle C^{\infty }}$	да	да	Нет
Экспоненциальная линейная единица (ELU)[13]		${\displaystyle {\begin{cases}\alpha \left(e^{x}-1\right)&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}}$ с параметром ${\displaystyle \alpha }$	${\displaystyle {\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x>0\\1&{\text{if }}x=0{\text{ and }}\alpha =1\end{cases}}}$	${\displaystyle (-\alpha ,\infty )}$	${\displaystyle {\begin{cases}C^{1}&{\text{if }}\alpha =1\\C^{0}&{\text{otherwise}}\end{cases}}}$	Iff ${\displaystyle \alpha \geq 0}$	Iff ${\displaystyle 0\leq \alpha \leq 1}$	Iff ${\displaystyle \alpha =1}$
Масштабируемая экспоненциальная линейная единица (SELU)[14]		${\displaystyle \lambda {\begin{cases}\alpha (e^{x}-1)&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}}$ с параметрами ${\displaystyle \lambda =1.0507}$ и ${\displaystyle \alpha =1.67326}$	${\displaystyle \lambda {\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle (-\lambda \alpha ,\infty )}$	${\displaystyle C^{0}}$	да	Нет	Нет
Линейный блок с выпрямителем с утечкой (Leaky ReLU)[15]		${\displaystyle {\begin{cases}0.01x&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle {\begin{cases}0.01&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0}}$	да	да	Нет
Параметрический выпрямленный линейный блок (ПРэЛУ)[16]		${\displaystyle {\begin{cases}\alpha x&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}}$ с параметром ${\displaystyle \alpha }$	${\displaystyle {\begin{cases}\alpha &{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$[2]	${\displaystyle C^{0}}$	Iff ${\displaystyle \alpha \geq 0}$	да	Iff ${\displaystyle \alpha =1}$
ElliotSig,[17][18] софтсайн[19][20]		${\displaystyle {\frac {x}{1+|x|}}}$	${\displaystyle {\frac {1}{(1+|x|)^{2}}}}$	${\displaystyle (-1,1)}$	${\displaystyle C^{1}}$	да	Нет	да
Квадратная нелинейность (SQNL)[21]		${\displaystyle {\begin{cases}1&{\text{if }}x>2.0\\x-{\frac {x^{2}}{4}}&{\text{if }}0\leq x\leq 2.0\\x+{\frac {x^{2}}{4}}&{\text{if }}-2.0\leq x<0\\-1&{\text{if }}x<-2.0\end{cases}}}$	${\displaystyle 1\mp {\frac {x}{2}}}$	${\displaystyle (-1,1)}$	${\displaystyle C^{1}}$	да	Нет	да
S-образный выпрямленный блок линейной активации (СРеЛУ)[22]		${\displaystyle {\begin{cases}t_{l}+a_{l}(x-t_{l})&{\text{if }}x\leq t_{l}\\x&{\text{if }}t_{l}<x<t_{r}\\t_{r}+a_{r}(x-t_{r})&{\text{if }}x\geq t_{r}\end{cases}}}$ куда ${\displaystyle t_{l},a_{l},t_{r},a_{r}}$ параметры.	${\displaystyle {\begin{cases}a_{l}&{\text{if }}x\leq t_{l}\\1&{\text{if }}t_{l}<x<t_{r}\\a_{r}&{\text{if }}x\geq t_{r}\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0}}$	Нет	Нет	Нет
Согнутая личность		${\displaystyle {\frac {{\sqrt {x^{2}+1}}-1}{2}}+x}$	${\displaystyle {\frac {x}{2{\sqrt {x^{2}+1}}}}+1}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{\infty }}$	да	да	да
Сигмовидная линейная единица (SiLU,[6] SiL,[23] или Swish-‍1[24])		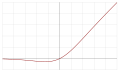${\displaystyle {\frac {x}{1+e^{-x}}}}$	${\displaystyle {\frac {1+e^{-x}+xe^{-x}}{\left(1+e^{-x}\right)^{2}}}}$	${\displaystyle [-0.278\ldots ,\infty )}$	${\displaystyle C^{\infty }}$	Нет	Нет	За ${\displaystyle 2f(x)}$
Гауссовский		${\displaystyle e^{-x^{2}}}$	${\displaystyle -2xe^{-x^{2}}}$	${\displaystyle (0,1]}$	${\displaystyle C^{\infty }}$	Нет	Нет	Нет
SQ-RBF		${\displaystyle {\begin{cases}1-{\frac {x^{2}}{2}}&{\text{if }}|x|\leq 1\\{\frac {1}{2}}(2-|x|)^{2}&{\text{if }}1<|x|<2\\0&{\text{if }}|x|\geq 2\end{cases}}}$	${\displaystyle {\begin{cases}-x&{\text{if }}|x|\leq 1\\x-2\operatorname {sgn}(x)&{\text{if }}1<|x|<2\\0&{\text{if }}|x|\geq 2\end{cases}}}$	${\displaystyle [0,1]}$	${\displaystyle C^{0}}$	Нет	Нет	Нет

^ Здесь, ${\displaystyle \sigma }$ это логистическая функция.

^ ${\displaystyle \alpha >0}$ чтобы диапазон был верным.

В следующей таблице перечислены функции активации, которые не являются функциями одного складывать Икс из предыдущего слоя или слоев:

Имя	Уравнение, ${\displaystyle f_{i}\left({\vec {x}}\right)}$	Производные, ${\displaystyle {\frac {\partial f_{i}\left({\vec {x}}\right)}{\partial x_{j}}}}$	Классифицировать	Порядок преемственности
Softmax	${\displaystyle {\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}}$ за я = 1, …, J	${\displaystyle f_{i}\left({\vec {x}}\right)\left(\delta _{ij}-f_{j}\left({\vec {x}}\right)\right)}$[3][4]	${\displaystyle (0,1)}$	${\displaystyle C^{\infty }}$
Использовать полностью[25]	${\displaystyle \max _{i}x_{i}}$	${\displaystyle {\begin{cases}1&{\text{if }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{if }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0}}$

^ Здесь, ${\displaystyle \delta _{ij}}$ это Дельта Кронекера.

^ Например, ${\displaystyle j}$ может перебирать количество ядер предыдущего слоя нейронной сети, в то время как ${\displaystyle i}$ перебирает количество ядер текущего слоя.

Смотрите также

• Логистическая функция
• Выпрямитель (нейронные сети)
• Стабильность (теория обучения)
• Функция Softmax

Рекомендации

1. Хинкельманн, Кнут. "Нейронные сети, стр. 7" (PDF). Университет прикладных наук Северо-Западной Швейцарии.
2. Ходжкин, А.Л .; Хаксли, А. Ф. (1952-08-28). «Количественное описание мембранного тока и его применение к проводимости и возбуждению в нерве». Журнал физиологии. 117 (4): 500–544. Дои:10.1113 / jphysiol.1952.sp004764. ЧВК  1392413. PMID  12991237.
3. Бенке, Свен (2003). Иерархические нейронные сети для интерпретации изображений. Конспект лекций по информатике. 2766. Springer. Дои:10.1007 / b11963. ISBN  978-3-540-40722-5. S2CID  1304548.
4. Вураола, Адедамола; Патель, Нитиш (2018), «Вычислительная эффективная радиальная базисная функция», 2018 Международная конференция по обработке нейронной информации (ICONIP), Сиемреап, Камбоджа: Springer, стр. 103–112, Дои:10.1007/978-3-030-04179-3_9
5. Хинтон, Джеффри; Дэн Ли; Дэн Ли; Ю, Донг; Даль, Джордж; Мохамед, Абдель-Рахман; Джайтли, Навдип; Старший, Андрей; Ванхаук, Винсент; Нгуен, Патрик; Саинат, Тара; Кингсбери, Брайан (2012). «Глубокие нейронные сети для акустического моделирования в распознавании речи».
6. Хендрикс, Дэн; Гимпель, Кевин (2016). «Линейные единицы с ошибкой Гаусса (GELU)». arXiv:1606.08415 [cs.LG ].
7. Цибенко, Г. (декабрь 1989 г.). «Аппроксимация суперпозициями сигмоидальной функции». Математика управления, сигналов и систем. 2 (4): 303–314. Дои:10.1007 / BF02551274. ISSN  0932-4194. S2CID  3958369.
8. Сниман, янв (3 марта 2005 г.). Практическая математическая оптимизация: введение в основную теорию оптимизации и классические и новые градиентные алгоритмы. Springer Science & Business Media. ISBN  978-0-387-24348-1.
9. У, Хуайцинь (2009). «Анализ глобальной устойчивости общего класса разрывных нейронных сетей с функциями активации линейного роста». Информационные науки. 179 (19): 3432–3441. Дои:10.1016 / j.ins.2009.06.006.
10. Сусильо, Дэвид; Эбботт, Л. Ф. (19 декабря 2014 г.). «Инициализация случайного блуждания для обучения очень глубоких сетей прямого распространения». arXiv:1412.6558 [cs.NE ].
11. Наир, Винод; Хинтон, Джеффри Э. (2010), «Выпрямленные линейные блоки улучшают машины Больцмана с ограничениями», 27-я Международная конференция Международной конференции по машинному обучению, ICML'10, США: Omnipress, стр. 807–814, ISBN  9781605589077
12. Глорот, Ксавьер; Бордес, Антуан; Бенжио, Йошуа (2011). «Нейронные сети глубокого разреженного выпрямителя» (PDF). Международная конференция по искусственному интеллекту и статистике.
13. Клеверт, Джорк-Арне; Унтертинер, Томас; Хохрайтер, Зепп (23 ноября 2015 г.). «Быстрое и точное глубокое обучение сети с помощью экспоненциальных линейных единиц (ELU)». arXiv:1511.07289 [cs.LG ].
14. Кламбауэр, Гюнтер; Унтертинер, Томас; Майр, Андреас; Хохрайтер, Зепп (2017-06-08). «Самонормализующиеся нейронные сети». Достижения в системах обработки нейронной информации. 30 (2017). arXiv:1706.02515. Bibcode:2017arXiv170602515K.
15. Maas, Andrew L .; Hannun, Awni Y .; Нг, Эндрю Ю. (июнь 2013 г.). «Нелинейность выпрямителя улучшает акустические модели нейронной сети». Proc. ICML. 30 (1). S2CID  16489696.
16. Он, Кайминг; Чжан, Сянъюй; Рен, Шаоцин; Сунь, Цзянь (06.02.2015). «Углубляясь в выпрямители: превосходя человеческий уровень производительности по классификации ImageNet». arXiv:1502.01852 [cs.CV ].
17. Эллиот, Дэвид Л. (1993), "Лучшая функция активации для искусственных нейронных сетей", Технический отчет ISR TR 93-8, Мэрилендский университет, Колледж-Парк, Мэриленд 20742., CiteSeerX  10.1.1.46.7204
18. "Эллиотсиг, симметричная сигмовидная передаточная функция Эллиота", Команда представлена ​​в Matlab R2012b, документации Matlab, MathWorks.
19. Бергстра, Джеймс; Дежарден, Гийом; Ламблин, Паскаль; Бенжио, Йошуа (2009). «Квадратичные многочлены лучше узнают особенности изображения». Технический отчет 1337 ". Département d’Informatique et de Recherche Opérationnelle, Université de Montréal. Архивировано из оригинал на 2018-09-25.
20. Глорот, Ксавьер; Бенджио, Йошуа (2010), «Понимание сложности обучения глубоких нейронных сетей с прямой связью» (PDF), Международная конференция по искусственному интеллекту и статистике (AISTATS'10), Общество искусственного интеллекта и статистики
21. Вураола, Адедамола; Патель, Нитиш (2018), «SQNL: новая эффективная в вычислительном отношении функция активации», 2018 Международная совместная конференция по нейронным сетям (IJCNN), Рио-де-Жанейро, Бразилия: IEEE, стр. 1–7.
22. Цзинь, Сяоцзе; Сюй, Чуньян; Фэн, Цзиаши; Вэй, Юньчао; Xiong, Junjun; Ян, Шуйчэн (22 декабря 2015 г.). «Глубокое обучение с S-образными выпрямленными линейными модулями активации». arXiv:1512.07030 [cs.CV ].
23. Эльфокрыл, Стефан; Учибе, Эйдзи; Дойя, Кенджи (2018). «Сигмоидно-взвешенные линейные единицы для аппроксимации функций нейронной сети в обучении с подкреплением». Нейронные сети. 107: 3–11. arXiv:1702.03118. Дои:10.1016 / j.neunet.2017.12.012. PMID  29395652. S2CID  6940861.
24. Рамачандран, Праджит; Зоф, Баррет; Ле, Куок V (2017). «Поиск функций активации». arXiv:1710.05941 [cs.NE ].
25. Гудфеллоу, Ян Дж .; Вард-Фарли, Дэвид; Мирза, Мехди; Курвиль, Аарон; Бенжио, Йошуа (2013). "Maxout Networks". Материалы семинара и конференции JMLR. 28 (3): 1319–1327. arXiv:1302.4389. Bibcode:2013arXiv1302.4389G.