Связность - Connectedness
Эта статья нужны дополнительные цитаты для проверка. (Июль 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
В математика, связность[1] используется для обозначения различных свойств, в некотором смысле означающих «все как одно целое». Когда математический объект обладает таким свойством, мы говорим, что это связаны; в противном случае это отключен. Когда разъединенный объект можно естественным образом разделить на соединенные части, каждую часть обычно называют компонент (или же связный компонент).
Связность в топологии
А топологическое пространство как говорят связаны если это не союз двух непересекающийся непустой открытые наборы.[2] А набор открыто, если в нем нет точек, лежащих на его граница; таким образом, в неформальном, интуитивном смысле, тот факт, что пространство может быть разделено на непересекающиеся открытые множества, предполагает, что граница между двумя наборами не является частью пространства, и, таким образом, разделяет его на две отдельные части.
Другие понятия связности
Области математики обычно связаны с объектами особого типа. Часто такой объект называют связаны если, если рассматривать его как топологическое пространство, это связное пространство. Таким образом, коллекторы, Группы Ли, и графики все называются связаны если они связаны как топологические пространства, а их компоненты являются топологическими компонентами. Иногда бывает удобно перефразировать определение связности в таких областях. Например, граф называется связаны если каждая пара вершины в графе соединяется дорожка. Это определение эквивалентно топологическому применительно к графам, но с ним легче работать в контексте теория графов. Теория графов также предлагает бесконтекстную меру связности, называемую коэффициент кластеризации.
Другие области математики связаны с объектами, которые редко рассматриваются как топологические пространства. Тем не менее, определения связность часто тем или иным образом отражают топологический смысл. Например, в теория категорий, а категория как говорят связаны если каждая пара объектов в нем соединена последовательностью морфизмы. Таким образом, категория связана, если интуитивно все это одно целое.
Могут быть разные представления о связность которые интуитивно похожи, но отличаются как формально определенные концепции. Мы могли бы пожелать назвать топологическим пространством связаны если каждая пара точек в нем соединена дорожка. Однако это условие оказывается сильнее стандартной топологической связности; в частности, существуют связные топологические пространства, для которых это свойство не выполняется. Из-за этого используется другая терминология; пространства с этим свойством называются путь подключен. Хотя не все связанные пространства связаны путями, все пространства, соединенные путями, связаны.
Условия, включающие связаны также используются для свойств, которые связаны со связностью, но явно отличаются от нее. Например, линейно связное топологическое пространство односвязный если каждый цикл (путь от точки к себе) в нем сжимаемый; то есть интуитивно, если существует только один способ добраться из любой точки в любую другую. Таким образом, сфера и диск односвязны, а тор не является. Другой пример: ориентированный граф является сильно связанный если каждый упорядоченная пара вершин соединяется направленный путь (то есть тот, который «следует по стрелкам»).
Другие концепции выражают способ, которым объект нет связаны. Например, топологическое пространство полностью отключен если каждый из его компонентов представляет собой одну точку.
Связь
Свойства и параметры, основанные на идее связности, часто включают слово возможность подключения. Например, в теория графов, а связный граф - это та, из которой мы должны удалить хотя бы одну вершину, чтобы создать несвязный граф.[3] В связи с этим такие графы также называют 1-связный. Точно так же граф 2-связный если мы должны удалить из него хотя бы две вершины, чтобы создать несвязный граф. А 3-связный граф требует удаления не менее трех вершин и т. д. В возможность подключения графа - это минимальное количество вершин, которое необходимо удалить, чтобы его разъединить. Эквивалентно связность графа - это наибольшее целое число k для которого график k-связаны.
Хотя терминология меняется, имя существительное формы свойств, связанных со связностью, часто включают термин возможность подключения. Таким образом, при обсуждении односвязных топологических пространств гораздо чаще говорят о простое подключение чем простая связность. С другой стороны, в полях без формально определенного понятия возможность подключения, это слово может использоваться как синоним для связность.
Другой пример связности можно найти в обычных мозаиках. Здесь возможность подключения описывает количество соседей, доступных из одного плитка:
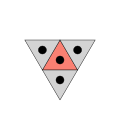
3-подключение в треугольная черепица,

6-подключение в шестиугольная черепица,

8-подключение в квадратная черепица (обратите внимание, что равенство расстояний не сохраняется)
Смотрите также
- связанное пространство
- подключенная категория
- компонент связности (теория графов)
- связанная сумма
- перекрестная ссылка
- сеть
- Безмасштабная сеть
- односвязный
- сеть малого мира
- компонент сильной связности
- полностью отключен
Рекомендации
- ^ "определение связности". Dictionary.com. Получено 2016-06-15.
- ^ Мункрес, Джеймс (2000). Топология. Пирсон. п. 148. ISBN 978-0131816299.
- ^ Bondy, J.A .; Мурти, США. (1976). Теория графов и приложения. Нью-Йорк, штат Нью-Йорк: Elsevier Science Publishing Co., стр.42. ISBN 0444194517.




