Складывание карты - Map folding - Wikipedia
в математика складывания бумаги, складывание карты и складывание штампа это две проблемы подсчета количества способов сложить лист бумаги. В задаче сгиба штампа бумага представляет собой полосу штампов со складками между ними, причем складки должны лежать на складках. В задаче складывания карты бумага представляет собой карту, разделенную складками на прямоугольники, и складки должны снова лежать только вдоль этих складок.
Лукас (1891) приписывает изобретение проблемы складывания штампа Эмиль Лемуан.[1] Тушар (1950) предоставляет несколько других ранних ссылок.[2]
Маркированные марки
В задаче складывания штампа бумага, которую нужно сложить, представляет собой полосу квадратных или прямоугольных штампов, разделенных складками, и штампы можно складывать только по этим складкам. В одной из часто рассматриваемых версий задачи каждый штамп считается отличимые друг от друга штампы, поэтому два сгиба полосы штампов считаются эквивалентными, только если они имеют одинаковую вертикальную последовательность штампов.[3]Например, есть шесть способов сложить полосу из трех разных марок:

К ним относятся все шесть перестановок марок, но для более чем трех марок возможны не все перестановки. Если для перестановки п, есть два числа я и j с тем же паритет так что четыре числа я, j, я + 1, и j + 1 появляться в п в этом циклический порядок, тогда п не складывается. Условие четности подразумевает, что складки между марками я и я + 1, и между марками j и j + 1, появляются на одной стороне стопки сложенных марок, но условие циклического упорядочения подразумевает, что эти две складки пересекаются друг с другом, что физически невозможно. Например, четырехэлементная перестановка 1324 не может быть свернута, потому что она имеет этот запрещенный образец с я = 1 и j = 3. Все оставшиеся перестановки, без этого шаблона, можно складывать.[3]Количество разных способов сложить полоску п марки дается по порядку
- 1, 2, 6, 16, 50, 144, 462, 1392, 4536, 14060, 46310, 146376, 485914, 1557892, 5202690, ... (последовательность A000136 в OEIS ).
Эти числа всегда делятся на п (потому что циклическая перестановка складываемой последовательности штампа всегда сам складывается),[3][4] и частные этого деления равны
- 1, 1, 2, 4, 10, 24, 66, 174, 504, 1406, 4210, 12198, 37378, 111278, 346846, 1053874, ... (последовательность A000682 в OEIS ),
количество топологически различных способов, которыми полубесконечная кривая может сделать п переходы с линией, называемые «полуузловыми».
| Нерешенная проблема в математике: Есть ли формула или алгоритм с полиномиальным временем для подсчета решений проблемы складывания штампа? (больше нерешенных задач по математике) |
В 1960-х годах Джон Э. Келер и У. Ф. Ланнон реализовали алгоритмы который в то время мог рассчитать эти числа для 28 марок.[5][6][7]Несмотря на дополнительные исследования, известные методы расчета этих чисел принимают экспоненциальное время как функция п.[8][9]Таким образом, не существует известной формулы или эффективного алгоритма, который мог бы расширить эту последовательность до очень больших значений п. Тем не менее, эвристический методы из физики могут быть использованы для предсказания скорости экспоненциальный рост этой последовательности.[10]
Задача сгиба штампа обычно рассматривает только количество возможных состояний сгиба полосы штампов, не учитывая, возможно ли физически построить сгиб последовательностью движений, начиная с развернутой полосы штампов. Однако согласно решению проблема правила плотника каждое свернутое состояние может быть построено (или, что эквивалентно, может быть развернуто).[11]
Немаркированные марки
В другом варианте задачи фальцовки штампа полоса штампов считается пустой, так что невозможно отличить один из ее концов от другого, и два фальца считаются разными, только если они имеют разные формы. Переворачивание сложенной полосы вверх ногами или изнаночной стороной вперед не считается изменением ее формы, поэтому три марки имеют только два сгиба, S-образную кривую и спираль.[3] В более общем смысле, количество складок с этим определением равно
- 1, 1, 2, 5, 14, 38, 120, 353, 1148, 3527, 11622, 36627, 121622, 389560, 1301140, 4215748, ... (последовательность A001011 в OEIS )
Карты
Складывание карты - это вопрос о том, сколькими способами можно сложить прямоугольную карту вдоль ее складок, чтобы каждая складка образовывала складку горы или долины. Он отличается от складывания штампа тем, что включает в себя как вертикальные, так и горизонтальные складки, а не только складки в одном направлении.[12]
Существует восемь способов сложить карту 2 × 2 вдоль ее складок, считая каждую отдельную вертикальную последовательность сложенных квадратов как отдельный способ складывания карты:[5]
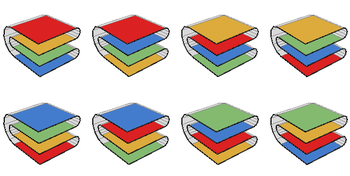
Однако общая проблема подсчета количества способов сложить карту остается нерешенной. Количество способов складывания п × п карта известна только п ≤ 7. Они есть:
Сложность
| Нерешенная проблема в математике: Учитывая назначение складок карты горной долине, можно ли эффективно проверить, можно ли ее сложить? (больше нерешенных задач по математике) |
Проблемы сгибания карты и сгиба штампа связаны с проблемой в математика оригами можно ли сложить квадрат с рисунком сгиба в плоскую фигуру. горная складка или складка долины ) присваивается каждой складке полоски штампов, можно проверить, можно ли сложить результат полиномиальное время.[13]
Для той же задачи на карте (разделенной на прямоугольники складками с заданными направлениями) неизвестно, существует ли вообще алгоритм полиномиального сворачивания по времени, хотя полиномиальный алгоритм известен для 2 × п карты.[14]В ограниченном случае, когда карта должна быть сложена последовательностью «простых» складок, которые складывают бумагу вдоль одной линии, проблема является полиномиальной. Некоторые расширения проблемы, например, на непрямоугольные листы бумаги, находятся НП-полный.[13]
Даже для одномерной полосы марок, сгибы которой уже обозначены как складки гор или долин, NP-жесткий найти способ сложить его, чтобы минимизировать максимальное количество штампов, лежащих между двумя штампами любой складки.[15]
Смотрите также
- Обычная последовательность складывания бумаги, бесконечная последовательность нулей и единиц, описывающая один способ складывания полосок штампов.
Рекомендации
- ^ Лукас, Эдуард (1891), Теория Номбр (На французском), я, Париж: Готье-Виллар, стр. 120.
- ^ Тушар, Жак (1950), "Contribution à l'étude du problème des timbres poste", Канадский математический журнал (На французском), 2: 385–398, Дои:10.4153 / CJM-1950-035-6, МИСТЕР 0037815.
- ^ а б c d Лежандр, Стефан (2014), «Складки и меандры», Австралазийский журнал комбинаторики, 58: 275–291, arXiv:1302.2025, Bibcode:2013arXiv1302.2025L, МИСТЕР 3211783
- ^ Сент-Лаге, Андре (1937), Avec des nombres et des lignes (на французском языке), Париж: Vuibert, стр. 147–162.. Как цитирует Лежандр (2014)
- ^ а б Гарднер, Мартин (1983), «Комбинаторика складывания бумаги», Колеса, жизнь и другие математические развлечения, Нью-Йорк: W. H. Freeman, стр. 60–73, Bibcode:1983wlom.book ..... G. См., В частности, стр. 60–62.
- ^ Келер, Джон Э. (1968), «Складывание полосы марок», Журнал комбинаторной теории, 5 (2): 135–152, Дои:10.1016 / S0021-9800 (68) 80048-1, МИСТЕР 0228364
- ^ Ланнон, В. Ф. (1968), "Проблема складывания карты", Математика вычислений, 22 (101): 193–199, Дои:10.2307/2004779, JSTOR 2004779, МИСТЕР 0221957
- ^ Дженсен, Иван (2000), «Матричный подход к подсчету плоских меандров», Журнал физики A: математические и общие, 33 (34): 5953, arXiv:cond-mat / 0008178, Bibcode:2000JPhA ... 33,5953J, Дои:10.1088/0305-4470/33/34/301
- ^ Савада, Джо; Ли, Рой (2012), «Складывание штампов, полумеандры и открытые меандры: алгоритмы быстрой генерации», Электронный журнал комбинаторики, 19 (2): Статья 43, 16 стр., МИСТЕР 2946101
- ^ Ди Франческо, П. (2000), "Точная асимптотика меандров", Формальные степенные ряды и алгебраическая комбинаторика (Москва, 2000), Springer, Berlin, стр. 3–14, Дои:10.1007/978-3-662-04166-6_1, ISBN 978-3-642-08662-5, МИСТЕР 1798197
- ^ Коннелли, Роберт; Демейн, Эрик Д.; Роте, Гюнтер (2003), «Выпрямление многоугольных дуг и выпуклость многоугольных циклов» (PDF), Дискретная и вычислительная геометрия, 30 (2): 205–239, Дои:10.1007 / s00454-003-0006-7, МИСТЕР 1931840
- ^ Ланнон, В. Ф. (1971), "Складывание многомерных карт", Компьютерный журнал, 14: 75–80, Дои:10.1093 / comjnl / 14.1.75, МИСТЕР 0285409
- ^ а б Аркин, Эстер М.; Бендер, Майкл А .; Демейн, Эрик Д.; Демейн, Мартин Л.; Митчелл, Джозеф С. Б.; Сетия, Саураб; Скиена, Стивен С. (Сентябрь 2004 г.), "Когда можно сложить карту?" (PDF), Вычислительная геометрия: теория и приложения, 29 (1): 23–46, Дои:10.1016 / j.comgeo.2004.03.012.
- ^ Морган, Томас Д. (21 мая 2012 г.), Складывание карты, Кандидатская диссертация, Массачусетский технологический институт, факультет электротехники и информатики
- ^ Умесато, Такуя; Сайто, Тошики; Уэхара, Рюхей; Ито, Хиро; Окамото, Йошио (2013), «Сложность проблемы складывания штампа», Теоретическая информатика, 497: 13–19, Дои:10.1016 / j.tcs.2012.08.006, МИСТЕР 3084129
внешняя ссылка
- Эрик В. Вайсштейн, Складывание карты (Складной штамп ) в MathWorld.
- «Складывание полосы маркированных марок» из демонстрационного проекта Wolfram Demonstrations Project: http://demonstrations.wolfram.com/FoldingAStripOfLabeledStamps/
