Полюс – нулевой участок - Pole–zero plot

В математика, обработка сигналов и теория управления, а полюс – ноль является графическим представлением рациональный функция передачи в комплексной плоскости, что помогает передать определенные свойства системы, такие как:

Стабильность
Причинная система / антикаузальная система
Регион конвергенции (ROC)
Минимальная фаза / не минимальная фаза

График полюс-ноль показывает положение на комплексной плоскости полюса и нули из функция передачи из динамическая система, например, контроллер, компенсатор, датчик, эквалайзер, фильтр или канал связи. По соглашению, полюса системы обозначены на графике знаком X, а нули обозначены кружком или O.

График «полюс-ноль» может представлять систему с непрерывным (CT) или дискретным (DT) временем. Для системы CT плоскость, в которой появляются полюса и нули, является самолет из Преобразование Лапласа. В этом контексте параметр s представляет сложный угловая частота, которая является областью передаточной функции CT. Для DT-системы плоскость - это плоскость z, где z представляет собой область Z-преобразование.

Системы непрерывного времени

В целом рациональный передаточная функция для непрерывного времени Система LTI имеет вид:

{ displaystyle H (s) = { frac {B (s)} {A (s)}} = { displaystyle sum _ {m = 0} ^ {M} {b_ {m} s ^ {m} } над s ^ {N} + displaystyle sum _ {n = 0} ^ {N-1} {a_ {n} s ^ {n}}} = { frac {b_ {0} + b_ {1 } s + b_ {2} s ^ {2} + cdots + b_ {M} s ^ {M}} {a_ {0} + a_ {1} s + a_ {2} s ^ {2} + cdots + a _ {(N-1)} s ^ {(N-1)} + s ^ {N}}}}

куда

${ displaystyle B}$ и ${ displaystyle A}$ являются многочленами от ${ displaystyle s}$ ,
${ displaystyle M}$ - порядок полинома числителя,
${ displaystyle b_ {m}}$ это м-й коэффициент полинома числителя,
${ displaystyle N}$ - порядок полинома знаменателя, а
${ displaystyle a_ {n}}$ это п-й коэффициент полинома знаменателя.

Либо M, либо N, либо оба могут быть равны нулю, но в реальных системах должно быть так, чтобы ${ Displaystyle M leq N}$ ; в противном случае усиление было бы неограниченным на высоких частотах.

Полюсы и нули

нули системы являются корнями полинома числителя:

 ${ displaystyle s = { beta _ {m} | m in 1, ldots M }}$  такой, что  ${ displaystyle B (s) | _ {s = beta _ {m}} = 0}$

полюса системы являются корнями полинома знаменателя:

 ${ displaystyle s = { alpha _ {n} | n in 1, ldots N }}$  такой, что  ${ displaystyle A (s) | _ {s = alpha _ {n}} = 0}$  .

Область конвергенции

В область конвергенции (ROC) для данной передаточной функции CT представляет собой полуплоскость или вертикальную полосу, каждая из которых не содержит полюсов. В общем, ROC не уникален, и конкретный ROC в каждом конкретном случае зависит от того, является ли система причинный или антипричинные.

Если ОКР включает мнимая ось, то система ограниченный вход, ограниченный выход (BIBO) стабильный.
Если ROC выходит вправо от столба с наибольшим настоящая часть (но не на бесконечности), тогда система причинная.
Если ROC простирается влево от полюса с наименьшей действительной частью (но не на отрицательной бесконечности), то система является антипричинной.

ROC обычно выбирается для включения мнимой оси, поскольку для большинства практических систем важно иметь BIBO стабильность.

Пример

{ displaystyle H (s) = {25 over s ^ {2} + 6s + 25}}

Эта система не имеет (конечных) нулей и двух полюсов:

{ displaystyle s = alpha _ {1} = - 3 + 4j}

и

{ displaystyle s = alpha _ {2} = - 3-4j}

График "полюс-ноль" будет:

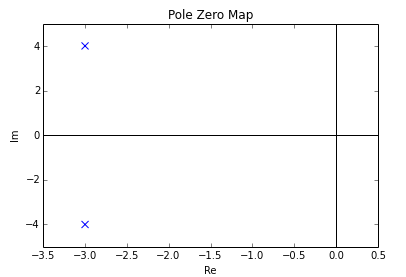
График P-z ранее созданного примера

Обратите внимание, что эти два полюса комплексные конъюгаты, что является необходимым и достаточным условием наличия действительных коэффициентов в дифференциальном уравнении, представляющем систему.

Системы с дискретным временем

В общем, рациональная передаточная функция для дискретного времени Система LTI имеет вид:

{ Displaystyle H (z) = { гидроразрыва {P (z)} {Q (z)}} = { frac { displaystyle sum _ {m = 0} ^ {M} {b_ {m} z ^ {-m}}} {1+ displaystyle sum _ {n = 1} ^ {N} {a_ {n} z ^ {- n}}}} = { frac {b_ {0} + b_ {1 } z ^ {- 1} + b_ {2} z ^ {- 2} cdots + b_ {M} z ^ {- M}} {1 + a_ {1} z ^ {- 1} + a_ {2} z ^ {- 2} cdots + a_ {N} z ^ {- N}}}}

куда

${ displaystyle M}$ - порядок полинома числителя,
${ displaystyle b_ {m}}$ это м-й коэффициент полинома числителя,
${ displaystyle N}$ - порядок полинома знаменателя, а
${ displaystyle a_ {n}}$ это п-й коэффициент полинома знаменателя.

Либо M, либо N, либо оба могут быть равны нулю.

Полюсы и нули

${ displaystyle z = beta _ {m}}$ такой, что ${ Displaystyle P (z) | _ {z = beta _ {m}} = 0}$ являются нули системы
${ displaystyle z = alpha _ {n}}$ такой, что ${ displaystyle Q (z) | _ {z = alpha _ {n}} = 0}$ являются полюса системы.

Область конвергенции

В область конвергенции (ROC) для данной передаточной функции DT является диск или же кольцо который не содержит полюсов. В общем, ROC не уникален, и конкретный ROC в каждом конкретном случае зависит от того, является ли система причинный или антипричинные.

Если ОКР включает единичный круг, то система ограниченный вход, ограниченный выход (BIBO) стабильный.
Если ROC выходит наружу от полюса с наибольшей (но не бесконечной) величиной, то система имеет правосторонний импульсный отклик. Если ROC выходит наружу от полюса с наибольшей величиной и нет полюса на бесконечности, то система является причинной.
Если ROC простирается внутрь от полюса с наименьшей (ненулевой) величиной, то система антипричинна.

ROC обычно выбирается для включения единичного круга, поскольку для большинства практических систем важно иметь BIBO стабильность.

Пример

Если ${ Displaystyle P (z)}$ и ${ displaystyle Q (z)}$ полностью факторизованы, их решение может быть легко отображено в z-плоскость. Например, учитывая следующую передаточную функцию:

{ displaystyle H (z) = { frac {z + 2} {z ^ {2} + { frac {1} {4}}}}}

Единственный (конечный) ноль находится по адресу: ${ displaystyle z = -2}$ , а два полюса расположены по адресу: ${ displaystyle z = pm { frac {j} {2}}}$ , куда j это мнимая единица.

График «полюс – ноль» будет выглядеть следующим образом:

Смотрите также

Библиография

Хааг, Майкл (22 июня 2005 г.). «Понимание графиков полюса / нуля на Z-плоскости». OpenStax CNX. Получено 9 июня, 2018.
Эрик В. Вайсштейн. «Z-преобразование». MathWorld. Получено 24 января, 2010.