Атом Ридберга - Rydberg atom

Рисунок 1: Электронная орбиталь ридберговского атома с п = 12. Цвета показывают квантовую фазу высоковозбужденного электрона.

Фигура 2: Уровни энергии в атомной литий показывающий ряд Ридберга трех самых низких значений орбитальный угловой момент сходящаяся на первой энергии ионизации.

А Атом Ридберга является возбужденный атом с одним или несколькими электроны которые имеют очень высокий главное квантовое число, п.^[1][2] Чем выше значение п, чем дальше электрон от ядра, в среднем. Ридберг атомы обладают рядом специфических свойств, включая преувеличенную реакцию на электрический и магнитные поля,^[3] длительные периоды распада и электрон волновые функции что приблизительное, при некоторых условиях, классический орбиты электронов вокруг ядра.^[4] Электроны ядра экранируют внешний электрон от электрического поля ядра так, что на расстоянии электрический потенциал выглядит идентично тому, которое испытывает электрон в атом водорода.^[5]

Несмотря на свои недостатки, Модель Бора атома полезно для объяснения этих свойств. Классически электрон на круговой орбите радиусом р, о водороде ядро заряда +е, подчиняется Второй закон Ньютона:

${\displaystyle \mathbf {F} =m\mathbf {a} \Rightarrow {ke^{2} \over r^{2}}={mv^{2} \over r}}$

куда k = 1 / (4πε₀ ).

Орбитальный момент равен квантованный в единицах час:

${\displaystyle mvr=n\hbar }$.

Объединение этих двух уравнений приводит к Бор выражение для орбитального радиуса через главное квантовое число, п:

${\displaystyle r={n^{2}\hbar ^{2} \over ke^{2}m}.}$

Теперь очевидно, почему ридберговские атомы обладают такими необычными свойствами: радиус орбиты масштабируется как п² (в п = 137 состояние водорода имеет атомный радиус ~ 1 мкм) и геометрическое сечение как п⁴. Таким образом, ридберговские атомы чрезвычайно велики и слабо связаны. валентность электроны, легко возмущаются или ионизированный столкновениями или внешними полями.

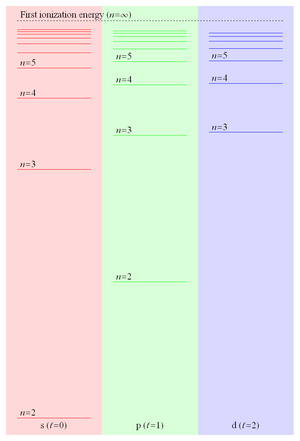
Поскольку энергия связи ридберговского электрона пропорциональна 1 /р и, следовательно, отваливается как 1 /п², расстояние между уровнями энергии уменьшается как 1 /п³ ведущие к еще более близко расположенным уровням, сходящимся на первом энергия ионизации. Эти близко расположенные ридберговские состояния образуют то, что обычно называют Серия Ридберга. фигура 2 показывает некоторые из уровней энергии трех самых низких значений орбитальный угловой момент в литий.

История

Существование серии Ридберга было впервые продемонстрировано в 1885 году, когда Иоганн Балмер обнаружил простая эмпирическая формула для длины волн света, связанного с переходами в атомных водород. Три года спустя шведский физик Йоханнес Ридберг представили обобщенную и более интуитивную версию формулы Бальмера, которая стала известна как Формула Ридберга. Эта формула указала на существование бесконечного ряда все более близко расположенных дискретных уровни энергии сходящийся на конечном пределе.^[6]

Этот ряд качественно объяснил в 1913 г. Нильс Бор с его полуклассическая модель атома водорода, в котором квантованный значения углового момента приводят к наблюдаемым дискретным уровням энергии.^[7][8] Полный количественный вывод наблюдаемого спектра был получен Вольфганг Паули в 1926 г. после разработки квантовая механика к Вернер Гейзенберг и другие.

Способы производства

Единственное по-настоящему стабильное состояние водородоподобный атом это основное состояние с п = 1. Изучение ридберговских состояний требует надежной техники для возбуждения атомов в основном состоянии в состояния с большим значением п.

Возбуждение электронным ударом

Многие ранние экспериментальные работы с ридберговскими атомами основывались на использовании коллимированных пучков быстрых электронов, падающих на атомы в основном состоянии.^[9] Неупругое рассеяние процессы могут использовать электрон кинетическая энергия для увеличения внутренней энергии атомов, возбуждающих широкий диапазон различных состояний, включая многие высоколежащие ридберговские состояния,

${\displaystyle e^{-}+A\rightarrow A^{*}+e^{-}}$.

Поскольку электрон может сохранить любое произвольное количество своей начальной кинетической энергии, в результате этого процесса всегда образуется популяция с широким разбросом различных энергий.

Зарядовое возбуждение

Еще одна опора ранних экспериментов с ридберговскими атомами основывалась на перезарядке между пучком ионы и популяция нейтральных атомов другого вида, что приводит к образованию пучка высоковозбужденных атомов,^[10]

${\displaystyle A^{+}+B\rightarrow A^{*}+B^{+}}$.

Опять же, поскольку кинетическая энергия взаимодействия может вносить вклад в конечную внутреннюю энергию составляющих, этот метод заполняет широкий диапазон энергетических уровней.

Оптическое возбуждение

Появление настраиваемого лазеры на красителях в 1970-х позволил гораздо больший уровень контроля над популяциями возбужденных атомов. При оптическом возбуждении падающий фотон поглощается целевым атомом, абсолютно определяя энергию конечного состояния. Таким образом, задача создания моноэнергетических популяций ридберговских атомов в одном состоянии становится несколько более простой задачей точного управления частотой выходного лазерного излучения.

${\displaystyle A+\gamma \rightarrow A^{*}}$.

Эта форма прямого оптического возбуждения обычно ограничивается экспериментами с щелочных металлов, потому что основное состояние энергия связи у других видов, как правило, слишком высок, чтобы быть доступным для большинства лазерных систем.

Для атомов с большим валентный электрон энергия связи (эквивалент большого первого энергия ионизации ) возбужденные состояния серии Ридберга недоступны для обычных лазерных систем. Первоначальное столкновительное возбуждение может восполнить дефицит энергии, позволяя использовать оптическое возбуждение для выбора конечного состояния. Хотя на начальном этапе происходит возбуждение в широком диапазоне промежуточных состояний, точность, присущая процессу оптического возбуждения, означает, что лазерный свет взаимодействует только с определенным подмножеством атомов в определенном состоянии, возбуждая до выбранного конечного состояния.

Водородный потенциал

Основная статья: Атом водорода

Рисунок 3. Сравнение потенциала в атоме водорода с потенциалом в ридберговском состоянии другого атома. Была использована большая поляризуемость сердечника, чтобы сделать эффект ясным. Черная кривая - кулоновская 1 /р потенциала атома водорода, а красная пунктирная кривая включает 1 /р⁴ член из-за поляризации ионного остова.

Атом в Состояние Ридберга имеет валентность электрон на большой орбите вдали от ионного остова; на такой орбите крайний электрон чувствует почти гидрогенный, Кулон потенциал, U_C из компактного ионного остова, состоящего из ядро с участием Z протоны а нижние электронные оболочки заполнены Z-1 электрон. Электрон в сферически-симметричном кулоновском потенциале обладает потенциальной энергией:

${\displaystyle U_{\text{C}}=-{\dfrac {e^{2}}{4\pi \varepsilon _{0}r}}}$.

Сходство эффективного потенциала, «видимого» внешним электроном, с потенциалом водорода является определяющей характеристикой Ридберг заявляет и объясняет, почему электронные волновые функции приближаются к классическим орбитам в пределе принцип соответствия.^[11] Другими словами, орбита электрона напоминает орбиту планет внутри солнечной системы, похожую на то, что было замечено в устаревших, но визуально полезных. Бор и Резерфорд модели атома.

Есть три заметных исключения, которые можно охарактеризовать добавлением дополнительного члена к потенциальной энергии:

• Атом может иметь два (или более) электрона в высоковозбужденных состояниях с сопоставимыми радиусами орбиты. В этом случае электрон-электронное взаимодействие приводит к значительному отклонению от водородного потенциала.^[12] Для атома в кратном ридберговском состоянии дополнительный член U_ее, включает суммирование каждого пара высоковозбужденных электронов:

${\displaystyle U_{ee}={\dfrac {e^{2}}{4\pi \varepsilon _{0}}}\sum _{i<j}{\dfrac {1}{|\mathbf {r} _{i}-\mathbf {r} _{j}|}}}$.

• Если валентный электрон имеет очень низкий угловой момент (классически интерпретируемый как чрезвычайно эксцентричный эллиптическая орбита), то он может пройти достаточно близко, чтобы поляризовать ионный остов, вызывая 1 /р⁴ член поляризации ядра в потенциале.^[13] Взаимодействие между индуцированный диполь и заряд, который производит это, всегда привлекателен, поэтому этот вклад всегда отрицателен,

${\displaystyle U_{\text{pol}}=-{\dfrac {e^{2}\alpha _{\text{d}}}{(4\pi \varepsilon _{0})^{2}r^{4}}}}$,

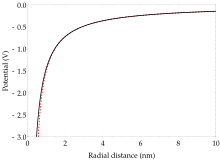
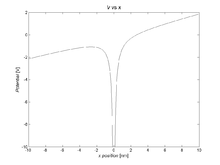
где α_d это диполь поляризуемость. Рисунок 3 показывает, как поляризационный член изменяет потенциал вблизи ядра.

• Если внешний электрон проникает через внутренние электронные оболочки, он «видит» больше заряда ядра и, следовательно, испытывает большую силу. В общем, изменение потенциальной энергии непросто вычислить и должно основываться на знании геометрии ионного остова.^[14]

Квантово-механические детали

Рисунок 4. Полуклассические орбиты для п= 5 со всеми допустимыми значениями орбитального углового момента. Черное пятно обозначает положение атомного ядра.

Квантово-механически состояние с аномально высоким п относится к атому, в котором валентный электрон (ы) был возбужден в ранее незаселенный электронная орбиталь с большей энергией и ниже энергия связи. В водороде энергия связи определяется выражением:

${\displaystyle E_{\text{B}}=-{\dfrac {Ry}{n^{2}}}}$,

куда Ry = 13.6 эВ это Постоянная Ридберга. Низкая энергия связи при высоких значениях п объясняет, почему ридберговские состояния подвержены ионизации.

Дополнительные члены в выражении потенциальной энергии для ридберговского состояния, помимо водородной кулоновской потенциальной энергии, требуют введения квантовый дефект,^[5] δ_л, в выражение для энергии связи:

${\displaystyle E_{\text{B}}=-{\dfrac {Ry}{(n-\delta _{l})^{2}}}}$.

Электронные волновые функции

Большое время жизни ридберговских состояний с высоким орбитальным угловым моментом можно объяснить с точки зрения перекрытия волновых функций. Волновая функция электрона в высоком л Состояние (высокий угловой момент, «круговая орбита») очень мало перекрывается с волновыми функциями внутренних электронов и, следовательно, остается относительно невозмущенным.

Три исключения из определения ридберговского атома как атома с водородным потенциалом имеют альтернативное квантово-механическое описание, которое может быть охарактеризовано дополнительным членом (ами) в атомном Гамильтониан:

• Если второй электрон возбужден в состояние п_я, энергетически близкое к состоянию внешнего электрона п_о, то его волновая функция становится почти такой же большой, как первая (двойное ридберговское состояние). Это происходит как п_я подходы п_о и приводит к состоянию, когда размеры орбит двух электронов связаны;^[12] состояние, которое иногда называют радиальная корреляция.^[1] Член электрон-электронного отталкивания должен быть включен в гамильтониан атома.
• Поляризация ионного ядра дает анизотропный потенциал, который вызывает угловая корреляция между движениями двух крайних электронов.^[1][15] Это можно рассматривать как приливная блокировка эффект из-за несферически симметричного потенциала. Член поляризации ядра должен быть включен в атомный гамильтониан.
• Волновая функция внешнего электрона в состояниях с малым орбитальным угловым моментом л, периодически локализуется в оболочках внутренних электронов и взаимодействует с полным зарядом ядра.^[14] Рисунок 4 показывает полуклассический интерпретация состояний углового момента на электронной орбитали, иллюстрирующая эту низкуюл состояния проходят ближе к ядру, потенциально проникая в ионный остов. К атомному гамильтониану необходимо добавить член проникновения в ядро.

Во внешних полях

Рисунок 5. Расчетные спектры уровней энергии водорода в электрическом поле вблизи п=15.^[16] Потенциальная энергия, найденная в электронном гамильтониане для водорода, равна 1 /р Кулоновский потенциал (нет квантового дефекта), который не связывает различные штарковские состояния. Следовательно, уровни энергии из соседних п-многообразия пересекаются в пределе Инглиса – Теллера.

Рисунок 6. Расчетные спектры уровней энергии лития в электрическом поле вблизи п=15.^[16] Наличие ионного остова, который может быть поляризован и пронизан ридберговским электроном, добавляет дополнительные члены к электронному гамильтониану (что приводит к конечному квантовому дефекту), что приводит к взаимодействию различных штарковских состояний и, следовательно, избегать переходов уровней энергии.

Большое расстояние между электроном и ионным остовом в ридберговском атоме делает возможным чрезвычайно большое электрический дипольный момент, d. Есть энергия, связанная с наличием электрического диполя в электрическое поле, F, известный в атомной физике как Полный сдвиг,

${\displaystyle E_{\text{S}}=-\mathbf {d} \cdot \mathbf {F} .}$

В зависимости от знака проекции дипольного момента на вектор локального электрического поля состояние может иметь энергию, которая увеличивается или уменьшается с увеличением напряженности поля (состояния поиска слабого поля и сильного поля соответственно). Узкое расстояние между соседними п-уровни в ряду Ридберга означают, что состояния могут приближаться вырождение даже для относительно скромных значений напряженности поля. Теоретическая напряженность поля, при которой произойдет пересечение, если предположить отсутствие связи между состояниями, определяется выражением Предел Инглиса – Теллера,^[17]

${\displaystyle F_{\text{IT}}={\dfrac {e}{12\pi \varepsilon _{0}a_{0}^{2}n^{5}}}.}$

в атом водорода, чистый 1 /р Кулоновский потенциал не связывает штарковские состояния из соседних п-многообразия, приводящие к реальным пересечениям, как показано на цифра 5. Наличие дополнительных членов в потенциальной энергии может привести к взаимодействию, что приведет к предотвращению пересечений, как показано для литий в рисунок 6.

Приложения и дальнейшие исследования

Прецизионные измерения захваченных ридберговских атомов

Время жизни радиационного распада атомов из метастабильных состояний в основное состояние важно для понимания астрофизических наблюдений и проверки стандартной модели.^[18]

Исследование диамагнитных эффектов

Большие размеры и низкие энергии связи ридберговских атомов приводят к высокой магнитная восприимчивость, ${\displaystyle \chi }$. Поскольку диамагнитные эффекты масштабируются с площадью орбиты, а площадь пропорциональна квадрату радиуса (А ∝ п⁴), эффекты, которые невозможно обнаружить в атомах основного состояния, становятся очевидными в атомах Ридберга, которые демонстрируют очень большие диамагнитные сдвиги.^[19]

Атомы Ридберга демонстрируют сильную электрическую дипольную связь атомов с электромагнитными полями и использовались для обнаружения радиосвязи.^[20][21]

В плазме

Ридберговские атомы обычно образуются в плазма за счет рекомбинации электронов и положительных ионов; рекомбинация с низкой энергией приводит к довольно стабильным ридберговским атомам, в то время как рекомбинация электронов и положительных ионов с высокой кинетическая энергия часто образуют автоионизация Ридберг констатирует. Большие размеры ридберговских атомов и их восприимчивость к возмущениям и ионизации электрическими и магнитными полями являются важным фактором, определяющим свойства плазмы.^[22]

Конденсация ридберговских атомов образует Ридберг дело, чаще всего наблюдаются в виде долгоживущих кластеров. Девозбуждению в ридберговской материи значительно препятствуют обменно-корреляционные эффекты в неоднородной электронной жидкости, образующейся при конденсации коллективными валентными электронами, что приводит к увеличению времени жизни кластеров.^[23]

В астрофизике

Это было предложено^[24] что ридберговские атомы обычны в межзвездном пространстве и их можно наблюдать с Земли. Поскольку плотность межзвездных газовых облаков очень велика. порядки величины ниже, чем самый лучший лабораторный вакуум, достижимый на Земле, состояния Ридберга могут сохраняться в течение длительных периодов времени, не разрушаясь при столкновениях.

Сильно взаимодействующие системы

Из-за своего большого размера ридберговские атомы могут иметь очень большие размеры. электрические дипольные моменты. Расчеты с использованием теория возмущений показывают, что это приводит к сильному взаимодействию между двумя близкими ридберговскими атомами. Последовательный контроль этих взаимодействий в сочетании с их относительно долгим сроком службы делает их подходящим кандидатом для реализации квантовый компьютер.^[25] В 2010 году два-кубит ворота были получены экспериментально.^[26][27] Сильно взаимодействующие ридберговские атомы также имеют квантово-критический поведение, что делает их интересными для самостоятельного изучения.^[28]

Текущие направления исследований

С 2000-х годов исследования ридберговских атомов охватывают три основных направления: зондирование, квантовая оптика и квантовое моделирование ^[2]. Высокие электрические дипольные моменты между состояниями ридберговских атомов используются для радиочастот и терагерц зондирование и отображение^[29][30], включая неразрушающие измерения отдельных микроволновых фотонов^[31]. Электромагнитно индуцированная прозрачность был использован в сочетании с сильными взаимодействиями между двумя атомами, возбужденными в состоянии Ридберга, для создания среды, которая демонстрирует сильно нелинейное поведение на уровне отдельных оптических фотонов. ^[32][33]. Настраиваемое взаимодействие между ридберговскими состояниями позволило также провести первые эксперименты по квантовому моделированию.^[34][35].

В октябре 2018 г. Исследовательская лаборатория армии США публично обсуждал усилия по разработке сверхширокополосного радиоприемника с использованием ридберговских атомов.^[36] В марте 2020 года лаборатория объявила, что ее ученые проанализировали чувствительность датчика Ридберга к осциллирующим электрическим полям в огромном диапазоне частот - от 0 до 10-12 герц (спектр до длины волны 0,3 мм). Датчик Ридберга может надежно обнаруживать сигналы по всему спектру и выгодно отличаться от других известных технологий датчиков электрического поля, таких как электрооптические кристаллы и пассивная электроника с дипольной антенной.^[37]

Классический симулятор

Рисунок 7. Потенциал Штарка - Кулона для ридберговского атома в статическом электрическом поле. Электрон в таком потенциале ощущает крутящий момент, который может изменить его угловой момент.

Рисунок 8. Траектория электрон в атом водорода в электрическое поле E = -3 х 10⁶ В / м в Икс-направление. Обратите внимание, что классически допустимы все значения углового момента; фигура 4 показывает конкретные орбиты, связанные с квантово-механически допустимыми значениями. Увидеть анимация.

Простой 1 /р потенциальные результаты в закрытом Кеплеровская эллиптическая орбита. При наличии внешнего электрическое поле Атомы Ридберга могут получить очень большие электрические дипольные моменты что делает их чрезвычайно восприимчивыми к возмущениям поля. Рисунок 7 показывает, как приложение внешнего электрического поля (известного в атомной физике как Старк поле) меняет геометрию потенциала, резко меняя поведение электрона. Кулоновский потенциал не применяется крутящий момент поскольку сила всегда антипараллельный в вектор положения (всегда указывающий вдоль линии, проходящей между электроном и ядром):

${\displaystyle |\mathbf {\tau } |=|\mathbf {r} \times \mathbf {F} |=|\mathbf {r} ||\mathbf {F} |\sin \theta }$,

${\displaystyle \theta =\pi \Rightarrow \mathbf {\tau } =0}$.

При приложении статического электрического поля электрон ощущает непрерывно изменяющийся крутящий момент. Результирующая траектория со временем становится все более искаженной, в конечном итоге проходя через весь диапазон углового момента от L = L_{МАКСИМУМ}, к прямой L= 0, на начальную орбиту в обратном смысле L = -L_{МАКСИМУМ}.^[38]

Период времени колебания углового момента (время завершения траектории в рисунок 8), почти точно соответствует квантово-механическому предсказанному периоду возврата волновой функции в исходное состояние, демонстрируя классическую природу ридберговского атома.

Смотрите также

• Тяжелая система Ридберга
• Старая квантовая теория
• Квантовый хаос
• Молекула Ридберга
• Ридберг полярон

Рекомендации

1. Галлахер, Томас Ф. (1994). Ридберг Атомы. Издательство Кембриджского университета. ISBN  978-0-521-02166-1.
2. Шибалич, Никола; С. Адамс, Чарльз (2018). Ридберг Физика. IOP Publishing. Bibcode:2018ryph.book ..... S. Дои:10.1088/978-0-7503-1635-4. ISBN  9780750316354.
3. Metcalf Research Group (2004-11-08). «Ридберг Атом Оптикс». Университет Стоуни-Брук. Архивировано из оригинал 26 августа 2005 г.. Получено 2008-07-30.
4. Дж. Мюррей-Крезан (2008). «Классическая динамика ридберговских штарковских атомов в импульсном пространстве». Американский журнал физики. 76 (11): 1007–1011. Bibcode:2008AmJPh..76.1007M. Дои:10.1119/1.2961081.
5. Нолан, Джеймс (31 мая 2005 г.). «Ридберговские атомы и квантовый дефект». Дэвидсон колледж. Получено 2008-07-30.
6. И. Мартинсон; и другие. (2005). «Янне Ридберг - его жизнь и творчество». Ядерные приборы и методы в физических исследованиях Секция B. 235 (1–4): 17–22. Bibcode:2005НИМПБ.235 ... 17М. Дои:10.1016 / j.nimb.2005.03.137.
7. "Модель Бора". Университет Теннесси, Ноксвилл. 2000-08-10. Получено 2009-11-25.
8. Нильс Бор (1922-12-11). «Строение атома» (PDF). Нобелевская лекция. Получено 2018-11-16.
9. Дж. Олмстед (1967). «Возбуждение триплетных состояний азота электронным ударом». Радиационные исследования. 31 (2): 191–200. Bibcode:1967RadR ... 31..191O. Дои:10.2307/3572319. JSTOR  3572319. PMID  6025857.
10. M. Haugh и др. (1966). «Электронное возбуждение при перезарядке». Журнал химической физики. 44 (2): 837–839. Bibcode:1966JChPh..44..837H. Дои:10.1063/1.1726773.
11. Т. П. Хезель и др. (1992). «Классический взгляд на свойства ридберговских атомов: применение принципа соответствия». Американский журнал физики. 60 (4): 329–335. Bibcode:1992AmJPh..60..329H. Дои:10.1119/1.16876.
12. Дмитриева И. К.; и другие. (1993). "Энергии двояковозбужденных состояний. Двойная формула Ридберга". Журнал прикладной спектроскопии. 59 (1–2): 466–470. Bibcode:1993JApSp..59..466D. Дои:10.1007 / BF00663353.
13. Л. Нил; и другие. (1995). «Поляризация ядра в Kr VIII». Физический обзор A. 51 (5): 4272–4275. Bibcode:1995ПхРвА..51.4272Н. Дои:10.1103 / PhysRevA.51.4272. PMID  9912104.
14. К. Э. Теодосиу (1983). «Оценка эффектов проникновения вл Ридберг заявляет ". Физический обзор A. 28 (5): 3098–3101. Bibcode:1983ПхРвА..28.3098Т. Дои:10.1103 / PhysRevA.28.3098.
15. Т. А. Хайм; и другие. (1995). «Возбуждение высоколежащих парно-ридберговских состояний». Журнал физики B. 28 (24): 5309–5315. Bibcode:1995JPhB ... 28.5309H. Дои:10.1088/0953-4075/28/24/015.
16. М. Кортни и др. (1995). «Классическая, полуклассическая и квантовая динамика лития в электрическом поле». Физический обзор A. 51 (5): 3604–3620. Bibcode:1995PhRvA..51.3604C. Дои:10.1103 / PhysRevA.51.3604. PMID  9912027.
17. D.R. Инглис; и другие. (1939). «Ионное снижение пределов рядов в одноэлектронных спектрах». Астрофизический журнал. 90: 439. Bibcode:1939ApJ .... 90..439I. Дои:10.1086/144118.
18. Николас Д. Гиз; и другие. (24 апреля, 2014). «Измерение времени жизни Kr xviii 3d 2D5 / 2 при низкой энергии в унитарной ловушке Пеннинга». Phys. Ред. А. 89 (4): 040502. arXiv:1404.6181. Bibcode:2014PhRvA..89d0502G. Дои:10.1103 / PhysRevA.89.040502.
19. J. Neukammer и др. (1984). «Диамагнитный сдвиг и синглет-триплетное смешение 6sпp Yb Ридберговские состояния большой радиальной протяженности ». Физический обзор A. 30 (2): 1142–1144. Bibcode:1984ПхРвА..30.1142Н. Дои:10.1103 / PhysRevA.30.1142.
20. Андерсон, Дэвид А .; и другие. (26 августа 2018 г.). «Атомный приемник для AM и FM радиосвязи». arXiv:1808.08589 [Physics.atom-ph ].
21. Улетт, Дженнифер (19 сентября 2018 г.). «Новая антенна, использующая отдельные атомы, может открыть эру атомного радио». Ars Technica. Получено 19 сентября 2018.
22. G. Vitrant, et al. (1982). «Ридберг к эволюции плазмы в плотном газе из очень возбужденных атомов». Журнал физики B. 15 (2): L49 – L55. Bibcode:1982JPhB ... 15л..49В. Дои:10.1088/0022-3700/15/2/004.
23. Маныкин Е.А. и др. (2006). «Ридберговское вещество: свойства и распад». Труды SPIE. Труды SPIE. 6181 (5): 618105–618105–9. Bibcode:2006SPIE.6181E..05M. Дои:10.1117/12.675004.
24. Ю. Н. Гнедин и др. (2009). «Ридберговские атомы в астрофизике». Новые обзоры астрономии. 53 (7–10): 259–265. arXiv:1208.2516. Bibcode:2009NewAR..53..259G. Дои:10.1016 / j.newar.2009.07.003.
25. Д. Якш и др. (2000). «Быстрые квантовые ворота для нейтральных атомов». Письма с физическими проверками. 85 (10): 2208–11. arXiv:Quant-ph / 0004038. Bibcode:2000PhRvL..85.2208J. Дои:10.1103 / PhysRevLett.85.2208. PMID  10970499.
26. T. Wilk, et al. (2010).«Запутывание двух отдельных нейтральных атомов с помощью блокады Ридберга». Письма с физическими проверками. 104 (1): 010502. arXiv:0908.0454. Bibcode:2010PhRvL.104a0502W. Дои:10.1103 / PhysRevLett.104.010502. PMID  20366354.
27. Л. Изенхауэр и др. (2010). «Демонстрация квантового затвора, управляемого нейтральным атомом, а не квантового затвора». Письма с физическими проверками. 104 (1): 010503. arXiv:0907.5552. Bibcode:2010PhRvL.104a0503I. Дои:10.1103 / PhysRevLett.104.010503. PMID  20366355.
28. H. Weimer и др. (2008). «Квантово-критическое поведение в сильно взаимодействующих ридберговских газах». Письма с физическими проверками. 101 (25): 250601. arXiv:0806.3754. Bibcode:2008PhRvL.101y0601W. Дои:10.1103 / PhysRevLett.101.250601. PMID  19113686.
29. Sedlacek, Jonathon A .; Шветтманн, Арне; Кюблер, Харальд; Лёв, Роберт; Пфау, Тильман; Шаффер, Джеймс П. (2012-09-16). «Микроволновая электрометрия с ридберговскими атомами в паровой ячейке с использованием ярких атомных резонансов». Природа Физика. 8 (11): 819–824. Bibcode:2012НатФ ... 8..819С. Дои:10.1038 / nphys2423. ISSN  1745-2473.
30. Wade, C.G .; Šibalić, N .; de Melo, N.R .; Kondo, J.M .; Adams, C. S .; Уэзерилл, К. Дж. (07.11.2016). «Терагерцовое изображение в ближнем поле в реальном времени с атомной оптической флуоресценцией». Природа Фотоника. 11 (1): 40–43. arXiv:1603.07107. Дои:10.1038 / nphoton.2016.214. ISSN  1749-4885.
31. Nogues, G .; Rauschenbeutel, A .; Оснаги, С .; Brune, M .; Raimond, J.M .; Гарош, С. (1999). «Видеть одиночный фотон, не разрушая его». Природа. 400 (6741): 239–242. Bibcode:1999Натура 400..239Н. Дои:10.1038/22275. ISSN  0028-0836.
32. Pritchard, J.D .; Максвелл, Д .; Gauguet, A .; Weatherill, K. J .; Джонс, М. П. А .; Адамс, С. С. (05.11.2010). «Кооперативное взаимодействие атома-света в блокированном ансамбле Ридберга». Письма с физическими проверками. 105 (19): 193603. arXiv:0911.3523. Bibcode:2010ПхРвЛ.105с3603П. Дои:10.1103 / Physrevlett.105.193603. ISSN  0031-9007. PMID  21231168.
33. Фирстенберг, Офер; Пейронель, Тибо; Лян, Ци-Ю; Горшков, Алексей В .; Лукин, Михаил Д .; Вулетич, Владан (25 сентября 2013 г.). «Притягивающие фотоны в квантовой нелинейной среде» (PDF). Природа. 502 (7469): 71–75. Bibcode:2013Натура 502 ... 71F. Дои:10.1038 / природа12512. ISSN  0028-0836. PMID  24067613.
34. Schauß, P .; Zeiher, J .; Fukuhara, T .; Hild, S .; Cheneau, M .; Macrì, T .; Pohl, T .; Bloch, I .; Гросс, К. (27 марта 2015 г.). «Кристаллизация в квантовых магнитах Изинга». Наука. 347 (6229): 1455–1458. arXiv:1404.0980. Дои:10.1126 / science.1258351. ISSN  0036-8075. PMID  25814579.
35. Лабун, Хеннинг; Барредо, Даниэль; Равец, Сильвен; де Лезелёк, Сильвен; Макри, Томмазо; Лахайе, Тьерри; Брауэйс, Антуан (2016). «Настраиваемые двумерные массивы одиночных ридберговских атомов для реализации квантовых моделей Изинга». Природа. 534 (7609): 667–670. arXiv:1509.04543. Bibcode:2016Натура.534..667L. Дои:10.1038 / природа18274. ISSN  0028-0836. PMID  27281203.
36. Армейские исследователи совершили гигантский скачок в области квантового зондирования, Исследовательская лаборатория армии США, 2018-10-25
37. Ученые создали квантовый датчик, охватывающий весь радиочастотный спектр, Phys.org /Исследовательская лаборатория армии США, 2020-03-19
38. Т. П. Хезель и др. (1992). «Классический взгляд на эффект Штарка в атомах водорода». Американский журнал физики. 60 (4): 324–328. Bibcode:1992AmJPh..60..324H. Дои:10.1119/1.16875.