Метод ходьбы по сферам - Walk-on-spheres method

В математика, то метод прогулки по сферам (WoS) числовой вероятностный алгоритм, или же Метод Монте-Карло, используемый в основном для аппроксимации решений некоторых конкретных краевая задача за уравнения в частных производных (PDE).^[1][2] Метод WoS был впервые представлен Мервин Э. Мюллер в 1956 году решить Уравнение Лапласа,^[1] и с тех пор был распространен на другие проблемы.

Он полагается на вероятностную интерпретацию PDE и моделирует пути Броуновское движение (или для некоторых более общих вариантов, диффузионные процессы ), выбирая только точки выхода из следующих друг за другом сфер, а не моделируя подробно путь процесса. Это часто делает его менее затратным, чем "сеточные" алгоритмы, и сегодня это один из наиболее широко используемых алгоритмов "без сетки" для генерации броуновских путей.

Неформальное описание

Позволять ${\displaystyle \Omega }$ быть ограниченным домен в ${\displaystyle \mathbb {R} ^{d}}$ с достаточно регулярной границей ${\displaystyle \Gamma }$, позволять час быть функцией на ${\displaystyle \Gamma }$, и разреши ${\displaystyle x}$ быть точкой внутри ${\displaystyle \Omega }$.

Рассмотрим Задача Дирихле:

${\displaystyle {\begin{cases}\Delta u(x)=0&{\mbox{if }}x\in \Omega \\u(x)=h(x)&{\mbox{if }}x\in \Gamma .\end{cases}}}$

Это легко показать^[а] что когда решение ${\displaystyle u}$ существует, для ${\displaystyle x\in \Omega }$:

${\displaystyle u(x)=\mathbb {E} _{x}[h(W_{\tau })]}$

куда W это d-размерный Винеровский процесс, математическое ожидание берется условно на {W₀ = Икс}, и τ время первого выхода из Ω.

Чтобы вычислить решение с использованием этой формулы, нам нужно только смоделировать первую точку выхода независимых броуновских путей, поскольку закон больших чисел:

${\displaystyle \mathbb {E} _{x}[h(W_{\tau })]\sim {\frac {1}{n}}\sum _{i=1}^{n}h(W_{\tau }^{i})}$

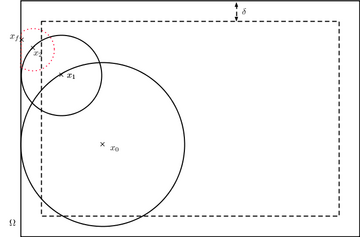
Метод WoS обеспечивает эффективный способ выборки первой точки выхода броуновского движения из области, отмечая, что для любого (d − 1)-сфера сосредоточена на Икс, первая точка выхода из W вне сферы имеет равномерное распределение по ее поверхности. Таким образом, он начинается с Икс⁽⁰⁾ равно Икс, и рисует самую большую сферу ${\displaystyle {\mathcal {S}}_{0}}$ сосредоточен на Икс⁽⁰⁾ и содержится внутри домена. Первая точка выхода Икс⁽¹⁾ из ${\displaystyle {\mathcal {S}}_{0}}$ равномерно распределяется по его поверхности. Повторяя этот шаг индуктивно, WoS выдает последовательность (Икс^(п)) позиций броуновского движения.

Согласно интуиции, процесс сведется к первой точке выхода из области. Однако этот алгоритм почти наверняка требует бесконечного количества шагов для завершения. Для вычислительной реализации процесс обычно останавливается, когда он подходит достаточно близко к границе, и возвращает проекцию процесса на границе. Эту процедуру иногда называют введением ${\displaystyle \varepsilon }$-оболочка, или ${\displaystyle \varepsilon }$-слой.^[4]

Формулировка метода

Иллюстрация запуска алгоритма прогулки по сферам в произвольной области ${\displaystyle \Omega }$ с ${\displaystyle \varepsilon }$-ракушка

выбирать ${\displaystyle \varepsilon >0}$. Используя те же обозначения, что и выше, алгоритм прогулки по сферам описывается следующим образом:

1. Инициализировать: ${\displaystyle x^{(0)}=x}$
2. Пока ${\displaystyle d(x^{(n)},\Gamma )>\varepsilon }$:
   1. Набор ${\displaystyle r_{n}=d(x^{(n)},\Gamma )}$.
   2. Образец ${\displaystyle \gamma _{n}}$ вектор, равномерно распределенный по единичной сфере, независимо от предыдущих.
   3. Набор ${\displaystyle x^{(n+1)}:=x^{(n)}+r_{n}\gamma _{n}}$
3. Когда ${\displaystyle d(x^{(n)},\Gamma )\leq \varepsilon }$:
4. ${\displaystyle x_{f}:=p_{\Gamma }(x^{(n)})}$, ортогональная проекция ${\displaystyle x^{(n)}}$ на ${\displaystyle \Gamma }$
5. Возвращаться ${\displaystyle x_{f}}$

Результат ${\displaystyle x_{f}}$ оценка первой точки выхода из ${\displaystyle \Omega }$ винеровского процесса, начиная с ${\displaystyle x}$в том смысле, что они имеют близкое распределение вероятностей (см. ниже комментарии к ошибке).

Комментарии и практические соображения

Радиус сфер

В некоторых случаях расстояние до границы может быть трудно вычислить, и в этом случае предпочтительнее заменить радиус сферы нижней границей этого расстояния. Затем необходимо убедиться, что радиус сфер остается достаточно большим, чтобы процесс достиг границы.^[1]

Смещение в методе и GFFP

Метод Walk-on-Spheres используется до тех пор, пока процесс не станет ${\displaystyle \delta }$-Близко к границе. Затем сфера заменяется ее «пересечением» с границей области.

Поскольку это метод Монте-Карло, погрешность оценки может быть разложена на сумму предвзятость, а статистическая ошибка. Статистическая ошибка уменьшается за счет увеличения количества выбранных путей или использования уменьшение дисперсии методы.

WoS теоретически обеспечивает точное (или беспристрастное) моделирование траекторий броуновского движения. Однако, как здесь сформулировано, ${\displaystyle \varepsilon }$-shell, введенный, чтобы гарантировать, что алгоритм завершается, также добавляет ошибку, обычно порядка ${\displaystyle {\mathcal {O}}(\varepsilon )}$.^[4] Эта ошибка была изучена, и ее можно избежать в некоторых геометриях, используя Функции Грина Метод первого прохода:^[5] можно изменить геометрию «сфер», когда они находятся достаточно близко к границе, так что вероятность достижения границы за один шаг становится положительной. Это требует знания функций Грина для конкретных областей. (смотрите также Гармоническая мера )

Когда это возможно, Функция Грина Метод первого прохода (GFFP) обычно предпочтительнее, так как он быстрее и точнее, чем классический WoS.^[4]

Сложность

Можно показать, что количество шагов, сделанных для того, чтобы процесс WoS достиг ${\displaystyle \varepsilon }$-оболочка в порядке ${\displaystyle {\mathcal {O}}(|\log(\varepsilon )|)}$.^[2] Следовательно, можно до некоторой степени повысить точность без значительного увеличения числа шагов.

Как это обычно бывает с методами Монте-Карло, этот алгоритм особенно хорошо работает, когда размерность больше, чем ${\displaystyle 3}$, и нужен только небольшой набор значений. Действительно, вычислительные затраты линейно возрастают с увеличением размера, тогда как стоимость методов, зависящих от сетки, увеличивается экспоненциально с увеличением размера.^[2]

Варианты, расширения

Этот метод широко изучен, обобщен и усовершенствован. Например, сейчас он широко используется для вычисления физических свойств материалов (таких как емкость, внутренняя электростатическая энергия молекул и др.). Некоторые известные расширения включают:

Эллиптические уравнения

Метод WoS может быть изменен для решения более общих задач. В частности, метод был обобщен для решения задач Дирихле для уравнений вида ${\displaystyle \Delta u=cu+f}$ ^[6] (которые включают Пуассон и линеаризованный Пуассона-Больцмана уравнений) или для любых эллиптическое уравнение в частных производных с постоянными коэффициентами.^[7]

Также были разработаны более эффективные способы решения линеаризованного уравнения Пуассона – Больцмана, основанные на Фейнман-Кац представления решений.^[8]

Зависимость от времени

Опять же, в пределах достаточно регулярной границы можно использовать метод WoS для решения следующей проблемы:

${\displaystyle {\begin{cases}\partial _{t}u(x,t)+{\frac {1}{2}}\Delta _{x}u(x,t)=0&{\mbox{if }}x\in \Omega {\mbox{and }}t<T\\u(x,T)=h(x,T)&{\mbox{if }}x\in {\bar {\Omega }}\\u(x,t)=h(x,t)&{\mbox{if }}x\in \Gamma .\end{cases}}}$

решение которого можно представить в виде:^[9]

${\displaystyle u(x,t)=\mathbb {E} _{t,x}(h(X_{T\wedge \tau },T\wedge \tau ))}$,

где ожидание принято условно от ${\displaystyle X_{t}=x}$

Чтобы использовать WoS по этой формуле, необходимо выбрать время выхода из каждой нарисованной сферы, которая является независимой переменной. ${\displaystyle \tau _{0}}$ с преобразованием Лапласа (для сферы радиуса ${\displaystyle R}$):^[10]

${\displaystyle \mathbb {E} (\exp(-s\tau _{0})))={\frac {R{\sqrt {2s}}}{\sinh(R{\sqrt {2s}})}}}$

Общее время выхода из домена ${\displaystyle \tau }$ можно вычислить как сумму времен выхода из сфер. Процесс также должен быть остановлен, если он не покинул домен во время ${\displaystyle T}$.

Прочие расширения

Метод WoS был обобщен для оценки решения эллиптических уравнений в частных производных повсюду в области, а не в одной точке.^[11]

Метод WoS также был обобщен для вычисления времени срабатывания для процессов, отличных от броуновских движений. Например, время попадания Бесселевские процессы может быть вычислен с помощью алгоритма под названием «Прогулка по движущимся сферам».^[12] Эта проблема имеет приложения в финансовой математике.

Наконец, WoS может быть адаптирован для решения уравнений Пуассона и Пуассона – Больцмана с условиями потока на границе.^[13]

Смотрите также

• Формула Фейнмана – Каца
• Случайные процессы и краевые задачи
• Метод Эйлера – Маруямы пробовать пути общих диффузионных процессов

Примечания

1. Связь была впервые установлена ​​Какутани для двумерного броуновского движения,^[3] теперь его можно рассматривать как тривиальный случай формулы Фейнмана-Каца.

Рекомендации

1. Мюллер, Мервин Э. (Сентябрь 1956 г.). "Некоторые непрерывные методы Монте-Карло для задачи Дирихле". Анналы математической статистики. 27 (3): 569–589. Дои:10.1214 / aoms / 1177728169. JSTOR  2237369.
2. Сабельфельд, Карл К. (1991). Методы Монте-Карло в краевых задачах. Берлин [и др.]: Springer-Verlag. ISBN  978-3540530015.
3. Какутани, Шизуо (1944). «Двумерное броуновское движение и гармонические функции». Известия Императорской Академии. 20 (10): 706–714. Дои:10.3792 / pia / 1195572706.
4. Масканьи, Майкл; Хван, Чи-Ок (июнь 2003 г.). «Анализ ошибок ϵ-оболочки для алгоритмов« Прогулки по сферам »». Математика и компьютеры в моделировании. 63 (2): 93–104. Дои:10.1016 / S0378-4754 (03) 00038-7.
5. Учитывая, Джеймс А .; Хаббард, Джозеф Б .; Дуглас, Джек Ф. (1997). «Алгоритм первого прохода для гидродинамического трения и скорости реакции макромолекул, ограниченной диффузией» (PDF). Журнал химической физики. 106 (9): 3761. Bibcode:1997ЖЧФ.106.3761Г. Дои:10.1063/1.473428.
6. Елепов, Б.С.; Михайлов, Г.А. (Январь 1969 г.). «Решение задачи Дирихле для уравнения Δты − у.е. = −q по модели "прогулки по сферам"". Вычислительная математика и математическая физика СССР. 9 (3): 194–204. Дои:10.1016/0041-5553(69)90070-6.
7. Бут, Томас Э (февраль 1981 г.). «Точное решение Монте-Карло эллиптических уравнений в частных производных». Журнал вычислительной физики. 39 (2): 396–404. Bibcode:1981JCoPh..39..396B. Дои:10.1016/0021-9991(81)90159-5.
8. Хван, Чи-Ок; Масканьи, Майкл; Учитывая, Джеймс А. (март 2003 г.). "Реализация интеграла по путям Фейнмана – Каца для уравнения Пуассона с использованием час-обусловленная функция Грина ». Математика и компьютеры в моделировании. 62 (3–6): 347–355. CiteSeerX  10.1.1.123.3156. Дои:10.1016 / S0378-4754 (02) 00224-0.
9. Гобет, Эммануэль (2013). Méthodes de Monte-Carlo et processus stochastiques du linéaire au non-lineaire. Palaiseau: Editions de l'Ecole polytechnique. ISBN  978-2-7302-1616-6.
10. Салминен, Андрей Н. Бородин; Пааво (2002). Справочник по броуновскому движению: факты и формулы (2-е изд.). Базель [u.a.]: Birkhäuser. ISBN  978-3-7643-6705-3.
11. Бут, Томас (август 1982). "Региональное решение методом Монте-Карло эллиптических уравнений в частных производных" (PDF). Журнал вычислительной физики. 47 (2): 281–290. Bibcode:1982JCoPh..47..281B. Дои:10.1016/0021-9991(82)90079-1.
12. Дьякону, Мадалина; Херрманн, Самуэль (декабрь 2013 г.). «Время срабатывания для процессов Бесселя - алгоритм ходьбы по движущимся сферам (WoMS)». Анналы прикладной теории вероятностей. 23 (6): 2259–2289. arXiv:1111.3736. Дои:10.1214 / 12-AAP900.
13. Симонов, Николай А. (2007). Случайные блуждания для решения краевых задач с условиями потока. Численные методы и приложения. Конспект лекций по информатике. 4310. С. 181–188. CiteSeerX  10.1.1.63.3780. Дои:10.1007/978-3-540-70942-8_21. ISBN  978-3-540-70940-4.

дальнейшее чтение

• Сабельфельд, Карл К. (1991). Методы Монте-Карло в краевых задачах. Берлин [и др.]: Springer-Verlag. ISBN  9783540530015.

внешняя ссылка

• Некоторые непрерывные методы Монте-Карло для задачи Дирихле Статья, в которой Марвин Эдгар Мюллер представил метод.
• Броуновское движение Петера Мёртерса и Юваля Переса. См. Главу 3.3 о гармонической мере, функциях Грина и точках выхода.