Калориметрия - Calorimetry


Калориметрия наука или акт измерения изменений в переменные состояния тела с целью получения теплопередача связанных с изменениями его состояния, например, химические реакции, физические изменения, или же фазовые переходы при указанных ограничениях. Калориметрия выполняется с помощью калориметр. Слово калориметрия происходит от латинского слова калорийность, что означает тепло и греческое слово μέτρον (метрон), что означает мера. Шотландский врач и ученый Джозеф Блэк, который первым распознал различие между высокая температура и температура, считается основоположником калориметрии.[2]
Косвенная калориметрия вычисляет высокая температура что живые организмы производят, измеряя производство углекислый газ и азотные отходы (часто аммиак в водных организмах, или мочевина в земных), или от потребления ими кислород. Лавуазье отметил в 1780 году, что производство тепла можно предсказать по потреблению кислорода таким образом, используя множественная регрессия. В динамический энергетический бюджет теория объясняет, почему эта процедура верна. Тепло, выделяемое живыми организмами, также можно измерить прямая калориметрия, в котором весь организм помещается внутрь калориметра для измерения.
Широко распространенным современным инструментом является дифференциальный сканирующий калориметр, устройство, которое позволяет получать тепловые данные на небольших количествах материала. Он включает в себя нагрев образца с контролируемой скоростью и регистрацию теплового потока внутрь или от образца.
Классический калориметрический расчет тепла
Случаи с дифференцируемым уравнением состояния однокомпонентного тела
Базовый классический расчет по объему
Калориметрия требует, чтобы эталонный материал, изменяющий температуру, обладал определенными термическими конститутивными свойствами. Классическое правило, признанное Клаузиус и Кельвин, заключается в том, что давление, оказываемое калориметрическим материалом, полностью и быстро определяется исключительно его температурой и объемом; это правило применяется для изменений, не связанных с фазовым переходом, таких как таяние льда. Есть много материалов, которые не соответствуют этому правилу, и для них настоящая формула классической калориметрии не дает адекватного объяснения. Здесь предполагается, что классическое правило выполняется для используемого калориметрического материала, и утверждения математически записываются:
Тепловой отклик калориметрического материала полностью описывается его давлением как значение его конститутивной функции всего объема и температура . Все приращения здесь должны быть очень маленькими. Этот расчет относится к области объема и температуры тела, в которой не происходит фазового перехода и присутствует только одна фаза. Важным предположением здесь является непрерывность отношений собственности. Для фазового перехода необходим другой анализ.
Когда калориметрическое тело получает небольшое приращение тепла с небольшими приращениями, своего объема, и его температуры, приращения тепла, , полученная массой калориметрического материала, определяется выражением
куда
- обозначает скрытую теплоту по отношению к объему калориметрического материала при постоянной контролируемой температуре . Давление окружающей среды на материал инструментально регулируется, чтобы наложить выбранное изменение объема с начальным объемом . Для определения этой скрытой теплоты изменение объема фактически является независимой инструментально изменяемой величиной. Это скрытое тепло не является одним из широко используемых, но представляет теоретический или концептуальный интерес.
- обозначает теплоемкость калориметрического материала при фиксированном постоянном объеме , в то время как давление материала может изменяться свободно, с начальной температурой . Температура изменяется под воздействием подходящей тепловой ванны. Принято писать просто как , или еще короче как . Это скрытое тепло - одно из двух широко используемых.[3][4][5][6][7][8][9]
Скрытая теплота по отношению к объему - это теплота, необходимая для увеличения объема на единицу при постоянной температуре. Можно сказать, что это `` измеряется по изотерме '', и давление, которое оказывает материал, может свободно изменяться в соответствии с его основным законом. . Для данного материала он может иметь положительный или отрицательный знак или, в исключительных случаях, может быть равен нулю, и это может зависеть от температуры, как и для воды около 4 C.[10][11][12][13] Представление о скрытой теплоте по отношению к объему, возможно, впервые было признано Джозеф Блэк в 1762 г.[14] Также используется термин «скрытая теплота расширения».[15] Скрытое тепло по отношению к объему также можно назвать «скрытой энергией по отношению к объему». Для всех этих случаев использования «скрытой теплоты» в более систематической терминологии используется «скрытая теплоемкость».
Теплоемкость при постоянном объеме - это количество тепла, необходимое для увеличения температуры на единицу при постоянном объеме. Можно сказать, что это «измеряется по изохоре», и, опять же, давление, которое оказывает материал, может свободно изменяться. Это всегда имеет положительный знак. Это означает, что для повышения температуры тела без изменения его объема к нему необходимо подводить тепло. Это согласуется с обычным опытом.
Такие количества, как иногда называют «кривыми дифференциалами», потому что они измеряются по кривым в поверхность.
Классическая теория калориметрии постоянного объема (изохорная)
Калориметрия постоянного объема - это калориметрия, выполняемая при постоянном объем. Это предполагает использование калориметр постоянного объема. Теплота по-прежнему измеряется по вышеуказанному принципу калориметрии.
Это означает, что в калориметре соответствующей конструкции, называемом калориметром бомбы, приращение объема можно заставить исчезнуть, . Для калориметрии постоянного объема:
куда
- обозначает приращение в температура и
- обозначает теплоемкость при постоянной громкости.
Классический расчет тепла по давлению
Из приведенного выше правила расчета теплоты по объему следует правило по давлению.[3][7][16][17]
В процессе небольших приращений его давления, и его температуры, приращения тепла, , полученная массой калориметрического материала, определяется выражением
куда
- обозначает скрытую теплоту по отношению к давлению калориметрического материала при постоянной температуре, в то время как объем и давление тела могут свободно изменяться при давлении и температура ;
- обозначает теплоемкость калориметрического материала при постоянном давлении, в то время как температура и объем тела могут свободно изменяться при давлении и температура . Принято писать просто как , или еще короче как .
Новые количества здесь связаны с предыдущими:[3][7][17][18]
куда
- обозначает частная производная из относительно оценивается для
и
- обозначает частную производную от относительно оценивается для .
Скрытая теплота и всегда имеют противоположный знак.[19]
Обычно отношение удельной теплоемкости называют
Калориметрия по изменению фазы, уравнение состояния показывает скачкообразный разрыв
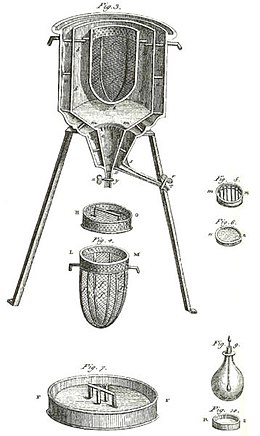
Ранний калориметр использовался Лаплас и Лавуазье, как показано на рисунке выше. Он работал при постоянной температуре и атмосферном давлении. При этом задействованная скрытая теплота не была скрытой теплотой по отношению к объему или по отношению к давлению, как в приведенном выше описании калориметрии без фазового перехода. Скрытая теплота, задействованная в этом калориметре, связана с фазовым переходом, естественным образом происходящим при постоянной температуре. Этот вид калориметра работал путем измерения массы воды, образовавшейся в результате таяния льда, что является изменение фазы.
Накопление тепла
Для зависящего от времени процесса нагрева калориметрического материала, определяемого непрерывным совместным прогрессированием из и , начиная со времени и заканчивается во времени , можно рассчитать накопленное количество отпущенного тепла, . Этот расчет выполняется математическое интегрирование по прогрессии относительно времени. Это потому, что приращения тепла являются «аддитивными»; но это не означает, что тепло - величина консервативная. Идея о том, что тепло - это консервативная величина, была изобретена Лавуазье, и называется 'теория калорий '; к середине XIX века это было признано ошибочным. Написано символом , количество вовсе не ограничивается приращением с очень маленькими значениями; это в отличие от .
Можно написать
- .
В этом выражении используются такие величины, как которые определены в разделе ниже, озаглавленном «Математические аспекты приведенных выше правил».
Математические аспекты приведенных выше правил
Использование «очень малых» количеств, таких как связано с физическими требованиями к количеству быть "быстро определенным" и ; такое «быстрое определение» относится к физическому процессу. Эти «очень маленькие» количества используются в Лейбниц подход к исчисление бесконечно малых. В Ньютон подход вместо этого использует 'флюсии ' Такие как , что делает более очевидным, что должно быть «быстро определено».
В терминах флюксий первое правило расчета выше можно записать[22]
куда
- обозначает время
- обозначает временную скорость нагрева калориметрического материала за время
- обозначает скорость изменения объема калориметрического материала во времени
- обозначает скорость изменения температуры калориметрического материала во времени.
Приращение и текучесть получены за определенное время который определяет значения величин в правых частях приведенных выше правил. Но это не повод ожидать, что должен существовать математическая функция . По этой причине приращение называется "несовершенным дифференциалом" или "неточная разница '.[23][24][25] В некоторых книгах это указывается записью вместо .[26][27] Также обозначение đQ используется в некоторых книгах.[23][28] Невнимательность к этому может привести к ошибке.[29]
Количество правильно сказано, чтобы быть функциональный непрерывного развития суставов из и , но в математическом определении функция, не является функцией . Хотя текучесть здесь определяется как функция времени , символы и соответственно отдельно стоящие не определены.
Физические рамки приведенных выше правил калориметрии
Приведенные выше правила относятся только к подходящим калориметрическим материалам. Термины «быстро» и «очень мало» требуют эмпирической физической проверки области применимости вышеуказанных правил.
Приведенные выше правила расчета теплоты относятся к чистой калориметрии. Они не ссылаются на термодинамика, и были в основном поняты до появления термодинамики. Они составляют основу «термо» вклада в термодинамику. Вклад «динамики» основан на идее работай, который не используется в приведенных выше правилах расчета.
Экспериментально удобно измеряемые коэффициенты
Эмпирически удобно измерять свойства калориметрических материалов в экспериментально контролируемых условиях.
Повышение давления при постоянном объеме
Для измерений в экспериментально контролируемом объеме можно использовать высказанное выше предположение о том, что давление тела калориметрического материала может быть выражено как функция его объема и температуры.
Для измерения при постоянном экспериментально контролируемом объеме изохорный коэффициент роста давления с температурой определяется как
- .[30]
Расширение при постоянном давлении
Для измерений при экспериментально контролируемом давлении предполагается, что объем тела калориметрического материала можно выразить как функцию его температуры и давление . Это предположение связано, но не то же самое, что и использованное выше предположение о том, что давление тела калориметрического материала известно как функция его объема и температуры; аномальное поведение материалов может повлиять на это соотношение.
Величина, которую удобно измерять при постоянном экспериментально контролируемом давлении, коэффициент изобарного объемного расширения, определяется как
Сжимаемость при постоянной температуре
Для измерений при экспериментально контролируемой температуре снова предполагается, что объем тела калориметрического материала можно выразить как функцию его температуры и давление , с теми же оговорками, что и упомянутые выше.
Величина, которую удобно измерять при постоянной экспериментально контролируемой температуре, изотермическая сжимаемость, определяется как
Связь классических калориметрических величин
Предполагая, что правило известно, можно получить функцию который используется выше в классическом расчете тепла по отношению к давлению. Эту функцию можно найти экспериментально из коэффициентов и через математически выводимое соотношение
- .[37]
Связь калориметрии и термодинамики
Термодинамика Постепенно развивался в течение первой половины девятнадцатого века, основываясь на вышеупомянутой теории калориметрии, которая была разработана до нее, и на других открытиях. Согласно Гисласону и Крейгу (2005): «Большинство термодинамических данных поступает из калориметрии ...»[38] Согласно Кондепуди (2008): «Калориметрия широко используется в современных лабораториях».[39]
С точки зрения термодинамики внутренняя энергия калориметрического материала можно рассматривать как значение функции из , с частными производными и .
Тогда можно показать, что можно написать термодинамическую версию вышеуказанных калориметрических правил:
с
и
Опять же, что касается термодинамики, внутренняя энергия калориметрического материала может иногда, в зависимости от калориметрического материала, рассматриваться как значение функции из , с частными производными и , и с выражается как значение функции из , с частными производными и .
Затем, согласно Адкинсу (1975),[44] можно показать, что можно написать еще одну термодинамическую версию приведенных выше калориметрических правил:
с
и
- .[44]
Помимо калориметрического факта, отмеченного выше, скрытая теплота и всегда имеют противоположный знак, можно показать, используя термодинамическую концепцию работы, что также
Особый интерес термодинамики в калориметрии: изотермические сегменты цикла Карно
Калориметрия имеет особое преимущество в термодинамике. Он говорит о тепле, поглощенном или выделяемом в изотермическом сегменте Цикл Карно.
Цикл Карно - это особый вид циклического процесса, воздействующего на тело, состоящее из материала, пригодного для использования в тепловом двигателе. Такой материал относится к тому типу, который рассматривается в калориметрии, как отмечалось выше, который оказывает давление, которое очень быстро определяется только температурой и объемом. Говорят, что такое тело изменяется обратимо. Цикл Карно состоит из четырех последовательных этапов или сегментов:
(1) изменение громкости по сравнению с объемом к тому при постоянной температуре чтобы вызвать поток тепла в тело (известный как изотермическое изменение)
(2) изменение громкости с к тому при переменной температуре, чтобы не было потока тепла (известное как адиабатическое изменение)
(3) еще одно изотермическое изменение объема от к тому при постоянной температуре например, чтобы вызвать поток или тепло из тела и точно подготовиться к следующему изменению
(4) еще одно адиабатическое изменение объема от вернуться к просто чтобы вернуть тело к исходной температуре .
На изотермическом участке (1) тепло, поступающее в тело, определяется выражением
а в изотермическом сегменте (3) тепло, выходящее из тела, определяется выражением
- .[46]
Поскольку сегменты (2) и (4) являются адиабатами, во время их работы тепло не течет внутрь или из тела, и, следовательно, чистое тепло, подводимое к телу во время цикла, определяется выражением
- .
Эта величина используется термодинамикой и особым образом связана с сетью работай совершается телом во время цикла Карно. Чистое изменение внутренней энергии тела во время цикла Карно, , равняется нулю, поскольку материал рабочего тела имеет указанные выше особые свойства.
Особый интерес калориметрии в термодинамике: соотношения между классическими калориметрическими величинами
Связь скрытой теплоты с объемом и уравнение состояния
Количество , скрытая теплота по отношению к объему, относится к классической калориметрии. Он объясняет возникновение передачи энергии работой в процессе, в котором также передается тепло; количество, однако, было рассмотрено до того, как связь между теплопередачей и работой была прояснена изобретением термодинамики. В свете термодинамики обнаруживается, что классическая калориметрическая величина тесно связана с уравнением состояния калориметрического материала. . При условии, что температура измеряется в термодинамической абсолютной шкале, соотношение выражается формулой
- .[47]
Разница удельных плавок
Расширенная термодинамика обеспечивает соотношение
- .
Отсюда дальнейшие математические и термодинамические рассуждения приводят к другому соотношению между классическими калориметрическими величинами. Разница удельных плавок выражается как
Практическая калориметрия постоянного объема (калориметрия бомбы) для термодинамических исследований
Калориметрия постоянного объема - это калориметрия, выполняемая при постоянном объем. Это предполагает использование калориметр постоянного объема.
В калориметрии постоянного объема работа не выполняется, поэтому измеренное количество тепла равно изменению внутренней энергии системы. Предполагается, что теплоемкость при постоянном объеме не зависит от температуры.
Теплота измеряется по принципу калориметрии.
куда
- ΔU это изменение в внутренняя энергия,
- ΔТ это изменение в температура и
- CV это теплоемкость при постоянной громкости.
В калориметрия постоянного объема то давление не считается постоянной. Если существует разница давлений между начальным и конечным состояниями, измеренное количество тепла требует корректировки, чтобы обеспечить энтальпия изменять. Тогда есть
куда
- ΔЧАС это изменение в энтальпия и
- V - неизменный объем камеры для образца.
Смотрите также
- Изотермическая микрокалориметрия (ИМК)
- Изотермическая калориметрия титрования
- Сорбционная калориметрия
- Калориметр реакции
Рекомендации
- ^ Рирдон, Фрэнсис Д .; Leppik, Kalle E .; Вегманн, Рене; Уэбб, Пол; Ducharme, Miche B .; И Кенни, Глен П. (2006). Человеческий калориметр Снеллена пересмотрен, модернизирован и модернизирован: дизайн и рабочие характеристики. Med Bio Eng Comput, 44:721–728.
- ^ Лайдлер, Кейт, Дж. (1993). Мир физической химии. Издательство Оксфордского университета. ISBN 0-19-855919-4.
- ^ а б c Брайан, Г. (1907), страницы 21–22.
- ^ Партингтон, Дж. Р. (1949), страницы 155–157.
- ^ Пригожин И., Дефай Р. (1950/1954). Химическая термодинамика, Longmans, Green & Co, Лондон, страницы 22–23.
- ^ Кроуфорд, Ф.Х. (1963), Раздел 5.9, стр. 120–121.
- ^ а б c Адкинс, C.J. (1975), раздел 3.6, страницы 43-46.
- ^ Трусделл, К., Бхарата, С. (1977), страницы 20-21.
- ^ Ландсберг, П. (1978), стр.11.
- ^ Максвелл, Дж. К. (1872), страницы 232-233.
- ^ Льюис, Г.Н., Рэндалл, М. (1923/1961), страницы 378-379.
- ^ Truesdell, C., Bharatha, S. (1977), страницы 9-10, 15-18, 36-37.
- ^ Трусделл, К.А. (1980). Трагикомическая история термодинамики 1822–1854 гг., Спрингер, Нью-Йорк, ISBN 0-387-90403-4.
- ^ Льюис, Г.Н., Рэндалл, М. (1923/1961), стр.29.
- ^ Максвелл, Дж. К. (1872 г.), стр. 73.
- ^ Кроуфорд, Ф.Х. (1963), Раздел 5.10, стр. 121–122.
- ^ а б Трусделл, К., Бхарата, С. (1977), стр. 23.
- ^ Кроуфорд, Ф.Х. (1963), Раздел 5.11, стр. 123–124.
- ^ Трусделл, К., Бхарата, С. (1977), стр. 24.
- ^ Трусделл, К., Бхарата, С. (1977), стр.25.
- ^ Кондепуди, Д. (2008), страницы 66-67.
- ^ Трусделл, К., Бхарата, С. (1977), стр.20.
- ^ а б Адкинс, К.Дж. (1975), раздел 1.9.3, стр. 16.
- ^ Ландсберг, П. (1978), страницы 8-9.
- ^ Отчет об этом дан Landsberg, P.T. (1978), Глава 4, страницы 26-33.
- ^ Фаулер, Р., Гуггенхайм, Э.А. (1939/1965). Статистическая термодинамика. Версия статистической механики для студентов-физиков и химиков, Cambridge University Press, Кембридж, Великобритания, стр. 57.
- ^ Гуггенхайм, Э.А. (1949/1967), Раздел 1.10, страницы 9-11.
- ^ Лебон, Г., Джоу, Д., Касас-Васкес, Дж. (2008). Понимание неравновесной термодинамики: основы, приложения, границы, Springer-Verlag, Берлин, ISBN 978-3-540-74252-4, стр.7.
- ^ а б Планк, М. (1923/1926), стр. 57.
- ^ а б Ирибарн, Дж. В., Годсон, В. Л. (1973/1981), стр. 46.
- ^ а б c Льюис, Г.Н., Рэндалл, М. (1923/1961), стр. 54.
- ^ а б Гуггенхайм, Э.А. (1949/1967), стр. 38.
- ^ а б Каллен, Х. (1960/1985), стр. 84.
- ^ а б Адкинс, К.Дж. (1975), стр. 38.
- ^ а б Байлин М. (1994), стр. 49.
- ^ а б Кондепуди, Д. (2008), стр.180.
- ^ а б Кондепуди, Д. (2008), стр.181.
- ^ Гисласон, Э.А., Крейг, Северная Каролина (2005). Укрепление основ термодинамики: сравнение основанных на системе и окружающей среде определений работы и тепла, J. Chem. Термодинамика 37: 954-966.
- ^ Кондепуди, Д. (2008), стр.
- ^ Престон, Т. (1894/1904). Теория тепла, второе издание, отредактированное Дж. Р. Коттером, Макмиллан, Лондон, страницы 700-701.
- ^ Адкинс, С.Дж. (1975), стр. 45.
- ^ Трусделл, К., Бхарата, С. (1977), стр. 134.
- ^ Кондепуди, Д. (2008), стр. 64.
- ^ а б Адкинс, К.Дж. (1975), стр. 46.
- ^ Трусделл, К., Бхарата, С. (1977), стр. 59.
- ^ Трусделл, К., Бхарата, С. (1977), страницы 52-53.
- ^ Трусделл, К., Бхарата, С. (1977), стр. 150.
- ^ Каллен, Х. (1960/1985), стр. 86.
Книги
- Адкинс, К.Дж. (1975). Равновесная термодинамика, второе издание, McGraw-Hill, Лондон, ISBN 0-07-084057-1.
- Байлын, М. (1994). Обзор термодинамики, Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3.
- Брайан, Г. (1907). Термодинамика. Вводный трактат, посвященный главным образом Первым принципам и их прямым приложениям, Б.Г. Тюбнер, Лейпциг.
- Каллен, Х. (1960/1985). Термодинамика и введение в термостатистику, второе издание, Wiley, New York, ISBN 981-253-185-8.
- Кроуфорд, F.H. (1963). Тепло, термодинамика и статистическая физика, Руперт Харт-Дэвис, Лондон, Harcourt, Brace, & World.
- Гуггенхайм, Э.А. (1949/1967). Термодинамика. Передовое лечение для химиков и физиков, Северная Голландия, Амстердам.
- Ирибарн, Дж. В., Годсон, В. Л. (1973/1981), Атмосферная термодинамика, второе издание, D. Reidel, Kluwer Academic Publishers, Dordrecht, ISBN 90-277-1296-4.
- Кондепуди, Д. (2008). Введение в современную термодинамику, Уайли, Чичестер, ISBN 978-0-470-01598-8.
- Ландсберг, П. (1978). Термодинамика и статистическая механика, Oxford University Press, Оксфорд, ISBN 0-19-851142-6.
- Льюис, Г.Н., Рэндалл, М. (1923/1961). Термодинамика, второе издание отредактировано К.С. Питцером, Л. Брюером, МакГроу-Хилл, Нью-Йорк.
- Максвелл, Дж. К. (1872 г.). Теория тепла, третье издание, Longmans, Green, and Co., Лондон.
- Партингтон, Дж. Р. (1949). Расширенный трактат по физической химии, Том 1, Основные принципы. Свойства газов, Longmans, Green, and Co., Лондон.
- Планк, М. (1923/1926). Трактат по термодинамике, третье английское издание, переведенное А. Оггом из седьмого немецкого издания, Longmans, Green & Co., Лондон.
- Трусделл, К., Бхарата, С. (1977). Концепции и логика классической термодинамики как теории тепловых двигателей, строго построенные на фундаменте, заложенном С. Карно и Ф. Ричем, Спрингер, Нью-Йорк, ISBN 0-387-07971-8.





























































![delta Q = left [p (V, T), +, left.frac {частичный U} {частичный V} ight | _ {(V, T)} ight], delta V, +, left.frac {частичный U} {partial T} ight | _ {(V, T)}, дельта T](https://wikimedia.org/api/rest_v1/media/math/render/svg/f84955a4832939c4d1337fcfadae0affc3a945bc)








![дельта Q = влево [влево. frac {partial U} {partial p} ight | _ {(p, T)}, +, p left.frac {partial V} {partial p} ight | _ {(p, T)} ight] delta p, + , left [left.frac {частичный U} {частичный T} полет | _ {(p, T)}, +, p left.frac {частичный V} {частичный T} полет | _ {(p, T)} полет ] дельта Т](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80e88197ed385fd3debc25941f418cec98cd244)















![C_p (p, T) -C_V (V, T) = left [p (V, T), +, left.frac {частичный U} {частичный V} полет | _ {(V, T)} полет], left .frac {partial V} {partial T} ight | _ {(p, T)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e5046f626f9dccc1569d9c418d77d6cd6c0a06b)


