Центроидальная мозаика Вороного - Centroidal Voronoi tessellation


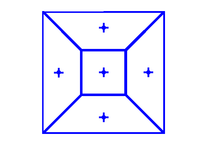
В геометрия, а центроидная мозаика Вороного (CVT) это особый тип тесселяции Вороного или Диаграмма Вороного. Тесселяция Вороного называется центроидальной, если порождающая точка каждой ячейки Вороного также является ее центроид, то есть среднее арифметическое или центр масс. Его можно рассматривать как оптимальное разбиение, соответствующее оптимальному распределению генераторов. Для создания центроидных мозаик Вороного можно использовать ряд алгоритмов, включая Алгоритм Ллойда за К-средство кластеризации или Квазиньютоновские методы подобно BFGS.[1]
Доказательства
Гипотеза Гершо, доказанная для одного и двух измерений, гласит, что «асимптотически говоря, все ячейки оптимального CVT, образуя мозаика, находятся конгруэнтный в базовую ячейку, которая зависит от размера ".[2]
В двух измерениях основная ячейка для оптимального вариатора - это обычный шестиугольник как оказалось, самый плотный упаковка кругов в двухмерном евклидовом пространстве. Его трехмерным эквивалентом является ромбические додекаэдрические соты, полученный из наиболее плотных упаковка сфер в трехмерном евклидовом пространстве.
Приложения
Центроидальные мозаики Вороного полезны в Сжатие данных, оптимальный квадратура, оптимальный квантование, кластеризация, и оптимальное создание сетки.[3]
Взвешенная центроидная диаграмма Вороного - это вариатор, в котором каждый центроид взвешивается в соответствии с определенной функцией. Например, оттенки серого изображение может использоваться как функция плотности для взвешивания точек вариатора, как способ создания цифровых штриховка.[4]
Встречаемость в природе
Много узоры в природе хорошо аппроксимируются центроидальной мозаикой Вороного. Примеры этого включают Дорога гигантов, клетки роговица,[5] и гнездовые ямы самца тилапия.[3]
Рекомендации
- ^ Нокедаль, Хорхе; Райт, Стивен Дж. (2006). Численная оптимизация (второе изд.). Springer. Дои:10.1007/978-0-387-40065-5.
- ^ Ду, Цян; Ван, Дешенг (2005), "Оптимальные центроидные мозаики Вороного и гипотеза Гершо в трехмерном пространстве", Компьютеры и математика с приложениями (49): 1355–1373
- ^ а б Ду, Цян; Фабер, Вэнс; Гунцбургер, Макс (1999), "Центроидальные мозаики Вороного: приложения и алгоритмы", SIAM Обзор, 41 (4): 637–676, CiteSeerX 10.1.1.452.2448, Дои:10.1137 / S0036144599352836.
- ^ Секорд, Адриан. "Утяжеленная вороной пунктирная линия". Материалы 2-го международного симпозиума по нефотореалистичной анимации и рендерингу. ACM, 2002.
- ^ Пигатто, Жоао Антонио Тадеу; и другие. (2009). «Сканирующая электронная микроскопия эндотелия роговицы страуса». Cienc. Деревенский. 39 (3): 926–929. Дои:10.1590 / S0103-84782009005000001.
