Сравнительная статика - Comparative statics
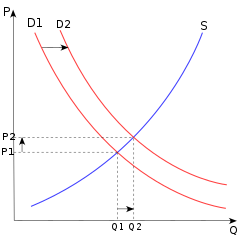
В экономика, сравнительная статика представляет собой сравнение двух различных экономических результатов до и после изменения некоторых основных экзогенный параметр.[1]
Как вид статический анализ он сравнивает два разных равновесие состояния, после процесса настройки (если есть). Он не изучает ни движение к равновесию, ни сам процесс изменения.
Сравнительная статика обычно используется для изучения изменений в спрос и предложение при анализе сингла рынок, и изучить изменения в денежный или же фискальная политика при анализе всего экономия. Сравнительная статика - инструмент анализа в микроэкономика (включая общее равновесие анализ) и макроэкономика. Сравнительная статика формализована Джон Р. Хикс (1939) и Пол А. Самуэльсон (1947) (Кехо, 1987, стр. 517), но был представлен графически, по крайней мере, с 1870-х годов.[2]
Для моделей стабильных равновесных скоростей изменения, таких как неоклассическая модель роста, сравнительная динамика является аналогом сравнительной статики (Eatwell, 1987).
Линейное приближение
Результаты сравнительной статики обычно получают с помощью теорема о неявной функции рассчитать линейное приближение к системе уравнений, определяющей равновесие, в предположении, что равновесие устойчиво. То есть, если мы рассмотрим достаточно небольшое изменение какого-либо экзогенного параметра, мы можем рассчитать, как изменяется каждая эндогенная переменная, используя только первые производные членов, входящих в уравнения равновесия.
Например, предположим, что равновесное значение некоторой эндогенной переменной определяется следующим уравнением:
куда - экзогенный параметр. Тогда в первом приближении изменение вызвано небольшим изменением в должен удовлетворять:
Здесь и представляют изменения в и соответственно, а и частные производные от относительно и (оценивается при начальных значениях и ), соответственно. Точно так же мы можем записать изменение в в качестве:
Разделив последнее уравнение на dа дает сравнительная статическая производная из Икс относительно а, также называемый множитель из а на Икс:
Многие уравнения и неизвестные
Все приведенные выше уравнения остаются верными в случае системы уравнения в неизвестные. Другими словами, предположим представляет собой систему уравнения, содержащие вектор неизвестные , а вектор данные параметры . Если мы сделаем достаточно небольшое изменение в параметрах, то результирующие изменения эндогенных переменных можно сколь угодно хорошо аппроксимировать с помощью . В этом случае, представляет × матрица частных производных функций по переменным , и представляет × матрица частных производных функций по параметрам . (Производные в и оцениваются при начальных значениях и .) Обратите внимание, что если кто-то хочет просто сравнительного статического воздействия одной экзогенной переменной на одну эндогенную переменную, Правило Крамера можно использовать на полностью дифференцированный система уравнений .
Стабильность
Предположение, что равновесие является устойчивым, имеет значение по двум причинам. Во-первых, если равновесие было нестабильным, небольшое изменение параметра могло бы вызвать большой скачок значения , делая недействительным использование линейного приближения. Более того, Пол А. Самуэльсон с принцип соответствия[3][4][5]:С. 122–123. утверждает, что стабильность равновесия имеет качественное значение относительно сравнительных статических эффектов. Другими словами, знание того, что равновесие устойчиво, может помочь нам предсказать, будет ли каждый из коэффициентов в векторе положительный или отрицательный. В частности, один из п необходимым и совместно достаточным условием устойчивости является то, что детерминант из п×п матрица B иметь определенный знак; поскольку этот определитель появляется как знаменатель в выражении для , знак определителя влияет на знаки всех элементов вектора сравнительных статических эффектов.
Пример роли предположения об устойчивости
Предположим, что объемы спроса и предложения продукта определяются следующими уравнениями:
куда это объем спроса, поставляемое количество, п это цена, а и c являются параметрами-перехватчиками, определяемыми внешними воздействиями на спрос и предложение соответственно, б <0 - величина, обратная наклону кривая спроса, и грамм - величина, обратная наклону кривой предложения; грамм > 0, если кривая предложения имеет восходящий наклон, грамм = 0, если кривая предложения вертикальная, и грамм <0, если кривая предложения изгибается назад. Если мы приравняем количество предложения к количеству спроса, чтобы найти равновесную цену , мы находим, что
Это означает, что равновесная цена положительно зависит от точки пересечения спроса, если грамм – б > 0, но отрицательно зависит от него, если грамм – б <0. Какая из этих возможностей актуальна? Фактически, начиная с начального статического равновесия и затем меняя а, новое равновесие актуально Только если рынок действительно перейдет к этому новому равновесию. Предположим, что ценовые корректировки на рынке происходят в соответствии с
куда > 0 - параметр скорости настройки и это производная по времени цены - то есть показывает, насколько быстро и в каком направлении цена меняется. К теория устойчивости, п будет сходиться к своему равновесному значению тогда и только тогда, когда производная отрицательный. Эта производная дается формулой
Это отрицательно тогда и только тогда, когда грамм – б > 0, и в этом случае параметр перехвата спроса а положительно влияет на цену. Таким образом, мы можем сказать, что, хотя направление воздействия ограничения спроса на равновесную цену неоднозначно, когда все, что мы знаем, это то, что обратная величина наклона кривой предложения, грамм, является отрицательным, в единственном значимом случае (когда цена фактически достигает своего нового равновесного значения) увеличение точки пересечения спроса увеличивает цену. Обратите внимание, что в этом случае с грамм – б > 0 - это случай, когда кривая предложения, если она имеет отрицательный наклон, круче кривой спроса.
Без ограничений
Предполагать - гладкая и строго вогнутая целевая функция, где Икс вектор п эндогенные переменные и q вектор м экзогенные параметры. Рассмотрим задачу безусловной оптимизации .Позволять , то п к п матрица первых частных производных от относительно своего первого п аргументы Икс1,...,Иксп.Максимайзер определяется п× 1 условие первого порядка .
Сравнительная статика спрашивает, как этот максимайзер изменяется в ответ на изменения в м параметры. Цель - найти .
Строгая вогнутость целевой функции означает, что якобиан ж, которая в точности является матрицей вторых частных производных от п по отношению к эндогенным переменным неособен (имеет обратный). Посредством теорема о неявной функции, тогда, можно рассматривать локально как непрерывно дифференцируемую функцию, а локальный отклик к небольшим изменениям в q дан кем-то
Применяя цепное правило и условие первого порядка,
(Видеть Теорема о конверте ).
Приложение для максимизации прибыли
Предположим, фирма производит п товары в количествах . Прибыль фирмы - это функция п из и из м экзогенные параметры которые могут представлять собой, например, различные налоговые ставки. При условии, что функция прибыли удовлетворяет требованиям гладкости и вогнутости, метод сравнительной статики, описанный выше, описывает изменения в прибыли фирмы из-за небольших изменений налоговых ставок.
С ограничениями
Обобщение описанного выше метода позволяет включить в задачу оптимизации набор ограничений. Это приводит к общему теорема о конверте. Приложения включают определение изменений в Маршаллианский спрос в ответ на изменение цены или заработной платы.
Ограничения и расширения
Одним из ограничений сравнительной статики, использующей теорему о неявной функции, является то, что результаты действительны только в (потенциально очень малой) окрестности оптимума, то есть только для очень небольших изменений экзогенных переменных. Еще одно ограничение - потенциально чрезмерно ограничительный характер допущений, обычно используемых для обоснования процедур сравнительной статики. Например, Джон Накбар в одном из своих тематических исследований обнаружил, что использование сравнительной статики в анализе общего равновесия лучше всего работает с очень небольшими индивидуальными данными, а не на агрегированном уровне.[6]
Пол Милгром и Крис Шеннон[7] указал в 1994 году, что предположения, традиционно используемые для обоснования использования сравнительной статики в задачах оптимизации, на самом деле не нужны - в частности, предположения о выпуклости предпочтительных наборов или наборов ограничений, гладкости их границ, условий первой и второй производных и линейности бюджетных наборов или целевых функций. Фактически, иногда задача, удовлетворяющая этим условиям, может быть монотонно преобразована в задачу с идентичной сравнительной статикой, но с нарушением некоторых или всех этих условий; следовательно, эти условия не являются необходимыми для обоснования сравнительной статики. Исходя из статьи Милгрома и Шеннона, а также результатов, полученных Вейноттом.[8] и Топкис[9] важная часть исследование операций был разработан под названием монотонная сравнительная статика. В частности, эта теория концентрируется на сравнительном статическом анализе с использованием только условий, которые не зависят от преобразований, сохраняющих порядок. Метод использует теория решетки и вводит понятия квазисверхмодулярности и условия однократного пересечения. Широкое применение монотонной сравнительной статики в экономике включает теорию производства, теорию потребителей, теорию игр с полной и неполной информацией, теорию аукционов и другие.[10]
Смотрите также
Примечания
- ^ (Мас-Колелл, Уинстон и Грин, 1995, с. 24; Зильберберг и Суен, 2000)
- ^ Флиминг Дженкин (1870 г.), «Графическое представление законов спроса и предложения и их применение к труду», у Александра Гранта, Исследования в перерывах и (1872 г.), «О принципах, регулирующих налогообложение», Труды Королевского общества Эдинбурга 1871-22 гг., стр. 618-30., Также в Статьи, литературные, научные и т. Д., т. 2 (1887), изд. С.К. Колвин, Дж. А. Ewing с помощью прокрутки к главе ссылки.
- ^ Самуэльсон, Пол, "Устойчивость равновесия: сравнительная статика и динамика", Econometrica 9, April 1941, 97-120: вводит понятие принципа соответствия.
- ^ Самуэльсон, Пол, "Устойчивость равновесия: линейные и нелинейные системы", Econometrica 10 (1) января 1942, 1-25: вводит термин «принцип соответствия».
- ^ Баумоль, Уильям Дж., Экономическая динамика, Macmillan Co., 3-е издание, 1970 г.
- ^ "U-M Weblogin". weblogin.umich.edu. Дои:10.1057/978-1-349-95121-5_322-2. Получено 2020-12-02.
- ^ Милгром, Пол, и Шеннон, Крис. «Монотонная сравнительная статика» (1994). Econometrica, Vol. 62 Выпуск 1, стр. 157-180.
- ^ Вейнотт (1992): Программирование на решетке: качественная оптимизация и равновесия. MS Stanford.
- ^ См .: Топкис Д. М. (1979): «Точки равновесия в субмодульных играх с ненулевой суммой n человек», SIAM Journal of Control and Optimization, 17, 773–787; а также Topkis, D. M. (1998): Supermodularity and Complementarity, Frontiers of Economic Research, Princeton University Press, ISBN 9780691032443.
- ^ См .: Topkis, D. M. (1998): Supermodularity and Complementarity, Frontiers of Economic Research, Princeton University Press, ISBN 9780691032443; и Вивес, X. (2001): Ценообразование олигополии: старые идеи и новые инструменты. MIT Press, ISBN 9780262720403.
Рекомендации
- Джон Итуэлл и др., Изд. (1987). «Сравнительная динамика», В New Palgrave: экономический словарь, т. 1, с. 517.
- Джон Р. Хикс (1939). Стоимость и капитал.
- Тимоти Дж. Кехо, 1987. «Сравнительная статика», Новый Пэлгрейв: экономический словарь, т. 1, стр. 517–20.
- Андреу Мас-Колелл, Майкл Д. Уинстон и Джерри Р. Грин, 1995. Микроэкономическая теория.
- Пол А. Самуэльсон (1947). Основы экономического анализа.
- Юджин Зильберберг и Винг Суен, 2000. Структура экономики: математический анализ, 3-е изд.





































![D_ {q} x ^ {*} (q) = - [D_ {x} f (x ^ {*} (q); q)] ^ {{- 1}} D_ {q} f (x ^ {* } (q); q).](https://wikimedia.org/api/rest_v1/media/math/render/svg/e89de8f875adb74f0fc6993538f4a093db09d6f4)


