Конус (теория категорий) - Cone (category theory)
В теория категорий, филиал математика, то конус функтора это абстрактное понятие, используемое для определения предел того, что функтор. В теории категорий конусы появляются и в других случаях.
Определение
Позволять F : J → C быть диаграмма в C. Формально диаграмма - это не более чем функтор от J к C. Изменение терминологии отражает тот факт, что мы думаем о F как индексирование семьи объекты и морфизмы в C. В категория J считается "индексной категорией". Это следует рассматривать по аналогии с понятием индексированная семья объектов в теория множеств. Основное отличие состоит в том, что здесь тоже есть морфизмы. Так, например, когда J это дискретная категория, это наиболее близко соответствует идее индексированного семейства в теории множеств. Другой распространенный и более интересный пример берет J быть размах. J также можно принять за пустую категорию, ведущую к простейшим конусам.
Позволять N быть объектом C. А конус от N к F семейство морфизмов
для каждого объекта Икс из J, такая, что для каждого морфизма ж : Икс → Y в J следующая диаграмма ездит на работу:

Совокупность (обычно бесконечная) всех этих треугольников можно (частично) изобразить в виде конус с вершиной N. Иногда говорят, что конус ψ имеет вершина N и база F.
Также можно определить двойной понятие конус от F к N (также называемый конус), перевернув все стрелки вверху. Явно конус из F к N семейство морфизмов
для каждого объекта Икс из J, такая, что для каждого морфизма ж : Икс → Y в J следующая диаграмма коммутирует:

Эквивалентные составы
На первый взгляд конусы кажутся слегка ненормальными конструкциями в теории категорий. Это карты из объект к функтор (или наоборот). В соответствии с духом теории категорий мы хотели бы определить их как морфизмы или объекты в некоторой подходящей категории. Фактически, мы можем сделать и то, и другое.
Позволять J быть небольшой категорией и пусть CJ быть категория диаграмм типа J в C (это не более чем категория функторов ). Определить диагональный функтор Δ: C → CJ следующим образом: Δ (N) : J → C это постоянный функтор к N для всех N в C.
Если F диаграмма типа J в C, следующие утверждения эквивалентны:
- ψ - конус из N к F
- ψ - это естественная трансформация из Δ (N) к F
- (N, ψ) - объект в категория запятой (Δ ↓ F)
Двойные утверждения также эквивалентны:
- ψ - конус из F к N
- ψ - это естественная трансформация от F к Δ (N)
- (N, ψ) - объект в категория запятой (F ↓ Δ)
Все эти утверждения могут быть проверены прямым применением определений. Думая о колбочках как о естественных преобразованиях, мы видим, что это просто морфизмы в CJ с источником (или целью) константный функтор.
Категория шишек
Согласно вышеизложенному, мы можем определить категория шишек F как категория запятой (Δ ↓ F). Тогда морфизмы конусов будут просто морфизмами в этой категории. Эта эквивалентность коренится в наблюдении, что естественное отображение между постоянными функторами Δ (N), Δ (M) соответствует морфизму между N и M. В этом смысле диагональный функтор действует на стрелки тривиально. Аналогичным образом, записывая определение естественного отображения от постоянного функтора Δ (N) к F дает ту же диаграмму, что и выше. Как и следовало ожидать, морфизм из конуса (N, ψ) в конус (L, φ) - это просто морфизм N → L так что все "очевидные" диаграммы коммутируют (см. первую диаграмму в следующем разделе).
Точно так же категория со-конусов из F категория запятой (F ↓ Δ).
Универсальные конусы
Пределы и коллимиты определены как универсальные конусы. То есть конусы, через которые действуют все остальные колбочки. Конус φ из L к F является универсальным конусом, если для любого другого конуса ψ из N к F существует единственный морфизм из ψ в φ.
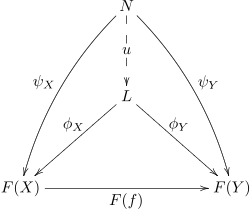
Эквивалентно универсальный конус для F это универсальный морфизм от Δ до F (мыслится как объект в CJ) или конечный объект в (Δ ↓F).
Двойственно конус φ из F к L является универсальным конусом, если для любого другого конуса ψ из F к N существует единственный морфизм от φ к ψ.

Эквивалентно универсальный конус из F универсальный морфизм из F к Δ, или исходный объект в (F ↓ Δ).
Предел F универсальный конус для F, а копредел - универсальный конус из F. Как и в случае со всеми универсальными конструкциями, наличие универсальных конусов не гарантируется для всех диаграмм. F, но если они существуют, то единственны с точностью до единственного изоморфизма (в категории запятой (∆ ↓F)).
использованная литература
- Мак-Лейн, Сондерс (1998). Категории для рабочего математика (2-е изд.). Нью-Йорк: Спрингер. ISBN 0-387-98403-8.
- Борсё, Фрэнсис (1994). «Пределы». Справочник по категориальной алгебре. Энциклопедия математики и ее приложений 50-51, 53 [т.е. 52]. Том 1. Издательство Кембриджского университета. ISBN 0-521-44178-1.


