Динамика полета (КА) - Flight dynamics (spacecraft)

Эта статья о динамике полета космического корабля. О динамике полета самолета см. Динамика полета (самолет). Для управления ориентацией космического корабля см. Контроль отношения.

Траектория полета Аполлон-11 посадка человека на Луну, июль 1969 г.

Динамика полета космического корабля это применение механическая динамика к модель как внешние силы, действующие на космический аппарат или же космический корабль определить траекторию его полета. Эти силы в основном бывают трех типов: движущий сила, создаваемая двигателями автомобиля; гравитационный сила со стороны Земли и других небесных тел; и аэродинамическая подъемная сила и сопротивление (при полете в атмосфера Земли или другое тело, такое как Марс или Венера).

На основе принципов динамики полета моделируется орбитальный полет космического корабля; маневры по изменению орбиты; транслунный и межпланетный полет; полет транспортного средства при запуске с Земли или запуск и посадка космического корабля на небесное тело с атмосферой или без нее; вход через атмосферу Земли или другого небесного тела; и контроль отношения. Обычно они программируются в автомобиле инерциальные навигационные системы, и под наблюдением на местах членом полетный контроллер команда, известная в НАСА как офицер по динамике полета, или в Европейское космическое агентство как штурман космического корабля.

Динамика полета зависит от двигательных дисциплин, аэродинамика, а астродинамика (орбитальная механика и небесная механика ). Его нельзя свести к простому контролю отношения; у реальных космических кораблей нет штурвалов или румпелей, как у самолетов или кораблей. В отличие от того, как изображаются вымышленные космические корабли, космический корабль на самом деле не кренится, чтобы развернуться в космическом пространстве, где его траектория полета строго зависит от действующих на него гравитационных сил и пропульсивные маневры применяемый.

Основные принципы

А космический аппарат полет определяется применением Ньютон с второй закон движения:

${\displaystyle \mathbf {F} =m\mathbf {a} ,}$

куда F это вектор сумма всех сил, действующих на транспортное средство, m - его текущая масса, и а - вектор ускорения, мгновенная скорость изменения скорости (v), которая, в свою очередь, представляет собой мгновенную скорость изменения смещения. Решение для а, ускорение равно сумме сил, деленной на массу. Ускорение интегрируется с течением времени для получения скорости, а скорость, в свою очередь, интегрируется для определения положения.

Расчеты динамики полета выполняются компьютеризированной системы наведения на борту транспортного средства; состояние динамики полета контролируется на земле во время механических маневров членом экипажа полетный контроллер команда, известная в НАСА с Центр космических полетов человека как офицер по динамике полета, или в Европейское космическое агентство как штурман космического корабля.^[1]

При полете в атмосфере с двигателем на летательный аппарат действуют три основные силы: движущая сила, аэродинамическая сила, и гравитация. Другие внешние силы, такие как центробежная сила, Сила Кориолиса, и давление солнечного излучения обычно незначительны из-за относительно короткого времени полета с двигателем и небольшого размера космического корабля, и ими можно пренебречь при упрощенных расчетах характеристик.^[2]

Движение

Тяга ракетный двигатель, в общем случае работы в атмосфере, аппроксимируется:^[3]

${\displaystyle F_{n}={\dot {m}}\;v_{e}={\dot {m}}\;v_{e-opt}+A_{e}(p_{e}-p_{amb})}$

куда:
${\displaystyle {\dot {m}}}$	= массовый расход выхлопных газов
${\displaystyle v_{e}}$	= эффективная скорость выхлопа (иногда обозначается иначе как c в публикациях)
${\displaystyle v_{e-opt}}$	= эффективная скорость струи, когда Pamb = Pe
${\displaystyle A_{e}}$	= проходное сечение в выходной плоскости сопла (или плоскости, в которой струя выходит из сопла при отрывном потоке)
${\displaystyle p_{e}}$	= статическое давление в выходной плоскости сопла
${\displaystyle p_{amb}}$	= окружающее (или атмосферное) давление

Эффективная скорость истечения ракетного топлива пропорциональна разряду вакуума. удельный импульс и подвержены влиянию атмосферного давления:^[4]

${\displaystyle {v_{e}}=(I_{sp-vac}-(A_{e}\,p_{amb})/{\dot {m}})\cdot g_{0}}$

куда:

${\displaystyle I_{sp-vac}}$ имеет единицы секунд

${\displaystyle g_{0}}$ это ускорение на поверхности Земли

Удельный импульс связывает дельта-v мощность к количеству израсходованного топлива в соответствии с Уравнение ракеты Циолковского:^[5]

${\displaystyle \Delta v\ =v_{e}\ln {\frac {m_{0}}{m_{1}}}}$

куда:

${\displaystyle m_{0}}$ начальная общая масса, включая топливо, в кг (или фунтах)

${\displaystyle m_{1}}$ окончательная общая масса в кг (или фунтах)

${\displaystyle v_{e}}$ эффективная скорость выхлопа в м / с (или фут / с)

${\displaystyle \Delta v\ }$ это дельта-v в м / с (или фут / с)

Атмосферная сила

Аэродинамические силы, присутствующие рядом с телом со значительной атмосферой, например земной шар, Марс или же Венера, анализируются как: поднимать, определяемая как составляющая силы, перпендикулярная направлению полета (не обязательно вверх для уравновешивания силы тяжести, как в случае самолета); и тащить, компонент, параллельный и противоположный направлению полета. Подъемная сила и сопротивление моделируются как произведение коэффициента, умноженного на динамическое давление действующие на эталонной площади:^[6]

${\displaystyle \mathbf {L} =C_{L}qA_{\text{ref}}}$

${\displaystyle \mathbf {D} =C_{D}qA_{\text{ref}}}$

куда:

• C_L примерно линейно с α, угол атаки между осью аппарата и направлением полета (до предельного значения), а при α = 0 для осесимметричного тела;
• C_D варьируется в зависимости от α²;
• C_L и C_D варьироваться в зависимости от Число Рейнольдса и число Маха;
• q, динамическое давление, равно 1/2 ρv², куда ρ плотность атмосферы, смоделированная для Земли как функция высоты в Международная стандартная атмосфера (используя предполагаемое распределение температуры, гидростатическое давление вариация, и закон идеального газа ); и
• А_ссылка - характерная площадь транспортного средства, такая как площадь поперечного сечения при максимальном диаметре.

Гравитация

Гравитационная сила, которую небесное тело оказывает на космический корабль, моделируется с телом и транспортным средством, взятыми как точечные массы; тела (Земля, Луна и т. д.) упрощены как сферы; а масса транспортного средства намного меньше массы тела, так что ее влиянием на гравитационное ускорение можно пренебречь. Следовательно, сила тяжести рассчитывается по формуле:

${\displaystyle \mathbf {W} =m\cdot g_{0}\left({\frac {r_{0}}{r}}\right)^{2}}$

куда:

${\displaystyle W}$ - сила тяжести (вес);

${\displaystyle m}$ - масса космического аппарата; и

${\displaystyle r}$ - радиальное расстояние транспортного средства до центра планеты; и

${\displaystyle r_{0}}$ - радиальное расстояние от поверхности планеты до ее центра; и

${\displaystyle g_{0}}$ это гравитационное ускорение на поверхности планеты

Орбитальный полет

Дальнейшая информация: Орбитальная механика

Орбитальная механика используется для расчета полета по орбите вокруг центрального тела. Для достаточно высоких орбит (обычно не менее 190 километров (100 морских миль) в случае Земли) аэродинамическая сила может считаться незначительной для относительно краткосрочных миссий (хотя может присутствовать небольшое сопротивление, которое приводит к распаду орбитальная энергия в течение более длительных периодов времени.) Когда масса центрального тела намного больше, чем у космического корабля, а другие тела находятся достаточно далеко, решение орбитальных траекторий можно рассматривать как задачу двух тел.^[7]

Можно показать, что в результате траектория в идеале является коническая секция (круг, эллипс, парабола или гипербола)^[8] с центральным телом, расположенным в одном фокусе. Орбитальные траектории представляют собой круги или эллипсы; параболическая траектория представляет собой первый выход транспортного средства из гравитационного поля центрального тела. Гиперболические траектории - это траектории ухода с избыточной скоростью, которые будут рассмотрены в разделе Межпланетный полет ниже.

Эллиптические орбиты характеризуются тремя элементами.^[7] Большая полуось а это среднее значение радиуса при апоапсис и периапсис:

${\displaystyle a={\frac {r_{a}+r_{p}}{2}}}$

В эксцентриситет е затем можно вычислить для эллипса, зная апсиды:

${\displaystyle e={\frac {r_{a}}{a}}-1}$

В период времени для полного обращения по орбите зависит только от большой полуоси и не зависит от эксцентриситета:^[9]

${\displaystyle TP=2\pi {\sqrt {\frac {a^{3}}{\mu }}}\,}$

куда ${\displaystyle \mu }$ это стандартный гравитационный параметр центрального тела.

Угловой орбитальные элементы космического корабля, вращающегося вокруг центрального тела, определяющего ориентацию орбиты относительно его основной плоскости отсчета

Ориентация орбиты в пространстве задается тремя углами:

• В склонность яплоскости орбиты с основной плоскостью (обычно это экваториальная плоскость планеты или Луны, или, в случае солнечной орбиты, плоскость орбиты Земли вокруг Солнца, известная как эклиптика.) Положительный наклон - на север, отрицательный - на юг.
• В долгота восходящего узла Ω, измеренный в фундаментальной плоскости против часовой стрелки, глядя на юге, от опорного направления (как правило, весеннее равноденствие ) до линии пересечения космическим аппаратом этой плоскости с юга на север. (Если наклон равен нулю, этот угол не определен и принимается равным 0.)
• В аргумент перицентра ω, измеряется в орбитальной плоскости против часовой стрелки, смотря на юг, от восходящего узла до перицентра. Если наклон равен 0, восходящего узла нет, поэтому ω измеряется от опорного направления. Для круговой орбиты нет перицентра, поэтому ω принимается равным 0.

Плоскость орбиты в идеале постоянна, но обычно подвержена небольшим возмущениям, вызванным планетарным сжатием и присутствием других тел.

Положение космического корабля на орбите определяется истинная аномалия, ${\displaystyle \nu }$, Угол измеряется от перицентра, или на круговую орбиту, от восходящего узла или опорного направления. В полу-латус прямой кишки, или радиус под углом 90 градусов от перицентра, составляет:^[10]

${\displaystyle p=a(1-e^{2})\,}$

Радиус в любом положении в полете составляет:

${\displaystyle r={\frac {p}{1+e\cos \nu }}\,}$

и скорость в этом положении:

${\displaystyle v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {1}{a}}\right)}}\,}$

Типы орбиты

Круговой

Для круговой орбиты р_а = р_п = а, а эксцентриситет равен 0. Круговая скорость на заданном радиусе равна:

${\displaystyle v_{c}={\sqrt {\frac {\mu }{r}}}\,}$

Эллиптический

Для эллиптической орбиты е больше 0, но меньше 1. Скорость перицентра:

${\displaystyle v_{p}={\sqrt {\frac {\mu (1+e)}{a(1-e)}}}\,}$

а скорость апоапсиса:

${\displaystyle v_{a}={\sqrt {\frac {\mu (1-e)}{a(1+e)}}}\,}$

Ограничивающим условием является параболическая орбита ухода, когда е = 1 и р_а становится бесконечным. Тогда скорость убегания в перицентре равна

${\displaystyle v_{e}={\sqrt {\frac {2\mu }{r_{p}}}}\,}$

Угол траектории полета

В удельный угловой момент любой конической орбиты, час, постоянна и равна произведению радиуса и скорости на перицентре. В любой другой точке орбиты он равен:^[11]

${\displaystyle h=rv\cos \varphi ,\,}$

куда φ угол траектории полета, отсчитываемый от местной горизонтали (перпендикулярно кр.) Это позволяет рассчитать φ в любой точке орбиты, зная радиус и скорость:

${\displaystyle \varphi =\arccos \left({\frac {r_{p}v_{p}}{rv}}\right)\,}$

Обратите внимание, что угол траектории полета является постоянным 0 градусов (90 градусов от местной вертикали) для круговой орбиты.

Истинная аномалия как функция времени

Можно показать, что приведенное выше уравнение углового момента также связывает скорость изменения истинной аномалии с р, v, и φ, таким образом, истинная аномалия может быть найдена как функция времени с момента прохождения перицентра путем интегрирования:^[12]

${\displaystyle \nu =r_{p}v_{p}\int _{t_{p}}^{t}{\frac {1}{r^{2}}}\,dt}$

И наоборот, время, необходимое для достижения данной аномалии, равно:

${\displaystyle t={\frac {1}{r_{p}v_{p}}}\int _{0}^{\nu }r^{2}\,d\nu }$

Орбитальные маневры

Смотрите также: Орбитальный маневр

Находясь на орбите, космический корабль может запускать ракетные двигатели, чтобы в самолете перейти на другую высоту или тип орбиты или изменить свою орбитальную плоскость. Эти маневры требуют изменения скорости корабля, а классическое ракетное уравнение используется для расчета потребности в топливе для заданного дельта-v. А дельта-v бюджет суммирует все потребности в порохе или определяет общую дельта-v, доступную для заданного количества пороха для миссии. Большинство маневров на орбите можно смоделировать как импульсивный, то есть как почти мгновенное изменение скорости с минимальной потерей точности.

Изменения в плоскости

Циркуляризация орбиты

Эллиптическую орбиту проще всего преобразовать в круговую орбиту в перицентре или апоапсисе, применив одно зажигание двигателя с дельтой v, равной разнице между желаемой круговой скоростью орбиты и скоростью перицентра или апоапсиса текущей орбиты:

Для округления перицентра делается ретроградный ожог:

${\displaystyle \Delta v\ =v_{c}-v_{p}\,}$

Для округления апоапсиса делают ожог посиградой:

${\displaystyle \Delta v\ =v_{c}-v_{a}\,}$

Изменение высоты трансфером Хоманна

Орбита перехода Хомана, 2, с орбиты (1) на более высокую орбиту (3)

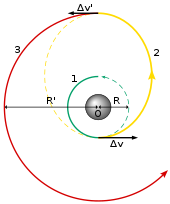
А Переходная орбита Хомана это простейший маневр, который можно использовать для перемещения космического корабля с одной высоты на другую. Требуются два ожога: первый для вывода аппарата на эллиптическую переходную орбиту, а второй - для циркуляции целевой орбиты.

Чтобы поднять круговую орбиту на ${\displaystyle v_{1}}$, первый ожог позиград увеличивает скорость до скорости перицентра переходной орбиты:

${\displaystyle \Delta v_{1}\ =v_{p}-v_{1}}$

Второй ожог позиград, сделанный в апоапсис, увеличивает скорость до скорости орбиты цели:

${\displaystyle \Delta v_{2}\ =v_{2}-v_{a}}$

Маневр опускания орбиты является зеркальным отображением маневра подъема; оба ожога сделаны ретроградными.

Изменение высоты биэллиптическим переносом

Биэллиптический переход с низкой круговой стартовой орбиты (темно-синий) на более высокую круговую орбиту (красный)

Чуть более сложный маневр изменения высоты - это двухэллиптический перенос, состоящий из двух полуэллиптических орбит; первый, позиградный ожог отправляет космический корабль на произвольно высокий апоапсис, выбранный в какой-то момент ${\displaystyle r_{b}}$ вдали от центрального тела. В этот момент второй ожог изменяет перицентр, чтобы он соответствовал радиусу конечной желаемой орбиты, где выполняется третий ретроградный ожог, чтобы вывести космический аппарат на желаемую орбиту.^[13] Хотя это занимает больше времени, для биэллиптического переноса может потребоваться меньшее количество топлива, чем для переноса Гомана, когда отношение начального радиуса орбиты к радиусу цели составляет 12 или больше.^[14][15]

Ожог 1 (посиград):

${\displaystyle \Delta v_{1}\ ={v_{p}}_{1}-v_{1}}$

Burn 2 (позиградный или ретроградный), чтобы согласовать перицентр с высотой целевой орбиты:

${\displaystyle \Delta v_{2}\ ={v_{a}}_{2}-{v_{a}}_{1}}$

Ожог 3 (ретроградный):

${\displaystyle \Delta v_{3}\ =v_{2}-{v_{p}}_{2}}$

Смена самолета

Маневры смены самолета могут выполняться отдельно или в сочетании с другими корректировками орбиты. Для маневра изменения плоскости чистого вращения, состоящего только из изменения наклона орбиты, удельного углового момента, час, начальной и конечной орбит равны по величине, но не по направлению. Следовательно, изменение удельного углового момента можно записать как:

${\displaystyle \Delta h=2h\sin \left({\frac {|\Delta i|}{2}}\right)}$

куда час - удельный угловой момент до смены плоскости, Δя - желаемое изменение угла наклона. Из этого можно показать^[16] что требуемая дельта-v является:

${\displaystyle \Delta v={\frac {2h\sin {\frac {|\Delta i|}{2}}}{r}}}$

Из определения час, это также можно записать как:

${\displaystyle \Delta v=2v\cos \varphi \sin \left({\frac {\left|\Delta i\right|}{2}}\right)}$

куда v - величина скорости до смены плоскости и φ - угол траектории полета. С использованием малоугловое приближение, это становится:

${\displaystyle \Delta v=v\cos(\varphi )\left|\Delta i\right|}$

Общая дельта-v для комбинированного маневра может быть рассчитан путем векторного сложения чистой дельты вращенияv и дельта-v для другого запланированного изменения орбиты.

Транслунный полет

Типичная транслунная траектория

Транспортные средства, отправляемые в лунные или планетные миссии, обычно не запускаются прямым впрыском на траекторию вылета, а сначала помещаются на низкую Землю парковочная орбита; это позволяет гибкость большего окно запуска и больше времени на проверку того, что машина находится в надлежащем состоянии для полета. Распространенное заблуждение состоит в том, что для полета на Луну требуется космическая скорость; это не так. Скорее, апогей транспортного средства поднят достаточно высоко, чтобы довести его до точки (прежде чем он достигнет апогея), где он войдет в гравитационное поле Луны. сфера влияния (хотя требуемая скорость близка к скорости убегания). Это определяется как расстояние от спутника, на котором его гравитационное притяжение на космический корабль равно силе его центрального тела, которое равно

${\displaystyle r_{\text{SOI}}=D\left({\frac {m_{s}}{m_{c}}}\right)^{2/5},}$

куда D - среднее расстояние от спутника до центрального тела, ам_c и м_s - массы центрального тела и спутника соответственно. Это значение составляет примерно 66 300 километров (35 800 морских миль) от Луны Земли.^[17]

Значительная часть полета транспортного средства (кроме непосредственной близости к Земле или Луне) требует точного решения как проблема трех тел, но предварительно можно смоделировать как исправленная коническая аппроксимация.

Транслунная инъекция

Основная статья: Транслунная инъекция

Это должно быть рассчитано таким образом, чтобы Луна была в положении, позволяющем захватить транспортное средство, и может быть смоделирована в первом приближении как передача Хомана. Однако продолжительность горения ракеты обычно достаточно велика и происходит при значительном изменении угла траектории полета, что не очень точно. Он должен быть смоделирован как неимпульсивный маневр, требуя интеграция к анализ методом конечных элементов ускорений, обусловленных движущей силой и силой тяжести, для получения скорости и угла траектории полета:^[18]

${\displaystyle {\dot {v}}={\frac {F\cos \alpha }{m}}-g\cos \theta \,}$

${\displaystyle {\dot {\theta }}={\frac {F\sin \alpha }{mv}}+\left({\frac {g}{v}}-{\frac {v}{r}}\right)\sin \theta ,\,}$

${\displaystyle v=\int _{t_{0}}^{t}{\dot {v}}\,dt}$

${\displaystyle \theta =\int _{t_{0}}^{t}{\dot {\theta }}\,dt}$

куда:

F - тяга двигателя;

α угол атаки;

м - масса автомобиля;

р - радиальное расстояние до центра планеты; и

грамм это гравитационное ускорение, которое зависит от обратного квадрата радиального расстояния:

${\displaystyle g=g_{0}\left({\frac {r_{0}}{r}}\right)^{2}\,}$^[18]

Высота ${\displaystyle h}$, расстояние вниз ${\displaystyle s}$, и радиальное расстояние ${\displaystyle r}$ от центра Земли затем вычисляются как:^[18]

${\displaystyle h=\int _{t_{0}}^{t}v\cos \theta \,dt}$

${\displaystyle r=r_{0}+h\,}$

${\displaystyle s=r_{0}\int _{t_{0}}^{t}{\frac {v}{r}}\sin \theta \,dt}$

Поправки в середине курса

Простая лунная траектория остается в одной плоскости, что приводит к пролету или орбите Луны в небольшом диапазоне наклона к экватору Луны. Это также допускает «свободный возврат», при котором космический корабль вернулся бы в подходящее положение для входа в атмосферу Земли, если бы он не был выведен на лунную орбиту. Для исправления ошибок траектории обычно требуются относительно небольшие изменения скорости. Такая траектория использовалась для Аполлон 8, Аполлон 10, Аполлон-11, и Аполлон-12 пилотируемые лунные миссии.

Большую гибкость в охвате лунной орбиты или места посадки (при больших углах наклона Луны) можно получить, выполняя маневр смены самолета в середине полета; однако это исключает возможность свободного возврата, поскольку новый самолет уведет траекторию аварийного возврата космического корабля от точки входа в атмосферу Земли и оставит космический корабль на высокой околоземной орбите. Этот тип траектории использовался в последних пяти миссиях Аполлона (с 13 по 17).

Вывод на лунную орбиту

в Программа Аполлон, выведение на ретроградную лунную орбиту было выполнено на высоте примерно 110 километров (59 морских миль) на обратной стороне Луны. Это стало перицинтионом начальных орбит с апоцинтионом порядка 300 километров (160 морских миль). Дельта v составляла приблизительно 1000 метров в секунду (3300 футов / с). Двумя орбитами позже орбита была сделана на 110 километров (59 морских миль). ^[19] Для каждой миссии специалист по динамике полета подготавливает 10 решений для вывода на лунную орбиту, чтобы можно было выбрать одно с оптимальным (минимальным) расходом топлива и наилучшим образом отвечающее требованиям миссии; это загружается в компьютер космического корабля и должно выполняться и контролироваться астронавтами на обратной стороне Луны, когда они находятся вне радиосвязи с Землей.^[19]

Межпланетный полет

Чтобы полностью покинуть гравитационное поле одной планеты, чтобы достичь другой, гиперболический необходима траектория относительно отлетающей планеты, при этом избыточная скорость добавляется (или вычитается из) орбитальной скорости отлетающей планеты вокруг Солнца. Желаемая гелиоцентрическая переходная орбита к высшая планета будет свое перигелий на отлетающей планете, что требует применения гиперболической избыточной скорости в направлении посиград, когда космический корабль находится далеко от Солнца. Для низшая планета пункт назначения, афелий будет на отправляемой планете, и избыточная скорость применяется в ретроградном направлении, когда космический корабль направлен к Солнцу. Для точных расчетов миссии элементы орбиты планет должны быть получены из эфемериды,^[20] Такие как это опубликовано Лабораторией реактивного движения НАСА.

Упрощение предположений

Тело	Эксцентриситет[21]	Иметь в виду расстояние 10^6 км[22]	Орбитальный скорость км / сек[22]	Орбитальный период годы[22]	Масса Земля = 1[22]	${\displaystyle \mu }$ км^3/ сек^2[22]
солнце	---	---	---	---	333,432	1,327x10^11
Меркурий	.2056	57.9	47.87	.241	.056	2,232x10^4
Венера	.0068	108.1	35.04	.615	.817	3,257 x 10^5
земной шар	.0167	149.5	29.79	1.000	1.000	3,986x10^5
Марс	.0934	227.8	24.14	1.881	.108	4,305x10^4
Юпитер	.0484	778	13.06	11.86	318.0	1,268x10^8
Сатурн	.0541	1426	9.65	29.46	95.2	3,795 x 10^7
Уран	.0472	2868	6.80	84.01	14.6	5,820x10^6
Нептун	.0086	4494	5.49	164.8	17.3	6,896 x 10^6

В целях предварительного анализа миссии и технико-экономического обоснования могут быть сделаны некоторые упрощенные допущения, позволяющие вычислить дельта-v с очень небольшой ошибкой:^[23]

• Орбиты всех планет, кроме Меркурий имеют очень малый эксцентриситет и поэтому могут считаться круговыми при постоянной орбитальной скорости и среднем расстоянии от Солнца.
• Орбиты всех планет (кроме Меркурия) почти компланарны с очень небольшим наклоном к эклиптика (3,39 градуса или меньше; наклон Меркурия 7,00 градусов).
• Возмущающие эффекты гравитации других планет незначительны.
• Космический корабль будет проводить большую часть своего полета только под гравитационным влиянием Солнца, за исключением коротких периодов, когда он находится в сфера влияния планет отправления и назначения.

Поскольку межпланетные космические аппараты проводят большой период времени в гелиоцентрическая орбита между планетами, которые находятся на относительно большом расстоянии друг от друга, приближение конической формы намного точнее для межпланетных траекторий, чем для транслунных траекторий.^[23] Точка пятна между гиперболической траекторией относительно исходной планеты и гелиоцентрической переходной орбитой находится в радиусе сферы влияния планеты относительно Солнца, как определено выше в Орбитальный полет. Учитывая соотношение масс Солнца в 333 432 раза больше массы Земли и расстояние 149 500 000 километров (80 700 000 морских миль), радиус сферы влияния Земли составляет 924 000 километров (499 000 морских миль) (примерно 1 000 000 километров).^[24]

Гелиоцентрическая переходная орбита

Переходная орбита, необходимая для переноса космического корабля с орбиты отправляемой планеты на планету назначения, выбирается из нескольких вариантов:

• А Переходная орбита Хомана требует как можно меньше метательного заряда и дельта-v; это половина эллиптической орбиты с афелий и перигелий по касательной к орбитам обеих планет, с наибольшим временем полета на выходе, равным половине периода эллипса. Это известно как соединение -классовая миссия.^[25][26] Варианта «свободного возврата» нет, потому что, если космический корабль не выйдет на орбиту вокруг планеты назначения, а вместо этого завершит переходную орбиту, планета вылета не будет в исходном положении. Использование еще одной передачи Хомана для возвращения требует значительного времени ожидания на планете назначения, что приводит к очень долгому общему времени полета туда и обратно.^[27] Писатель-фантаст Артур Кларк написал в своей книге 1951 года Исследование космоса что для полета туда и обратно с Земли на Марс потребуется 259 дней в обратном направлении и еще 259 дней в обратном направлении, с 425-дневным пребыванием на Марсе.
• Увеличение скорости апсиды отправления (и, следовательно, большой полуоси) приводит к траектории, которая пересекает орбиту планеты назначения не по касательной, прежде чем достигнет противоположной апсиды, увеличивая delta-v, но сокращая время прохождения на выходе ниже максимального.^[27]
• А помощь гравитации маневр, иногда известный как "маневр рогатки" или Крокко миссия после его автора 1956 г. Гаэтано Крокко, приводит к оппозиция -классовая миссия с гораздо более коротким временем пребывания в пункте назначения.^[28][26] Для этого нужно пролететь мимо другой планеты, используя ее гравитацию для изменения орбиты. Например, полет к Марсу и обратно можно значительно сократить с 943 дней, необходимых для миссии соединения, до менее чем года, если пролететь мимо Венеры по возвращении на Землю.

Гиперболический отъезд

Требуемая гиперболическая избыточная скорость v_∞ (иногда называют характеристическая скорость) - разница между скоростью вылета переходной орбиты и гелиоцентрической орбитальной скоростью уходящей планеты. Как только это будет определено, скорость впрыска относительно отлетающей планеты в перицентре будет:^[29]

${\displaystyle v_{p}={\sqrt {{\frac {2\mu }{r_{p}}}+v_{\infty }^{2}}}\,}$

Вектор избыточной скорости для гиперболы смещен от касательной к перицентру на характерный угол, поэтому инъекционный ожог перицентра должен опережать точку вылета планеты на тот же угол:^[30]

${\displaystyle \delta =\arcsin {\frac {1}{e}}\,}$

Геометрическое уравнение эксцентриситета эллипса нельзя использовать для гиперболы. Но эксцентриситет можно рассчитать из формулировок динамики как:^[31]

${\displaystyle e={\sqrt {1+{\frac {2\varepsilon h^{2}}{\mu ^{2}}}}},}$

где h - удельный угловой момент, как указано выше в Орбитальный полет сечение, рассчитанное по перицентру:^[30]

${\displaystyle h=r_{p}v_{p},\,}$

и ε это удельная энергия:^[30]

${\displaystyle \varepsilon ={\frac {v^{2}}{2}}-{\frac {\mu }{r}}\,}$

Кроме того, уравнения для r и v, приведенные в Орбитальный полет зависят от большой полуоси и поэтому не могут использоваться для траектории ухода. Но установка радиуса в перицентре равным уравнению r при нулевой аномалии дает альтернативное выражение для полу-латуса прямой кишки:

${\displaystyle p=r_{p}(1+e),\,}$

что дает более общее уравнение для зависимости радиуса от аномалии, которое можно использовать при любом эксцентриситете:

${\displaystyle r={\frac {r_{p}(1+e)}{1+e\cos \nu }}\,}$

Подстановка альтернативного выражения для p также дает альтернативное выражение для a (которое определено для гиперболы, но больше не представляет большую полуось). Это дает уравнение для зависимости скорости от радиуса, которое также можно использовать при любом эксцентриситете:

${\displaystyle v={\sqrt {\mu \left({\frac {2}{r}}-{\frac {(1-e^{2})}{r_{p}(1+e)}}\right)}}\,}$

Уравнения для угла траектории полета и аномалии в зависимости от времени приведены в Орбитальный полет также можно использовать для гиперболических траекторий.

Запустить окна

Из-за постоянно меняющегося относительного положения планет со временем изменение скорости, необходимое для миссии, сильно варьируется. Поэтому оптимальные окна запуска часто выбираются по результатам свиные участки которые показывают контуры характеристической энергии (v_∞²) в зависимости от времени отправления и прибытия.

Полет с приводом

Уравнения движения, используемые для описания полета транспортного средства во время запуска, могут составлять до шести степени свободы для расчетов в полете или с двумя степенями свободы для предварительной оценки характеристик. Расчет в полете займет факторы возмущения учитывать такие как земные сжатие и неравномерное распределение массы; и гравитационные силы всех близлежащих тел, включая Луну, Солнце и другие планеты. Предварительные оценки могут сделать некоторые упрощающие предположения: сферическая, однородная планета; транспортное средство можно представить как точечную массу; траектория полета предполагает двухкорпусную исправленная коническая аппроксимация; а местная траектория полета лежит в одной плоскости) с относительно небольшой потерей точности.^[18]

Векторы скорости, положения и силы, действующие на космический аппарат во время запуска

Общий случай запуска с Земли должен учитывать тягу двигателя, аэродинамические силы и гравитацию. Уравнение ускорения можно привести от векторного к скалярному виду, разрешив его тангенциальную форму (скорость ${\displaystyle v}$) и угловой (угол траектории полета ${\displaystyle \theta }$ относительно местной вертикали) компоненты скорости изменения времени относительно стартовой площадки. Таким образом, два уравнения становятся:

${\displaystyle {\dot {v}}={\frac {F\cos \alpha }{m}}-{\frac {D}{m}}-g\cos \theta \,}$

${\displaystyle {\dot {\theta }}={\frac {F\sin \alpha }{mv}}+{\frac {L}{mv}}+\left({\frac {g}{v}}-{\frac {v}{r}}\right)\sin \theta ,\,}$

куда:

F - тяга двигателя;

α угол атаки;

м - масса автомобиля;

D это автомобиль аэродинамическое сопротивление;

L это его аэродинамический подъемник;

р - радиальное расстояние до центра планеты; и

грамм это гравитационное ускорение, которое зависит от обратного квадрата радиального расстояния:

${\displaystyle g=g_{0}\left({\frac {r_{0}}{r}}\right)^{2}\,}$^[18]

Масса уменьшается по мере расходования топлива и ступени ракеты, двигатели или баки (если применимо).

Фиксированные на планете значения v и θ в любой момент полета определяются следующим образом: численное интегрирование двух скоростных уравнений с нуля (когда оба v и θ равны 0):

${\displaystyle v=\int _{t_{0}}^{t}{\dot {v}}\,dt}$

${\displaystyle \theta =\int _{t_{0}}^{t}{\dot {\theta }}\,dt}$

Анализ методом конечных элементов можно использовать для интегрирования уравнений, разбив полет на небольшие временные интервалы.

Для большинства ракеты-носители, генерируются относительно небольшие уровни подъемной силы, и гравитационный поворот используется, в основном, в зависимости от третьего члена уравнения угловой скорости. В момент отрыва, когда угол и скорость равны нулю, уравнение тета-точки имеет вид математически неопределенный и не может быть оценен до тех пор, пока скорость не станет отличной от нуля вскоре после старта. Но обратите внимание, что в этом состоянии единственная сила, которая может заставить транспортное средство крениться, - это тяга двигателя, действующая при ненулевом угле атаки (первый член) и, возможно, небольшой подъемной силе (второй член), до тех пор, пока достигается нулевой угол тангажа. В гравитационном повороте тангаж инициируется увеличением угла атаки (с помощью тяга двигателя на кардане ) с последующим постепенным уменьшением угла атаки на протяжении оставшейся части полета.^[18][32]

Если известны скорость и угол траектории полета, высота ${\displaystyle h}$ и расстояние вниз ${\displaystyle s}$ вычисляются как:^[18]

Векторы скорости и силы, действующие на космический аппарат при механическом спуске и посадке

${\displaystyle h=\int _{t_{0}}^{t}v\cos \theta \,dt}$

${\displaystyle r=r_{0}+h\,}$

${\displaystyle s=r_{0}\int _{t_{0}}^{t}{\frac {v}{r}}\sin \theta \,dt}$

Фиксированные на планете значения v и θ преобразуются в фиксированные по пространству (инерционные) значения со следующими преобразованиями:^[18]

${\displaystyle v_{s}={\sqrt {v^{2}+2\omega rv\cos \varphi \sin \theta \sin A_{z}+(\omega r\cos \theta )^{2}}},}$

куда ω скорость вращения планеты в радианах в секунду, φ - широта стартовой позиции, а А_z это запуск азимут угол.

${\displaystyle \theta _{s}=\arccos \left({\frac {v\cos \theta }{v_{s}}}\right)}$

Финал v_s, θ_s и р должен соответствовать требованиям целевой орбиты, как определено орбитальной механикой (см. Орбитальный полет, выше), где final v_s обычно является требуемой перицентрической (или круговой) скоростью, а конечная θ_s составляет 90 градусов. Анализ механического спуска будет использовать ту же процедуру с обратными граничными условиями.

Вход в атмосферу

Основная статья: Вход в атмосферу

Контролируемый вход, спуск и посадка транспортного средства достигается за счет сброса избыточной кинетической энергии через аэродинамический обогрев от перетаскивания, что требует некоторых средств теплозащита, и / или ретроградная тяга. Конечный спуск обычно достигается с помощью парашюты и / или воздушные тормоза.

Контроль отношения

Основная статья: Контроль отношения

Поскольку космические корабли большую часть своего полета проводят без двигателя по инерции, вакуум В космосе они отличаются от самолетов тем, что их траектория полета не определяется их положением (ориентацией), за исключением полета в атмосфере для управления силами подъемной силы и сопротивления и во время полета с двигателем для выравнивания вектора тяги. Тем не менее, управление ориентацией часто поддерживается в полете без двигателя, чтобы удерживать космический корабль в фиксированной ориентации для целей астрономическое наблюдение, коммуникации, или для солнечная энергия поколение; или поместить его в контролируемое вращение для пассивного терморегулирование, или для создания искусственной гравитации внутри корабля.

Контроль отношения поддерживается по отношению к инерциальной системе отсчета или другому объекту (небесной сфере, определенным полям, близлежащим объектам и т. Д.). Положение корабля описывается углами по отношению к трем взаимно перпендикулярным осям вращения, называемым креном, тангажем и рысканием. Ориентация может быть определена путем калибровки с использованием внешней системы наведения, такие, как определение углов к опорной звезды или Солнца, то внутренне контролируется с помощью инерциальной системы механического или оптического гироскопы. Ориентация - это векторная величина, описываемая тремя углами для мгновенного направления и мгновенными скоростями крена по всем трем осям вращения. Аспект управления подразумевает как осведомленность о мгновенной ориентации и скорости крена, так и возможность изменять скорость крена, чтобы принять новую ориентацию, используя либо система управления реакцией или другими способами.

Второй закон Ньютона, применяемый к вращательному, а не линейному движению, принимает следующий вид:^[33]

${\displaystyle \mathbf {\tau _{x}} =I_{x}\mathbf {\alpha _{x}} ,}$

куда ${\displaystyle \mathbf {\tau _{x}} }$ это сеть крутящий момент вокруг оси вращения транспортного средства, I_Икс это его момент инерции вокруг этой оси (физическое свойство, объединяющее массу и ее распределение вокруг оси), и ${\displaystyle {alpha_{x}}}$ это угловое ускорение вокруг этой оси в радианах в секунду в секунду. Следовательно, скорость ускорения в градусах в секунду в секунду равна

${\displaystyle \mathbf {\alpha _{x}} =(180/\pi )\mathbf {\tau _{x}} /I_{x},}$

Угловая скорость вращения аналогична линейному движению. ${\displaystyle \mathbf {\omega _{x}} }$ (градусов в секунду) получается путем интегрирования α через некоторое время:

${\displaystyle {\omega _{x}}=\int _{t_{0}}^{t}{\alpha _{x}}dt}$

и угловой поворот ${\displaystyle \mathbf {\theta _{x}} }$ - временной интеграл от ставки:

${\displaystyle \theta _{x}=\int _{t_{0}}^{t}{\omega _{x}}dt}$

Три основных момента инерции I_Икс, Я_у, и я_z по осям крена, тангажа и рыскания определяются через центр массы.

Управляющий крутящий момент для ракеты-носителя иногда аэродинамически обеспечивается подвижными ребрами, и обычно установка двигателей на карданы направить тягу вокруг центра масс. Крутящий момент часто применяется к космическим кораблям, работающим в отсутствие аэродинамических сил, посредством система управления реакцией, набор подруливающих устройств, расположенных вокруг транспортного средства. Двигатели запускаются либо вручную, либо под автоматическим управлением, короткими очередями для достижения желаемой скорости вращения, а затем запускаются в противоположном направлении, чтобы остановить вращение в желаемом положении. Крутящий момент вокруг конкретной оси составляет:

${\displaystyle \mathbf {\tau } =\sum _{i=1}^{N}(r_{i}\times \mathbf {F_{i}} ),}$

куда р это расстояние от центра масс, а F - тяга отдельного двигателя малой тяги (только составляющая F перпендикулярно р Включено.)

В ситуациях, когда потребление топлива может быть проблемой (например, для длительных спутников или космических станций), могут использоваться альтернативные средства для обеспечения управляющего крутящего момента, такие как колеса реакции^[34] или же гироскопы контрольного момента.^[35]

Примечания

1. "ESA - Flight Dynamics". Европейское космическое агентство. Получено 22 июня, 2020.
2. Бейт, Мюллер и Уайт (1971), стр. 11-12.
3. Джордж П. Саттон и Оскар Библарц (2001). Элементы силовой установки ракеты (7-е изд.). Wiley Interscience. ISBN  0-471-32642-9. См. Уравнение 2-14.
4. Саттон, Джордж П .; Библарц, Оскар (2001). Элементы силовой установки ракеты. Джон Вили и сыновья. ISBN  978-0-471-32642-7. В архиве из оригинала 12 января 2014 г.. Получено 28 мая 2016.
5. Джордж П. Саттон и Оскар Библарц (2001). Элементы силовой установки ракеты (7-е изд.). Wiley Interscience. ISBN  0-471-32642-9. См. Уравнение 3-33.
6. Андерсон (2004) С. 257–261.
7. Перри (1967), п. 11: 151.
8. Бейт, Мюллер и Уайт (1971) С. 11-40.
9. Бейт, Мюллер и Уайт (1971), п. 33.
10. Бейт, Мюллер и Уайт (1971), п. 24.
11. Бейт, Мюллер и Уайт (1971), п. 18.
12. Бейт, Мюллер и Уайт (1971) С. 31-32.
13. Кертис, Ховард (2005). Орбитальная механика для студентов инженерных специальностей. Эльзевир. п. 264. ISBN  0-7506-6169-0.
14. Gobetz, F.W .; Долл, Дж. Р. (май 1969 г.). «Обзор импульсных траекторий». Журнал AIAA. Американский институт аэронавтики и астронавтики. 7 (5): 801–834. Bibcode:1969AIAAJ ... 7..801D. Дои:10.2514/3.5231.
15. Эскобаль, Педро Р. (1968). Методы астродинамики. Нью-Йорк: Джон Уайли и сыновья. ISBN  978-0-471-24528-5.
16. Hintz (2015), п. 112.
17. Бейт, Мюллер и Уайт (1971) С. 333–334.
18. Кромис (1967), п. 11: 154.
19. О'Брайен, Фрэнк (1999). "Выход на лунную орбиту". Журнал полета Аполлона. Дэвид Вудс. Получено 25 июня, 2020.
20. Бейт, Мюллер и Уайт (1971), п. 359.
21. «Кеплеровские элементы для 1800–2050 гг.» Лаборатория реактивного движения солнечной системы. Получено 17 декабря 2009.
22. Бейт, Мюллер и Уайт (1971), п. 361.
23. Бейт, Мюллер и Уайт (1971) С. 359, 362.
24. Бейт, Мюллер и Уайт (1971), п. 368.
25. Mattfeld et al. (2015), п. 3.
26. Дрейк и др. 2017 г..
27. Бейт, Мюллер и Уайт (1971) С. 362–363.
28. Mattfeld et al. (2015), стр. 3–4.
29. Бейт, Мюллер и Уайт (1971), п. 369.
30. Бейт, Мюллер и Уайт (1971), п. 371.
31. Бейт, Мюллер и Уайт (1971), п. 372.
32. Гласстон (1965), п. 209, §4.97.
33. Пиво и Джонстон (1972), п. 499.
34. "Колесо реакции / импульса". НАСА. Получено 15 июн 2018.
35. "Извлеченные уроки гироскопа момента управления космической станцией" (PDF). NASA.gov.

Рекомендации

• Андерсон, Джон Д. (2004), Введение в полет (5-е изд.), Макгроу-Хилл, ISBN  0-07-282569-3
• Бейт, Роджер Б .; Мюллер, Дональд Д .; Уайт, Джерри Э. (1971), Основы астродинамики, Дувр
• Пиво, Фердинанд П .; Джонстон, Рассел младший (1972), Векторная механика для инженеров: статика и динамика, Макгроу-Хилл
• Дрейк, Брет Дж .; Бейкер, Джон Д .; Хоффман, Стефан Дж .; Ландау, Дэймон; Воелс, Стивен А. (2017). «Варианты траектории для исследования Марса и спутников Марса». Команда НАСА по архитектуре пилотируемых космических полетов (презентация).
• Фелленц, Д. (1967). «Атмосферный вход». В Теодоре Баумейстере (ред.). Стандартный справочник Марка для инженеров-механиков (Седьмое изд.). Нью-Йорк: Макгроу Хилл. С. 11: 155–58. ISBN  0-07-142867-4.
• Гласстон, Сэмюэл (1965). Справочник по космическим наукам. D. Van Nostrand Company, Inc.
• Хинц, Джеральд Р. (2015). Орбитальная механика и астродинамика: методы и инструменты для космических полетов. Чам. ISBN  9783319094441. OCLC  900730410.
• Кромис, А.Дж. (1967). "Анализ траектории полета с приводом". В Теодоре Баумейстере (ред.). Стандартный справочник Марка для инженеров-механиков (Седьмое изд.). Нью-Йорк: Макгроу Хилл. С. 11: 154–55. ISBN  0-07-142867-4.
• Мэттфельд, Брайан; Стромгрен, Чел; Шайфейс, Хилари; Комар, Дэвид Р .; Чирилло, Уильям; Гудлифф, Кандис (2015). «Обмен между классами оппозиции и конъюнктуры для первых миссий человека на Марс» (PDF). Получено 10 июля, 2018.
• Перри, W.R. (1967). «Орбитальная механика». В Теодоре Баумейстере (ред.). Стандартный справочник Марка для инженеров-механиков (Седьмое изд.). Нью-Йорк: Макгроу Хилл. С. 11: 151–52. ISBN  0-07-142867-4.
• Рассел, Дж. (1967). «Механика лунного и межпланетного полета». В Теодоре Баумейстере (ред.). Стандартный справочник Марка для инженеров-механиков (Седьмое изд.). Нью-Йорк: Макгроу Хилл. С. 11: 152–54. ISBN  0-07-142867-4.
• Сиди, М.Дж. "Динамика и управление космическими аппаратами. Кембридж, 1997".
• Томсон, В.Т. «Введение в космическую динамику». Дувр, 1961.
• Верц, Дж. Р. "Определение положения космического аппарата и управление им". Kluwer, 1978.
• Визель, W.E. «Динамика космического полета». Макгроу-Хилл, 1997.