Окончание фильтра изображения - Image filter end terminations
| Линейный аналог электронные фильтры |
|---|
|
Простые фильтры |
- Обзор фильтров изображений см. фильтр составного изображения.
Фильтры разработан с использованием импеданс изображения Методология страдает специфическим недостатком теории. Прогнозируемые характеристики фильтра вычисляются в предположении, что фильтр заканчивается собственным импедансом изображения на каждом конце. Обычно это не так; фильтр будет иметь фиксированные сопротивления. Это приводит к отклонению отклика фильтра от теоретического. В этой статье объясняется, как эффекты конец фильтра изображения можно принять во внимание.
Как правило, оконечные нагрузки вызывают округление частотной характеристики при отсечении. Метод изображения предсказывает резкий скачок в наклоне отклика при отсечении, что не реализуется на практике, хотя хорошо спроектированный фильтр изображения может приблизиться к этому. Другой прогноз метода изображения - нулевая потеря полоса пропускания (при условии идеальных компонентов без потерь). Опять же, это не может быть достигнуто на практике, потому что отражения от концевых выводов всегда вызывают некоторые потери.
- Части этой статьи или раздела основаны на знании читателем сложного сопротивление представление конденсаторы и индукторы и на знании частотная область представление сигналов.
Символы, использованные в этой статье
Импеданс
- то импеданс изображения в конце 1
- сопротивление изображения в конце 2
- сопротивление изображения, когда оба конца идентичны
- оконечное сопротивление на конце 1
- оконечное сопротивление на конце 2
- оконечное сопротивление, когда оба конца идентичны
Коэффициенты
- то коэффициент отражения в конце 1
- коэффициент отражения на конце 2
- коэффициент отражения, когда оба конца идентичны
- то коэффициент передачи в конце 1
- коэффициент передачи на конце 2
- комплекс коэффициент распространения фильтра
- то коэффициент затухания фильтра
- то фазовый коэффициент фильтра
Обратите внимание, что все эти коэффициенты определяются относительно импеданса изображения, а не фактического входного импеданса фильтра.
Общий случай

Передаточная функция любого фильтра, подключенного, как показано на диаграмме выше, определяется выражением
куда
Обратите внимание, что Vя это номинальное напряжение, которое было бы выдано генератором, если бы он был ограничен его характеристическим сопротивлением (т. е. р1), а не фактическое напряжение, появляющееся на входных клеммах фильтра.
Далее можно отметить, что первая часть выражения,
- ,
такой же, как выражение для передаточной функции без учета торцевых окончаний. Таким образом, вторая часть выражения - это часть отклика, вызванная несогласованными импедансами;
Симметричный корпус
Где фильтр симметричный сопротивление изображения и окончания, выражение может быть значительно уменьшено. Обратите внимание, что не требуется, чтобы фильтр был симметричным внутри, только чтобы концевые секции имели одинаковый импеданс изображения, обращенный к одинаковым оконечным сопротивлениям.
Дальнейшее упрощение можно сделать, если в фильтре нет резистивных потерь (или предполагается, что ими можно пренебречь). В этом случае импеданс изображения чисто реальный (ря) в полосе пропускания и чисто мнимой (iXя) в полосе задерживания. Величина передаточной функции определяется выражением
где для полосы пропускания,
а для полосы задерживания
Антиметрический корпус
Аналогичное упрощение можно сделать для без потерь антиметрический фильтры. В этом случае замена
превращается в общее уравнение. Для полосы пропускания
а для полосы задерживания
Антиметрический, в этом контексте, означает, что сопротивление изображения фильтра и окончания на каждом конце являются двойной друг друга. Это будет иметь место, если фильтр имеет последовательную и шунтирующую секции того же типа, соответственно, на каждом конце. Симметричные фильтры имеют четное количество полусекций, а антиметрические фильтры - нечетное количество полусекций. В подавляющем большинстве случаев конструкция фильтра будет симметричной или антиметрической, и будет применяться одно из этих сокращенных выражений.
Некоторые примеры графиков ответов
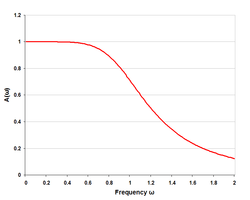 Отклик низкочастотного прототип Т-фильтр с учетом влияния резистивных оконечных заделок | |
 Отклик того же Т-фильтра с удаленным теоретическим откликом. То есть составляющая отклика обусловлена только эффектами оконечных окончаний. |
Смотрите также
- Импеданс изображения
- Фильтр составного изображения
- Двойной импеданс
- Фильтр прототипа
- Категория: Фильтры импеданса изображения
Рекомендации
- Маттеи, Янг, Джонс Микроволновые фильтры, сети согласования импеданса и структуры связи, стр 68-72, McGraw-Hill 1964.















![{displaystyle A (iomega) = {frac {V_ {o}} {V_ {i}}} = {sqrt {frac {Z_ {I2}} {Z_ {I1}}}} e ^ {- gamma} left [{ frac {au _ {I1} au _ {I2}} {1-e ^ {- 2gamma} r_ {I1} r_ {I2}}} ight]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76e9302e29805bb2b4de91543363bec086456af8)





![{displaystyle left [{frac {au _ {I1} au _ {I2}} {1-e ^ {- 2gamma} r_ {I1} r_ {I2}}} ight].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5eb12bcf02ede759fe0c646265e8453160f35cb1)
![{displaystyle A (iomega) = e ^ {- gamma} left [{frac {4Z_ {I} R} {(R + Z_ {I}) ^ {2} -e ^ {- 2gamma} (R-Z_ {I) }) ^ {2}}} ight]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/226a60fe1eb49709c78075721166bfb46495868c)






