RC схема - RC circuit

А цепь резистор-конденсатор (RC схема), или же RC фильтр или же RC сеть, является электрическая цепь состоит из резисторы и конденсаторы. Это может быть вызвано Напряжение или же Источник тока и они будут давать разные ответы. RC-цепь первого порядка состоит из одного резистора и одного конденсатора и представляет собой простейший тип RC-цепи.

RC-цепи могут использоваться для фильтрации сигнала путем блокировки определенных частот и пропуска других. Двумя наиболее распространенными RC-фильтрами являются фильтры верхних частот и фильтры нижних частот; полосовые фильтры и полосовые фильтры обычно требуется RLC фильтры, хотя грубые можно сделать с помощью RC-фильтров.

Вступление

Есть три основных линейных пассивных сосредоточенный аналоговая схема компоненты: резистор (R), конденсатор (C) и индуктор (L). Их можно объединить в RC-цепочку, Цепь RL, то LC-цепь, а Схема RLC, с акронимами, указывающими, какие компоненты используются. Эти схемы, в том числе, демонстрируют большое количество важных типов поведения, которые являются фундаментальными для большей части аналоговая электроника. В частности, они могут действовать как пассивные фильтры. В этой статье рассматривается RC-схема как в серии и параллельно формы, как показано на схемах ниже.

Естественный ответ

RC схема

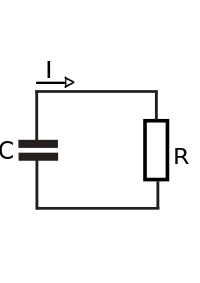
Простейшая RC-схема состоит из резистора и заряженного конденсатора, соединенных друг с другом в один контур, без внешнего источника напряжения. Как только цепь замыкается, конденсатор начинает разряжать накопленную энергию через резистор. Напряжение на конденсаторе, зависящее от времени, можно найти, используя Действующий закон Кирхгофа. Ток через резистор должен быть равным по величине (но противоположным по знаку) производной по времени накопленного заряда на конденсаторе. Это приводит к линейное дифференциальное уравнение

${\displaystyle C{\frac {dV}{dt}}+{\frac {V}{R}}=0\,,}$

куда C - емкость конденсатора.

Решение этого уравнения для V дает формулу для экспоненциальный спад:

${\displaystyle V(t)=V_{0}e^{-{\frac {t}{RC}}}\,,}$

куда V₀ напряжение конденсатора в момент времени т = 0.

Время, необходимое для падения напряжения до V₀/е называется Постоянная времени RC и дается,^[1]

${\displaystyle \tau =RC\,.}$

В этой формуле τ измеряется в секундах, р в омах и C в фарадах.

Комплексный импеданс

В комплексное сопротивление, Z_C (в Ом ) конденсатора емкостью C (в фарады ) является

${\displaystyle Z_{C}={\frac {1}{sC}}}$

В комплексная частота s в целом комплексное число,

${\displaystyle s=\sigma +j\omega \,,}$

куда

• j представляет мнимая единица: j² = −1,
• σ это экспоненциальный спад постоянный (в неперс в секунду), и
• ω это синусоидальный угловая частота (в радиан в секунду ).

Синусоидальное установившееся состояние

Синусоидальное установившееся состояние - это особый случай, когда входное напряжение состоит из чистой синусоиды (без экспоненциального затухания). Как результат, ${\displaystyle \sigma =0}$ и сопротивление становится

${\displaystyle Z_{C}=-{\frac {j}{\omega C}}\,.}$

Последовательная схема

Серии RC схема

Рассматривая схему как делитель напряжения, то Напряжение на конденсаторе:

${\displaystyle V_{C}(s)={\frac {\frac {1}{Cs}}{R+{\frac {1}{Cs}}}}V_{\mathrm {in} }(s)={\frac {1}{1+RCs}}V_{\mathrm {in} }(s)}$

а напряжение на резисторе равно:

${\displaystyle V_{R}(s)={\frac {R}{R+{\frac {1}{Cs}}}}V_{\mathrm {in} }(s)={\frac {RCs}{1+RCs}}V_{\mathrm {in} }(s)\,.}$

Передаточные функции

В функция передачи от входного напряжения до напряжения на конденсаторе

${\displaystyle H_{C}(s)={\frac {V_{C}(s)}{V_{\mathrm {in} }(s)}}={\frac {1}{1+RCs}}\,.}$

Точно так же передаточная функция от входа к напряжению на резисторе равна

${\displaystyle H_{R}(s)={\frac {V_{R}(s)}{V_{\rm {in}}(s)}}={\frac {RCs}{1+RCs}}\,.}$

Полюсы и нули

Обе передаточные функции имеют единую столб расположен в

${\displaystyle s=-{\frac {1}{RC}}\,.}$

Кроме того, передаточная функция для напряжения на резисторе имеет нуль расположен в источник.

Усиление и фаза

Величина выигрыша по двум компонентам равна

${\displaystyle G_{C}={\big |}H_{C}(j\omega ){\big |}=\left|{\frac {V_{C}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}}$

и

${\displaystyle G_{R}={\big |}H_{R}(j\omega ){\big |}=\left|{\frac {V_{R}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}\,,}$

а фазовые углы равны

${\displaystyle \phi _{C}=\angle H_{C}(j\omega )=\tan ^{-1}\left(-\omega RC\right)}$

и

${\displaystyle \phi _{R}=\angle H_{R}(j\omega )=\tan ^{-1}\left({\frac {1}{\omega RC}}\right)\,.}$

Эти выражения вместе могут быть заменены на обычное выражение для фазор представляющий вывод:

${\displaystyle {\begin{aligned}V_{C}&=G_{C}V_{\mathrm {in} }e^{j\phi _{C}}\\V_{R}&=G_{R}V_{\mathrm {in} }e^{j\phi _{R}}\,.\end{aligned}}}$

Текущий

Ток в цепи везде одинаковый, так как цепь включена последовательно:

${\displaystyle I(s)={\frac {V_{\mathrm {in} }(s)}{R+{\frac {1}{Cs}}}}={\frac {Cs}{1+RCs}}V_{\mathrm {in} }(s)\,.}$

Импульсивный ответ

В импульсивный ответ для каждого напряжения обратное Преобразование Лапласа соответствующей передаточной функции. Он представляет собой реакцию схемы на входное напряжение, состоящее из импульса или Дельта-функция Дирака.

Импульсная характеристика напряжения конденсатора равна

${\displaystyle h_{C}(t)={\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)={\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,}$

куда ты(т) это Ступенчатая функция Хевисайда и τ = RC это постоянная времени.

Точно так же импульсная характеристика для напряжения резистора равна

${\displaystyle h_{R}(t)=\delta (t)-{\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)=\delta (t)-{\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,}$

куда δ(т) это Дельта-функция Дирака

Соображения в частотной области

Это частотная область выражения. Их анализ покажет, какие частоты схемы (или фильтры) пропускают, а какие отклоняют. Этот анализ основан на рассмотрении того, что происходит с этими коэффициентами усиления, когда частота становится очень большой и очень маленькой.

В качестве ω → ∞:

${\displaystyle G_{C}\to 0\quad {\mbox{and}}\quad G_{R}\to 1\,.}$

В качестве ω → 0:

${\displaystyle G_{C}\to 1\quad {\mbox{and}}\quad G_{R}\to 0\,.}$

Это показывает, что если выходной сигнал подается через конденсатор, высокие частоты ослабляются (замыкаются на землю), а низкие частоты проходят. Таким образом, схема ведет себя как фильтр нижних частот. Однако, если выходной сигнал поступает через резистор, высокие частоты пропускаются, а низкие частоты ослабляются (поскольку конденсатор блокирует сигнал, когда его частота приближается к 0). В этой конфигурации схема ведет себя как фильтр высоких частот.

Диапазон частот, который пропускает фильтр, называется его пропускная способность. Точка, в которой фильтр ослабляет сигнал до половины его нефильтрованной мощности, называется его частота среза. Это требует, чтобы коэффициент усиления схемы был уменьшен до

${\displaystyle G_{C}=G_{R}={\frac {1}{\sqrt {2}}}}$.

Решение вышеуказанного уравнения дает

${\displaystyle \omega _{\mathrm {c} }={\frac {1}{RC}}\quad {\mbox{or}}\quad f_{\mathrm {c} }={\frac {1}{2\pi RC}}}$

это частота, которую фильтр будет ослаблять до половины своей исходной мощности.

Ясно, что фазы также зависят от частоты, хотя в целом этот эффект менее интересен, чем изменения усиления.

В качестве ω → 0:

${\displaystyle \phi _{C}\to 0\quad {\mbox{and}}\quad \phi _{R}\to 90^{\circ }={\frac {\pi }{2}}{\mbox{ radians}}\,.}$

В качестве ω → ∞:

${\displaystyle \phi _{C}\to -90^{\circ }=-{\frac {\pi }{2}}{\mbox{ radians}}\quad {\mbox{and}}\quad \phi _{R}\to 0\,.}$

Так что на ОКРУГ КОЛУМБИЯ (0 Гц ), напряжение конденсатора находится в фазе с напряжением сигнала, а напряжение резистора опережает его на 90 °. По мере увеличения частоты напряжение на конденсаторе запаздывает на 90 ° относительно сигнала, а напряжение на резисторе оказывается синфазным с сигналом.

Соображения во временной области

Этот раздел основан на знании е, то натуральная логарифмическая константа.

Самый простой способ получить поведение во временной области - использовать Преобразования Лапласа выражений для V_C и V_р приведено выше. Это эффективно преобразует jω → s. Предполагая пошаговый ввод (т.е. V_в = 0 перед т = 0 а потом V_в = V после):

${\displaystyle {\begin{aligned}V_{\mathrm {in} }(s)&=V\cdot {\frac {1}{s}}\\V_{C}(s)&=V\cdot {\frac {1}{1+sRC}}\cdot {\frac {1}{s}}\\V_{R}(s)&=V\cdot {\frac {sRC}{1+sRC}}\cdot {\frac {1}{s}}\,.\end{aligned}}}$

Переходная характеристика напряжения конденсатора.

Отклик на скачок напряжения резистора.

Неполные фракции разложения и обратное Преобразование Лапласа урожай:

${\displaystyle {\begin{aligned}V_{C}(t)&=V\left(1-e^{-{\frac {t}{RC}}}\right)\\V_{R}(t)&=Ve^{-{\frac {t}{RC}}}\,.\end{aligned}}}$

Эти уравнения предназначены для расчета напряжения на конденсаторе и резисторе соответственно, когда конденсатор зарядка; для разряда уравнения обратные. Эти уравнения можно переписать в терминах заряда и тока, используя соотношения C = Q/V и V = ИК (видеть Закон Ома ).

Таким образом, напряжение на конденсаторе стремится к V со временем напряжение на резисторе стремится к 0, как показано на рисунках. Это соответствует интуитивному выводу, что конденсатор со временем будет заряжаться от напряжения питания и в конечном итоге будет полностью заряжен.

Эти уравнения показывают, что последовательная RC-цепь имеет постоянная времени, обычно обозначается τ = RC время, за которое напряжение на компоненте либо повышается (на конденсаторе), либо падает (на резисторе) с точностью до 1/е от его окончательного значения. То есть, τ время, которое требуется V_C достигать V(1 − 1/е) и V_р достигать V(1/е).

Скорость изменения дробный 1 − 1/е на τ. Таким образом, при переходе от т = Nτ к т = (N + 1)τ, напряжение сместится примерно на 63,2% от своего уровня на т = Nτ к его окончательному значению. Таким образом, конденсатор будет заряжен примерно до 63,2% после τ, и практически полностью заряжен (99,3%) примерно через 5τ. Когда источник напряжения заменяется коротким замыканием, когда конденсатор полностью заряжен, напряжение на конденсаторе падает экспоненциально с т из V до 0. Конденсатор разрядится примерно до 36,8% после τ, и практически полностью разряжается (0,7%) примерно через 5τ. Обратите внимание, что текущий, я, в цепи ведет себя так же, как напряжение на резисторе, через Закон Ома.

Эти результаты также могут быть получены путем решения дифференциальные уравнения описание схемы:

${\displaystyle {\begin{aligned}{\frac {V_{\mathrm {in} }-V_{C}}{R}}&=C{\frac {dV_{C}}{dt}}\\V_{R}&=V_{\mathrm {in} }-V_{C}\,.\end{aligned}}}$

Первое уравнение решается с помощью интегрирующий фактор а второй легко следует; решения точно такие же, как полученные с помощью преобразований Лапласа.

Интегратор

Рассмотрим выход на конденсаторе при высоко частота, т.е.

${\displaystyle \omega \gg {\frac {1}{RC}}\,.}$

Это означает, что у конденсатора недостаточно времени для зарядки, поэтому его напряжение очень мало. Таким образом, входное напряжение приблизительно равно напряжению на резисторе. Чтобы убедиться в этом, рассмотрим выражение для ${\displaystyle I}$ приведено выше:

${\displaystyle I={\frac {V_{\mathrm {in} }}{R+{\frac {1}{j\omega C}}}}\,,}$

но обратите внимание, что описанное частотное условие означает, что

${\displaystyle \omega C\gg {\frac {1}{R}}\,,}$

так

${\displaystyle I\approx {\frac {V_{\mathrm {in} }}{R}}}$

что просто Закон Ома.

Сейчас же,

${\displaystyle V_{C}={\frac {1}{C}}\int _{0}^{t}I\,dt\,,}$

так

${\displaystyle V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{\mathrm {in} }\,dt\,,}$

который является интегратор через конденсатор.

Дифференциатор

Рассмотрим выход на резисторе при низкий частота т. е.

${\displaystyle \omega \ll {\frac {1}{RC}}\,.}$

Это означает, что конденсатор успевает зарядиться, пока его напряжение почти не сравняется с напряжением источника. Учитывая выражение для я снова, когда

${\displaystyle R\ll {\frac {1}{\omega C}}\,,}$

так

${\displaystyle {\begin{aligned}I&\approx {\frac {V_{\mathrm {in} }}{\frac {1}{j\omega C}}}\\V_{\mathrm {in} }&\approx {\frac {I}{j\omega C}}=V_{C}\,.\end{aligned}}}$

Сейчас же,

${\displaystyle {\begin{aligned}V_{R}&=IR=C{\frac {dV_{C}}{dt}}R\\V_{R}&\approx RC{\frac {dV_{in}}{dt}}\,,\end{aligned}}}$

который является дифференциатор через резистор.

Более точным интеграция и дифференциация может быть достигнуто путем размещения резисторов и конденсаторов на входе и Обратная связь петля операционные усилители (видеть интегратор операционного усилителя и дифференциатор операционного усилителя ).

Параллельная схема

Параллельный RC схема

Параллельная RC-цепь обычно менее интересна, чем последовательная. Во многом это связано с тем, что выходное напряжение V_из равно входному напряжению V_в - в результате эта схема не действует как фильтр входного сигнала, если только не подается Источник тока.

Со сложными сопротивлениями:

${\displaystyle {\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=j\omega CV_{\mathrm {in} }\,.\end{aligned}}}$

Это показывает, что ток конденсатора на 90 ° сдвинут по фазе с током резистора (и источника). В качестве альтернативы можно использовать определяющие дифференциальные уравнения:

${\displaystyle {\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=C{\frac {dV_{\mathrm {in} }}{dt}}\,.\end{aligned}}}$

При питании от источника тока передаточная функция параллельной RC-цепи равна:

${\displaystyle {\frac {V_{\mathrm {out} }}{I_{\mathrm {in} }}}={\frac {R}{1+sRC}}\,.}$

Синтез

Иногда требуется синтезировать RC-цепь из заданного рациональная функция в s. Чтобы синтез пассивных элементов был возможен, функция должна быть положительно-действительная функция. Чтобы синтезировать как RC-схему, все критические частоты (полюса и нули ) должен располагаться на отрицательной действительной оси и чередоваться между полюсами и нулями с равным количеством каждого. Кроме того, критическая частота, ближайшая к началу координат, должна быть полюсом, если предположить, что рациональная функция представляет собой импеданс, а не полную проводимость.

Синтез может быть осуществлен с помощью модификации Способствовать синтезу или же Синтез Кауэра используется для синтеза LC-схемы. В случае синтеза Кауэра a лестничная сеть резисторов и конденсаторов.^[2]

Смотрите также

• Цепь RL
• LC-цепь
• Схема RLC
• Электрическая сеть
• Список тем электроники
• Шаговый ответ

Рекомендации

1. Горовиц и Хилл, стр. 1.13
2. Бакши и Бакши, стр. 3-30–3-37.

Библиография

• Bakshi, U.A .; Бакши, А.В., Анализ схем - II, Технические публикации, 2009 г. ISBN  9788184315974.
• Горовиц, Пол; Хилл, Уинфилд, Искусство электроники (3-е издание), Cambridge University Press, 2015 г. ISBN  0521809266.