Периодическая бегущая волна - Periodic travelling wave

О всплеске волн, наблюдаемом в квантовой механике, см. Волновой пакет.
Схематическое изображение периодической бегущей волны
Периодическая бегущая волна

В математике периодическая бегущая волна (или же волновой поезд) это периодическая функция одного-размерный Космос который движется с постоянной скоростью. Следовательно, это особый тип пространственно-временного колебание это периодическая функция как пространства, так и времени.

Периодические бегущие волны играют фундаментальную роль во многих математических уравнениях, включая автоколебательные системы,[1][2] возбудимые системы[3] исистемы реакция – диффузия – адвекция.[4] Уравнения этих типов широко используются как математические модели биологии, химии и физики, и многие примеры явлений, напоминающих периодические бегущие волны, были обнаружены эмпирически.

Математическая теория периодических бегущих волн наиболее полно разработана для уравнения в частных производных, но эти решения также встречаются в ряде других типов математических систем, включая интегродифференциальные уравнения,[5][6] интегро-разностные уравнения,[7]решетки связанных карт[8]и клеточные автоматы[9][10]

Периодические бегущие волны не только важны сами по себе, но и как одномерный эквивалент спиральные волны и целевые шаблоны в двумерном пространстве и волны прокрутки в трехмерном пространстве.

История исследования

Периодические бегущие волны были впервые изучены в 1970-х годах. Ключевой ранней исследовательской работой была статья Нэнси Копелл и Лу Ховард[1] доказав несколько фундаментальных результатов о периодических бегущих волнах в уравнения реакции-диффузии. За этим последовала значительная исследовательская деятельность в 1970-х и начале 1980-х годов. Был период бездействия, прежде чем интерес к периодическим бегущим волнам был возобновлен математической работой по их генерации.[11][12] и по их обнаружению в экология в наборах пространственно-временных данных о циклических популяциях.[13][14] С середины 2000-х годов в исследованиях периодических бегущих волн использовались новые вычислительные методы для изучения их стабильность и абсолютная стабильность.[15][16]

Семьи

Существование периодических бегущих волн обычно зависит от параметр значения в математическом уравнении. Если существует решение с периодической бегущей волной, то обычно существует семейство таких решений с разными скоростями волн. Для уравнений в частных производных периодические бегущие волны обычно возникают в непрерывном диапазоне волновых скоростей.[1]

Стабильность

Важный вопрос: является ли периодическая бегущая волна стабильный или же неустойчивый как решение исходной математической системы. Для уравнений с частными производными типично, что семейство волн подразделяется на стабильный и неустойчивый части.[1][17][18] Для нестабильных периодических бегущих волн важный дополнительный вопрос заключается в том, являются ли они абсолютно или конвективно неустойчивыми, что означает наличие или отсутствие стационарных растущих линейных режимов.[19] Эта проблема была решена только для нескольких дифференциальных уравнений в частных производных.[2][15][16]

Поколение

В настоящее время хорошо изучен ряд механизмов генерации периодических бегущих волн. К ним относятся:

  • Неоднородность: пространственный шум в значениях параметров может генерировать серию полос периодических бегущих волн.[20] Это важно в приложениях для колебательные химические реакции, где примеси могут вызывать узоры мишеней или спиральные волны, которые являются двумерными обобщениями периодических бегущих волн. Этот процесс послужил мотивацией для большей части работ по периодическим бегущим волнам в 1970-х и начале 1980-х годов. Неоднородность ландшафта также была предложена как причина периодических бегущих волн, наблюдаемых в экологии.[21]
  • Вторжения, которые могут оставлять за собой периодическую бегущую волну.[11][12][22] Это важно в Тейлор – Куэтт система при наличии протока,[23] в химических системах, таких как Реакция Белоусова – Жаботинского[24][25] И в хищная добыча системы в экология.[26][27]
  • Волны, порожденные граничным условием Дирихле
    Волны, порожденные граничным условием Дирихле на центральном отверстии
    Границы домена с Дирихле или же Робин граничные условия.[28][29][30] Это потенциально важно в экология, где условия Робина или Дирихле соответствуют границе между средой обитания и окружающей враждебной средой. Однако окончательный эмпирическое доказательство по причине волн трудно получить для экологических систем.
  • Миграция вызвана преследование и уклонение.[31] Это может иметь значение в экология.
  • Миграция между субпопуляциями,[32] который снова имеет потенциал экологический значимость.

Во всех этих случаях ключевым вопросом является выбор члена семейства периодических бегущих волн. Для большинства математических систем это остается открытой проблемой.

Пространственно-временной хаос

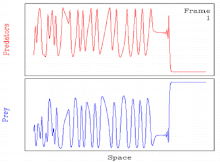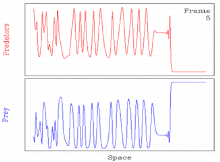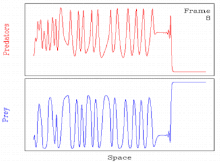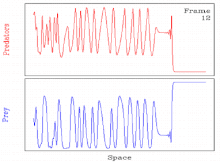
Периодические бегущие волны и хаос при моделировании нашествия хищников на добычу

Обычно некоторые параметр значений периодические бегущие волны, возникающие в результате механизма генерации волн, неустойчивы. В таких случаях решение обычно становится пространственно-временным. хаос.[11][27] Таким образом, решение включает пространственно-временной переход к хаосу через периодическую бегущую волну.

Лямбда – омега-системы и комплексное уравнение Гинзбурга – Ландау.

Существуют две определенные математические системы, которые служат прототипами периодических бегущих волн и имеют фундаментальное значение для развития математического понимания и теории. Это "лямбда-омега" класс уравнения реакции-диффузии[1]

(р=(ты2+v2)1/2) и комплекс Гинзбург – Ландау уравнение.[2]

(А комплекснозначный). Отметим, что эти системы одинаковы, если λ (р)=1-р2, ω (р)=-c р2 и б= 0. Обе системы можно упростить, переписав уравнения в терминах амплитуды (р или |А|) и фаза (arctan (v/ты) или arg А). После того, как уравнения были переписаны таким образом, легко увидеть, что решения с постоянной амплитудой являются периодическими бегущими волнами, а фаза является линейной функцией от Космос и время. Следовательно, ты и v, или Re (А) и я(А), находятся синусоидальный функции пространства и времени.

Эти точные решения для семейств периодических бегущих волн позволяют провести большой объем дальнейших аналитических исследований. Точные условия для стабильность периодических бегущих волн можно найти,[1][2] а условие абсолютной устойчивости сводится к решению простого многочлен.[15][16] Получены также точные решения задачи отбора волн, порождаемых вторжениями.[22][33] и нулевыми граничными условиями Дирихле.[34][35] В последнем случае для комплексного уравнения Гинзбурга – Ландау полным решением является стационарная дыра Нодзаки-Бекки.[34][36]

Большая часть работ по периодическим бегущим волнам в комплексном уравнении Гинзбурга – Ландау содержится в физика литературе, где они обычно известны как плоские волны.

Численный расчет периодических бегущих волн и их устойчивости

Для большинства математических уравнений аналитический Расчет периодических решений бегущей волны невозможен, поэтому необходимо выполнить численные расчеты. За уравнения в частных производных, обозначим через Икс и т (одномерный) Космос и временные переменные соответственно. Тогда периодические бегущие волны являются функциями переменной бегущей волны z=Икс-c т. Подставляя эту форму решения в уравнения в частных производных дает систему обыкновенные дифференциальные уравнения известны как уравнения бегущей волны. Периодическим бегущим волнам соответствуют предельные циклы этих уравнений, и это дает основу для численные расчеты. Стандартный вычислительный подход: числовое продолжение уравнений бегущей волны. Сначала выполняется продолжение устойчивое состояние найти Бифуркация хопфа точка. Это отправная точка для ветви (семейства) периодических решений с бегущей волной, за которой можно проследить числовое продолжение. В некоторых (необычных) случаях оба конца ветви (семейства) периодических решений с бегущей волной имеют вид гомоклиника решения,[37] в этом случае необходимо использовать внешнюю отправную точку, такую ​​как численное решение уравнения в частных производных.

Периодическая бегущая волна стабильность можно также рассчитать численно, вычислив спектр. Это облегчается тем фактом, что спектр решений периодических бегущих волн уравнений в частных производных полностью состоит из существенный спектр.[38] Возможные численные подходы включают метод Хилла.[39] и численное продолжение спектра.[15] Одним из преимуществ последнего подхода является то, что его можно расширить для вычисления границ в параметр пространство между устойчивыми и неустойчивыми волнами[40]

Программного обеспечения: Свобода, программное обеспечение с открытым исходным кодом пакет Wavetrain http://www.ma.hw.ac.uk/wavetrain предназначен для численного исследования периодических бегущих волн.[41] С помощью числовое продолжение, Wavetrain может рассчитывать форму и устойчивость решений периодических бегущих волн для уравнений в частных производных, а также области пространства параметров, в которых волны существуют и в которых они устойчивы.

Приложения

Найденные примеры явлений, напоминающих периодические бегущие волны эмпирически включая следующее.

  • Многие природные популяции претерпевают многолетние циклы обилия. В некоторых случаях эти популяционные циклы пространственно организованы в периодическую бегущую волну. Такое поведение было обнаружено в полевки в Фенноскандии[13] и север Великобритании,[14] геометрические бабочки в Северной Фенноскандии,[42] почки лиственницы в европейских Альпах[21] и тетерев в Шотландии.[43]
  • В полупустыни, растительность часто самоорганизуется в пространственные узоры.[44] На склонах это обычно состоит из полос растительности, идущих параллельно контуры, разделенные полосами голой земли; этот тип полосатой растительности иногда называют Куст тигра. Многие наблюдательные исследования сообщают о медленном движении полос в направлении вверх.[45] Однако в ряде других случаев данные явно указывают на стационарные модели,[46] и вопрос о движении остается спорным. Вывод, который наиболее согласуется с имеющимися данными, состоит в том, что некоторые полосы растительности перемещаются, а другие - нет.[47] Паттерны первой категории имеют форму периодических бегущих волн.
  • Бегущие полосы встречаются в колебательный и возбудимый химические реакции. Они наблюдались в 1970-х гг. В Реакция Белоусова – Жаботинского[48] и они послужили важной мотивацией для математической работы, проделанной в то время над периодическими бегущими волнами. В более поздних исследованиях также использовалась возможность связать экспериментально наблюдаемые полосы с математической теорией периодических бегущих волн посредством подробного моделирования.[49]
  • Периодические бегущие волны возникают на Солнце, как часть солнечный цикл.[50][51] Они являются следствием зарождения солнечного магнитное поле посредством солнечное динамо. Таким образом, они связаны с солнечные пятна.
  • В гидродинамика, конвекция шаблоны часто включают периодические бегущие волны. Конкретные примеры включают конвекцию бинарной жидкости[52] и конвекция нагретой проволоки.[53]
  • Образцы периодической формы бегущей волны возникают в «нестабильности принтера», когда тонкий зазор между двумя вращающимися ацентрическими цилиндрами заполнен маслом.[54]

Смотрите также

Рекомендации

  1. ^ а б c d е ж Н. Копелл, Л. Ховард (1973) "Плоские волновые решения уравнений реакции-диффузии", Stud. Appl. Математика. 52: 291–328.
  2. ^ а б c d И. С. Арансон, Л. Крамер (2002) "Мир комплексного уравнения Гинзбурга – Ландау", Ред. Мод. Phys. 74: 99–143. DOI: 10.1103 / RevModPhys.74.99
  3. ^ С. Кумбс (2001) "От периодических бегущих волн к бегущим фронтам в модели дендритных волн" спайк-диффузный спайк ", Математика. Biosci. 170: 155–172.DOI: 10.1016 / S0025-5564 (00) 00070-5
  4. ^ J.A. Шерратт, Дж. Дж. Лорд (2007) "Нелинейная динамика и бифуркации рисунка в модели полос растительности в полузасушливых средах", Теор. Popul. Биол. 71 (2007): 1–11.DOI: 10.1016 / j.tpb.2006.07.009
  5. ^ С. А. Горли, Н. Ф. Бриттон (1993) "Неустойчивость решений бегущей волны популяционной модели с нелокальными эффектами", IMA J. Appl. Математика. 51: 299–310.DOI: 10.1093 / imamat / 51.3.299
  6. ^ П. Эшвин, М. В. Бартучелли, Т. Дж. Бриджес, С. А. Горли (2002) "Бегущие фронты для уравнения КПП с пространственно-временной задержкой", З. Энгью. Математика. Phys. 53: 103–122.DOI: 0010-2571 / 02 / 010103-20
  7. ^ М. Кот (1992) "Бегущие волны в дискретном времени: экологические примеры", J. Math. Биол. 30: 413-436. DOI: 10.1007 / BF00173295
  8. ^ М. Д. С. Эррера, Дж. С. Мартин (2009) "Аналитическое исследование решеток связанных отображений синхронизированных состояний и бегущих волн, а также их каскадов удвоения периода", Хаос, солитоны и фракталы 42: 901–910.DOI: 10.1016 / j.chaos.2009.02.040
  9. ^ Дж. А. Шеррат (1996) "Периодические бегущие волны в семействе детерминированных клеточных автоматов", Physica D 95: 319–335.DOI: 10.1016 / 0167-2789 (96) 00070-X
  10. ^ М. Курбидж (1997) "Об изобилии бегущих волн в одномерных бесконечных клеточных автоматах", Physica D 103: 133–144.DOI: 10.1016 / S0167-2789 (96) 00256-4
  11. ^ а б c Дж. А. Шеррат (1994) "Нерегулярные бодрствования в реакционно-диффузионных волнах", Physica D 70: 370–382. DOI: 10.1016 / 0167-2789 (94) 90072-8
  12. ^ а б С.В. Петровский, Х. Мальхов (1999) "Минимальная модель формирования паттернов в системе жертва-хищник", Математика. Комп. Моделирование 29: 49–63. DOI: 10.1016 / S0895-7177 (99) 00070-9
  13. ^ а б Э. Ранта, В. Кайтала (1997) "Бегущие волны в динамике популяции полевок", Природа 390: 456. DOI: 10.1038 / 37261
  14. ^ а б X. Lambin, D. A. Elston, S. J. Petty, J. L. MacKinnon (1998) "Пространственная асинхронность и периодические бегущие волны в циклических популяциях полевок", Proc. R. Soc. Лондон. В 265: 1491–1496. DOI: 10.1098 / rspb.1998.0462
  15. ^ а б c d J.D.M. Радемахер, Б. Сандстеде, А. Шил (2007) «Вычисление абсолютных и существенных спектров с использованием продолжения», Physica D 229: 166–183. DOI: 10.1016 / j.physd.2007.03.016
  16. ^ а б c М. Дж. Смит, Дж. Д. М. Радемахер, Дж. А. Шеррат (2009) "Абсолютная стабильность волновых цепей может объяснить пространственно-временную динамику в реакционно-диффузионных системах типа лямбда-омега", SIAM J. Appl. Дин. Системы 8: 1136–1159. DOI: 10.1137 / 090747865
  17. ^ К. Магину (1981) "Устойчивость периодических решений бегущей волны с большими пространственными периодами в реакционно-диффузионных системах", J. Diff. Уравнения. 39: 73–99.10.1016 / 0022-0396 (81) 90084-X
  18. ^ M. J. Smith, J.A. Шерратт (2007) "Влияние неравных коэффициентов диффузии на периодические бегущие волны в колебательных реакционно-диффузионных системах", Physica D 236: 90–103. DOI: 10.1016 / j.physd.2007.07.013
  19. ^ Б. Сандстеде, А. Шеель (2000) "Абсолютная и конвективная неустойчивость волн в неограниченных и больших ограниченных областях", Physica D 145: 233–277.DOI: 10.1016 / S0167-2789 (00) 00114-7
  20. ^ А. Л. Кей, Дж. А. Шеррат (2000) "Пространственный шум стабилизирует периодические волновые структуры в колебательных системах на конечных областях", SIAM J. Appl. Математика. 61: 1013–1041.DOI: 10.1137 / S0036139999360696
  21. ^ а б Д. М. Джонсон, О. Н. Бьорнстад, A.M. Либхольд (2006) «Пейзажная мозаика вызывает бегущие волны нашествий насекомых», Oecologia 148: 51–60.DOI: 10.1007 / s00442-005-0349-0
  22. ^ а б К. Нозаки, Н. Бекки (1983) "Выбор паттернов и пространственно-временной переход к хаосу в уравнении Гинзбурга – Ландау", Phys. Rev. Lett. 51: 2171-2174. DOI: 10.1103 / PhysRevLett.51.2171
  23. ^ А. Цамерет, В. Стейнберг (1994) "Конкурирующие состояния в системе Куэтта – Тейлора с осевым потоком", Phys. Ред. E 49: 4077-4086. DOI: 10.1103 / PhysRevE.49.4077
  24. ^ М. Ипсен, Л. Крамер, П.Г. Соренсен (2000) "Амплитудные уравнения для описания химических реакционно-диффузионных систем", Phys. Rep. 337: 193–235.DOI: 10.1016 / S0370-1573 (00) 00062-4
  25. ^ В КАЧЕСТВЕ. Михайлов, К. Шоуолтер (2006) "Контроль волн, структур и турбулентности в химических системах", Phys. Rep. 425: 79–194. DOI: 10.1016 / j.physrep.2005.11.003
  26. ^ J.A. Шерратт, М. А. Льюис, А. К. Фаулер (1995) "Экологический хаос после вторжения", Proc. Natl. Акад. Sci. Соединенные Штаты Америки 92: 2524–2528.10.1073 / пнас.92.7.2524
  27. ^ а б С.В. Петровский, Х. Мальхов (2001) "Волна хаоса: новый механизм формирования паттернов в пространственно-временной динамике населения", Теор. Поп. Биол. 59: 157–174.DOI: 10.1006 / tpbi.2000.1509
  28. ^ Дж. А. Шеррат, X. Ламбин, К. Дж. Томас, Т. Н. Шеррат (2002) "Генерация периодических волн особенностями ландшафта в системах циклический хищник-жертва" Proc. R. Soc. Лондон. В 269: 327–334.DOI: 10.1098 / rspb.2001.1890
  29. ^ М. Зибер, Х. Мальхов, С.В. Петровский (2010) "Шумовое подавление периодических бегущих волн в колебательных реакционно-диффузионных системах", Proc. R. Soc. Лондон. A 466: 1903–1917.DOI: 10.1098 / rspa.2009.0611
  30. ^ J.A. Sherratt (2008) "Сравнение периодической генерации бегущей волны граничными условиями Робина и Дирихле в колебательных уравнениях реакции-диффузии". IMA J. Appl. Математика. 73: 759-781.DOI: 10.1093 / imamat / hxn015
  31. ^ Бикташев В.Н., Цыганов М.А. (2009) «Спонтанные бегущие волны в колебательных системах с перекрестной диффузией», Phys. Ред. E 80: искусство. нет. 056111.DOI: 10.1103 / PhysRevE.80.056111
  32. ^ М. Р. Гарви, М. Голински (2010) "Динамика метапопуляции для пространственно протяженных взаимодействий хищник – жертва", Экологическая сложность 7: 55–59.DOI: 10.1016 / j.ecocom.2009.05.001
  33. ^ Дж. А. Шеррат (1994) "Об эволюции периодических плоских волн в уравнениях реакции-диффузии типа λ-ω", SIAM J. Appl. Математика. 54: 1374–1385. DOI: 10.1137 / S0036139993243746
  34. ^ а б Н. Бекки, К. Нозаки (1985) "Формирование пространственных структур и отверстий в обобщенном уравнении Гинзбурга – Ландау", Phys. Lett. А 110: 133–135.DOI: 10.1016 / 0375-9601 (85) 90759-5
  35. ^ Дж. А. Шеррат (2003) "Периодическая селекция бегущей волны граничными условиями Дирихле в колебательных реакционно-диффузионных системах", SIAM J. Appl. Математика. 63: 1520–1538. DOI: 10.1137 / S0036139902392483
  36. ^ J. Lega (2001) "Решения с подвижной дырой комплексного уравнения Гинзбурга – Ландау: обзор", Physica D 152: 269–287. DOI: 10.1016 / S0167-2789 (01) 00174-9
  37. ^ E. J. Doedel, J. P. Kernevez (1986) "AUTO: программное обеспечение для задач продолжения и бифуркации в обыкновенных дифференциальных уравнениях", Отчет по прикладной математике, Калифорнийский технологический институт, Пасадена, США
  38. ^ Раздел 3.4.2 Б. Сандстеде (2002) "Устойчивость бегущих волн". В: Б. Фидлер (ред.) Справочник динамических систем II, Северная Голландия, Амстердам, стр. 983–1055. http://www.dam.brown.edu/people/sandsted/publications/survey-stability-of-waves.pdf В архиве 2013-09-27 в Wayback Machine
  39. ^ Б. Деконинк, Дж. Н. Куц (2006) "Вычисление спектров линейных операторов методом Флоке – Фурье – Хилла", J. Comput. Phys. 219: 296–321. DOI: 10.1016 / j.jcp.2006.03.020
  40. ^ J. A. Sherratt (2013) "Численное продолжение границ в пространстве параметров между устойчивыми и неустойчивыми решениями периодической бегущей волны (волнового потока) уравнений в частных производных", Adv. Comput. Математика, в прессе. DOI: 10.1007 / s10444-012-9273-0
  41. ^ J.A. Sherratt (2012) "Методы численного продолжения для изучения решений периодических бегущих волн (волновых цепей) уравнений в частных производных",Appl. Математика. Вычисление 218: 4684–4694. DOI: 10.1016 / j.amc.2011.11.005
  42. ^ А. К. Нильссен, О. Тенов, Х. Байлунд (2007) "Волны и синхронность в Epirrita autumnata / Operophtera brumata вспышки II. Активность солнечных пятен не может объяснить циклические вспышки ", J. Animal Ecol. 76: 269–275.DOI: 10.1111 / j.1365-2656.2006.01205.x / full
  43. ^ Р. Мосс, Д.А. Элстон, А. Уотсон (2000) "Пространственная асинхронность и демографические бегущие волны во время популяционных циклов тетерева", Экология 81: 981-989. DOI: 10.1890 / 0012-9658
  44. ^ M. Rietkerk, S.C. Dekker, P.C. де Руйтер, Дж. ван де Коппель (2004) «Самоорганизованная неоднородность и катастрофические сдвиги в экосистемах», Наука 305: 1926–1929.DOI: 10.1126 / science.1101867
  45. ^ К. Валентин, Ж. М. д'Эрб, Дж. Пузен (1999) "Почвенные и водные компоненты полосчатой ​​растительности", Катена 37: 1-24. DOI: 10.1016 / S0341-8162 (99) 00053-3
  46. ^ Д. Л. Дункерли, К. Дж. Браун (2002) "Косая полосатость растительности в засушливой зоне Австралии: значение для теорий эволюции и сохранения структуры", J. Arid Environ. 52: 163–181. DOI: 10.1006 / jare.2001.0940
  47. ^ В. Деблаув (2010) "Модуляция структур автоорганизмов растительности в среде / Самоорганизованная модуляция структуры растительности в засушливом климате". Кандидатская диссертация, Свободный университет Брюсселя.«Архивная копия». Архивировано из оригинал в 2013-09-27. Получено 2013-01-09.CS1 maint: заархивированная копия как заголовок (связь)
  48. ^ Н. Копелл, Л. Ховард (1973) "Горизонтальные полосы в реакции Белоусова", Наука 180: 1171–1173. DOI: 10.1126 / science.180.4091.1171
  49. ^ Г. Бордюгов, Н. Фишер, Х. Энгель, Н. Манц, О. Стейнбок (2010) "Аномальная дисперсия в реакции Белоусова – Жаботинского: эксперименты и моделирование", Physica D 239: 766–775. DOI: 10.1016 / j.physd.2009.10.022
  50. ^ М.Р.Е. Проктор (2006) "Действие динамо и солнце". В: M. Rieutord, B. Dubrulle (ред.) Динамика звездной жидкости и численное моделирование: от Солнца до нейтронных звезд, EAS Publications Series 21: 241–273. http://www.damtp.cam.ac.uk/user/mrep/solcyc/paper.pdf
  51. ^ Проктор М. Р., Шпигель Э. А. (1991) "Волны солнечной активности". В: Солнце и холодные звезды: активность, магнетизм, динамо (конспект лекций по физике 380) С. 117–128.DOI: 10.1007 / 3-540-53955-7_116
  52. ^ Э. Каплан, В. Стейнберг (1993) "Проскальзывание фазы, неадиабатический эффект и динамика источника бегущих волн", Phys. Rev. Lett. 71: 3291–3294. DOI: 10.1103 / PhysRevLett.71.3291
  53. ^ Л. Пастур, М. Т. Вестра, Д. Сноук, В. ван де Уотер, М. ван Хекке, К. Сторм, В. ван Саарлоос (2003) "Источники и дыры в одномерном эксперименте по конвекции бегущей волны", Phys. Ред. E 67: арт. нет. 036305. DOI: 10.1103 / PhysRevE.67.036305
  54. ^ П. Хабдас, М. Дж. Кейс, Дж. Р. де Брюйн (2001) «Поведение дефектов стока и истока в одномерном образце движущихся пальцев», Phys. Ред. E 63: арт. № 066305.DOI: 10.1103 / PhysRevE.63.066305