Тетрагемигексаэдр - Tetrahemihexahedron - Wikipedia
| Тетрагемигексаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 7, E = 12 V = 6 (χ = 1) |
| Лица по сторонам | 4{3}+3{4} |
| Символ Wythoff | 3/2 3 | 2 (двойное покрытие) |
| Группа симметрии | Тd, [3,3], *332 |
| Указатель ссылок | U04, C36, W67 |
| Двойной многогранник | Тетрагемигексакрон |
| Фигура вершины |  3.4.3/2.4 |
| Акроним Bowers | Thah |

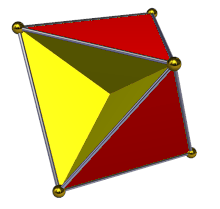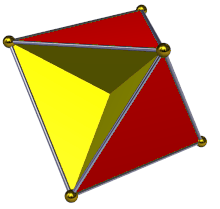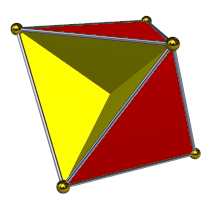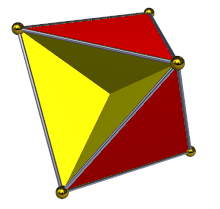
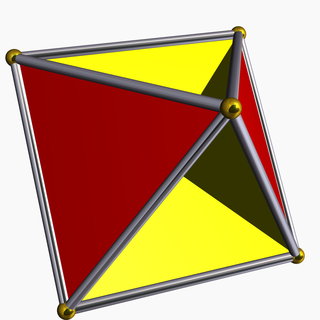
В геометрия, то тетрагемигексаэдр или же гемикубооктаэдр это однородный звездный многогранник, индексируется как U4. Имеет 7 граней (4 треугольники и 3 квадраты ), 12 ребер и 6 вершин.[1] Его вершина фигуры это скрещенный четырехугольник. Его Диаграмма Кокстера – Дынкина является ![]()
![]()
![]()
![]()
![]()
![]()
![]() (хотя это двойное покрытие тетрагемигексаэдра).
(хотя это двойное покрытие тетрагемигексаэдра).
Это единственный не-призматический однородный многогранник с нечетным количеством граней. Его Символ Wythoff является 3/2 3 | 2, но это представляет собой двойное покрытие тетрагемигексаэдра восемью треугольниками и шестью квадратами, спаренными и совпадающими в пространстве. (Более интуитивно это можно рассматривать как два совпадающих тетрагемигексаэдра.)
Это гемиполиэдр. Часть имени «полу» означает, что некоторые грани образуют группу с половиной меньшего числа членов, чем какой-нибудь правильный многогранник - здесь три квадратные грани образуют группу с половиной граней правильного шестигранника, более известного как куб - следовательно полугексаэдр. Грани полукруга также ориентированы в том же направлении, что и грани правильного многогранника. Три квадратные грани тетрагемигексаэдра, как и три лицевых стороны куба, взаимно перпендикуляр.
Характеристика «половинного числа» также означает, что полуграки должны проходить через центр многогранника, где все они пересекаются друг с другом. Визуально каждый квадрат делится на четыре прямоугольные треугольники, с двумя видимыми с каждой стороны.
Связанные поверхности
Это неориентируемый поверхность. Он уникален как единственный равномерный многогранник с Эйлерова характеристика 1 и, следовательно, является проективный многогранник, давая представление о реальная проективная плоскость[2] очень похоже на Римская поверхность.
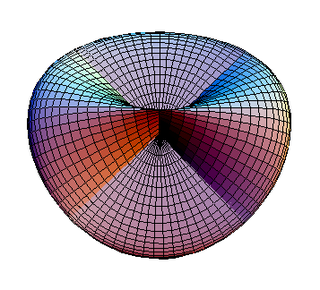 Римская поверхность |
Связанные многогранники
Он имеет те же вершины и ребра, что и обычный октаэдр. Он также разделяет 4 из 8 треугольных граней октаэдра, но имеет три дополнительных квадратных грани, проходящих через центр многогранника.
 Октаэдр |  Тетрагемигексаэдр |
Двойная фигура - это тетрагемигексакрон.
это 2-крытый посредством кубооктаэдр,[2] который, соответственно, имеет тот же абстрактный вершина фигуры (2 треугольника и два квадрата: 3.4.3.4) и удвоение вершин, ребер и граней. Он имеет ту же топологию, что и абстрактный многогранник полу-кубооктаэдр.
 Кубооктаэдр |  Тетрагемигексаэдр |
Он также может быть выполнен в виде перекрещенного треугольника. куплоид, являясь сокращенной версией {3⁄2} -купола (ретроградный треугольный купол) своим {6⁄2} -гональная база.
| п⁄d | 3 | 5 | 7 |
|---|---|---|---|
| 2 |  Перекрещенный треугольный куплоид |  Пентаграмматический куплоид |  Гептаграмматический куплоид |
| 4 | — |  Перекрещенный пятиугольный куплоид |  Скрещенный гептаграммный куплоид |
Тетрагемигексакрон
| Тетрагемигексакрон | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо | — |
| Элементы | F = 6, E = 12 V = 7 (χ = 1) |
| Группа симметрии | Тd, [3,3], *332 |
| Указатель ссылок | DU04 |
| двойственный многогранник | Тетрагемигексаэдр |
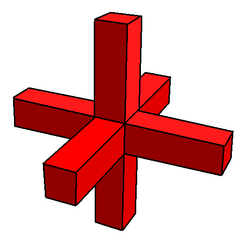
В тетрагемигексакрон это двойной тетрагемигексаэдра и является одним из девяти двойные гемиполиэдры.
Поскольку гемиполиэдры имеют лица проходя через центр, двойные фигуры иметь соответствующие вершины в бесконечности; правильно, на реальная проективная плоскость на бесконечности.[3] В Магнус Веннингер с Двойные модели, они представлены пересекающимися призмы, каждая из которых продолжается в обоих направлениях до одной и той же бесконечно удаленной вершины, чтобы сохранить симметрию. На практике призмы модели обрезаются в удобном для производителя месте. Веннингер предположил, что эти фигуры принадлежат к новому классу людей. звездчатость цифры, называемые звёздчатость до бесконечности. Однако он также предположил, что, строго говоря, они не являются многогранниками, поскольку их конструкция не соответствует обычным определениям.
Топологически считается, что он содержит семь вершин. Три вершины, рассматриваемые на бесконечности ( реальная проективная плоскость на бесконечности) соответствуют трем вершинам полуоктаэдр, абстрактный многогранник. Остальные четыре вершины находятся в разных углах центрального куба (a полукуб, в этом случае тетраэдр ).
Рекомендации
- ^ Медер, Роман. "04: тетрагемигексаэдр". MathConsult.
- ^ а б (Рихтер )
- ^ (Веннингер 2003, п. 101 )
- Рихтер, Дэвид А., Две модели реальной проективной плоскости
- Веннингер, Магнус (2003) [1983], Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, МИСТЕР 0730208 (Стр. 101, Двойники (девяти) гемиполиэдров)
