Усеченный ромбикосододекаэдр - Truncated rhombicosidodecahedron

Усеченный ромбикосододекаэдр

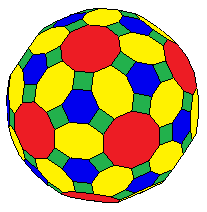Символ Шлефли	trr {5,3} = ${ displaystyle tr { begin {Bmatrix} 5 3 end {Bmatrix}}}$
Обозначение Конвея	taD = baD
Лица	122: 60 {4} 20 {6} 30 {8} 12 {10}
Края	360
Вершины	240
Группа симметрии	я_час, [5,3], (* 532) порядок 120
Группа вращения	Я, [5,3]⁺, (532), заказ 60
Двойной многогранник	Гексеконтаэдр Дисдякиса
Свойства	выпуклый

В геометрия, то усеченный ромбоикосододекаэдр это многогранник, построенный как усеченный ромбикосододекаэдр. У него 122 грани: 12 декагонов, 30 восьмиугольников, 20 шестиугольников и 60 квадратов.

Другие имена

Усеченный малый ромбоикосододекаэдр
Скошенный икосододекаэдр

Зоноэдр

Как зоноэдр, он может быть построен со всеми восьмиугольниками, кроме 30, как правильные многоугольники. Он 2-однородный, с двумя наборами по 120 вершин, существующими на двух расстояниях от его центра.

Этот многогранник представляет собой Сумма Минковского из усеченный икосододекаэдр, а ромбический триаконтаэдр.^[1]

Связанные многогранники

В усеченный икосододекаэдр аналогично, со всеми правильными гранями, и 4.6.10 вершина фигуры. Также см. усеченный ромбикосододекаэдр.

усеченный икосододекаэдр	Усеченный ромбикосододекаэдр
4.6.10	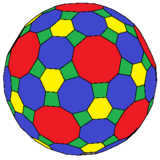4.8.10 и 4.6.8

В усеченный ромбоикосододекаэдр можно увидеть в последовательности исправление и усечение операции из икосододекаэдр. Дальше чередование шаг ведет к курносый ромбикосододекаэдр.

имя	Икозидодека- эдр	Ромб- icosidodeca- эдр	Усеченный ромб icosidodeca- эдр	Курносый ромб icosidodeca- эдр
Coxeter	ID (rD)	rID (rrD)	trID (trrD)	srID (htrrD)
Конвей	объявление	aaD = eD	taaD = baD	грустный
Образ
Конвей	jD	oD	Сумасшедший	ГАД
Двойной