Динамическое равновесие - Dynamic equilibrium

Для использования в других целях см. Динамическое равновесие (значения).

В химия, И в физика, а динамическое равновесие существует однажды обратимая реакция происходит. Вещества переходят между реагентами и продуктами с одинаковой скоростью, что означает отсутствие чистых изменений. Реагенты и продукты образуются с такой скоростью, что их концентрация не меняется. Это частный пример системы в устойчивое состояние. В термодинамика, а закрытая система в термодинамическое равновесие когда реакции происходят с такой скоростью, что состав смеси не меняется со временем. Реакции действительно происходят, иногда бурно, но до такой степени, что изменения в составе невозможно наблюдать. Константы равновесия могут быть выражены через константы скорости обратимых реакций.

Примеры

В новой бутылке газировки концентрация углекислый газ в жидкой фазе имеет особое значение. Если вылить половину жидкости и закрыть бутылку, углекислый газ будет выходить из жидкой фазы с постоянно уменьшающейся скоростью, и частичное давление диоксида углерода в газовой фазе будет увеличиваться до тех пор, пока не будет достигнуто равновесие. В этот момент из-за теплового движения молекула CO₂ может покинуть жидкую фазу, но в течение очень короткого времени другая молекула CO₂ перейдет из газа в жидкость и наоборот. При равновесии скорость переноса CO₂ от газа к жидкой фазе равна скорости перехода от жидкости к газу. В этом случае равновесная концентрация CO₂ в жидкости определяется выражением Закон Генри, который утверждает, что растворимость газа в жидкости прямо пропорциональна частичное давление этого газа над жидкостью.^[1] Это отношение записывается как

${\displaystyle c=kp\,}$

куда k - константа, зависящая от температуры, п парциальное давление и c - концентрация растворенного газа в жидкости. Таким образом, парциальное давление CO₂ газа увеличилось, пока не соблюдается закон Генри. Концентрация углекислого газа в жидкости снизилась, и напиток немного потерял газообразность.

Закон Генри можно вывести, установив химические потенциалы диоксида углерода в двух фазах равны друг другу. Равенство химического потенциала определяет химическое равновесие. Другие константы динамического равновесия, включающие фазовые изменения, включают: Коэффициент распределения и произведение растворимости. Закон Рауля определяет равновесие давление газа из идеальное решение

Динамическое равновесие может существовать и в однофазной системе. Простой пример происходит с кислотно-щелочной равновесие, такое как диссоциация уксусная кислота, в водном растворе.

CH₃CO₂ЧАС ${\displaystyle \rightleftharpoons }$ CH₃CO₂⁻ + H⁺

В состоянии равновесия концентрация частное K, то константа диссоциации кислоты, постоянно (при некоторых условиях)

${\displaystyle K_{c}=\mathrm {\frac {[CH_{3}CO_{2}^{-}][H^{+}]}{[CH_{3}CO_{2}H]}} }$

В этом случае прямая реакция предполагает высвобождение некоторых протоны от молекул уксусной кислоты, и обратная реакция включает образование молекул уксусной кислоты, когда ацетат-ион принимает протон. Равновесие достигается, когда сумма химических потенциалов компонентов в левой части выражения равновесия равна сумме химических потенциалов компонентов в правой части. При этом скорости прямой и обратной реакции равны между собой. Равновесия с образованием химические комплексы также являются динамическими равновесиями, а концентрации регулируются константы устойчивости комплексов.

В газовой фазе также могут возникать динамические равновесия, например, когда диоксид азота димеризуется.

2НО₂ ${\displaystyle \rightleftharpoons }$ N₂О₄; ${\displaystyle K_{p}=\mathrm {\frac {[N_{2}O_{4}]}{[NO_{2}]^{2}}} }$

В газовой фазе квадратные скобки указывают парциальное давление. В качестве альтернативы парциальное давление вещества можно записать как P (вещество).^[2]

Связь между константами равновесия и скоростью

В простой реакции, такой как изомеризация:

${\displaystyle A\rightleftharpoons B}$

необходимо рассмотреть две реакции: прямая реакция, в которой компонент A превращается в B, и обратная реакция, в которой B превращается в A. Если обе реакции элементарные реакции, то скорость реакции дан кем-то^[3]

${\displaystyle {\frac {d[A]}{dt}}=-k_{f}[A]_{t}+k_{b}[B]_{t}}$

куда k_ж это константа скорости для прямой реакции и k_б - константа скорости обратной реакции, квадратные скобки, [..] обозначают концентрация . Если в начале присутствует только A, время т= 0, с концентрацией [A]₀, сумма двух концентраций, [A]_т и [B]_т, вовремя т, будет равно [A]₀.

${\displaystyle {\frac {d[A]}{dt}}=-k_{f}[A]_{t}+k_{b}\left([A]_{0}-[A]_{t}\right)}$

% концентрации частиц в реакции изомеризации. k_ж = 2 с⁻¹, k_р = 1 с⁻¹

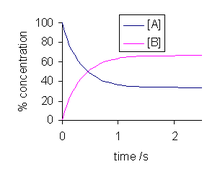
Решение этого дифференциального уравнения есть

${\displaystyle [A]_{t}={\frac {k_{b}+k_{f}e^{-\left(k_{f}+k_{b}\right)t}}{k_{f}+k_{b}}}[A]_{0}}$

и показан справа. Когда время стремится к бесконечности, концентрации [A]_т и [B]_т стремятся к постоянным значениям. Позволять т приближаются к бесконечности, то есть т→ ∞ в приведенном выше выражении:

${\displaystyle [A]_{\infty }={\frac {k_{b}}{k_{f}+k_{b}}}[A]_{0};[B]_{\infty }={\frac {k_{f}}{k_{f}+k_{b}}}[A]_{0}}$

На практике изменения концентрации невозможно измерить после ${\displaystyle t\gtrapprox {\frac {10}{k_{f}+k_{b}}}}$. Поскольку после этого концентрации не меняются, они определение, равновесные концентрации. Теперь константа равновесия для реакции определяется как

${\displaystyle K={\frac {[B]_{eq}}{[A]_{eq}}}}$

Отсюда следует, что константа равновесия численно равна отношению констант скорости.

${\displaystyle K={\frac {{\frac {k_{f}}{k_{f}+k_{b}}}[A]_{0}}{{\frac {k_{b}}{k_{f}+k_{b}}}[A]_{0}}}={\frac {k_{f}}{k_{b}}}}$

Как правило, это может быть более одной прямой реакции и более одной обратной реакции. Аткинс заявляет^[4] что для общей реакции общая константа равновесия связана с константами скорости элементарных реакций соотношением

${\displaystyle K=\left({\frac {k_{f}}{k_{b}}}\right)_{1}\times \left({\frac {k_{f}}{k_{b}}}\right)_{2}\dots }$ .

Смотрите также

• Равновесная химия
• Механическое равновесие
• Химическое равновесие
• Радиационное равновесие

Рекомендации

Аткинс, P.W .; де Паула, Дж. (2006). Физическая химия (8-е изд.). Издательство Оксфордского университета. ISBN  0-19-870072-5.

1. Аткинс, Раздел 5.3
2. Денби, К. (1981). Принципы химического равновесия (4-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-28150-4.
3. Аткинс, Раздел 22.4
4. Аткинс, Раздел 22.4

внешняя ссылка

• http://demonstrations.wolfram.com/DynamicEquilibriumExample/