Глубина удара - Impact depth
Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. (Ноябрь 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Физик сэр Исаак Ньютон впервые разработал эту идею для получения грубых приближений глубина удара за снаряды движущиеся с высокими скоростями.
Приближение Ньютона для глубины удара
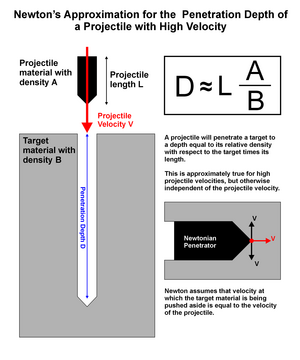
Приближение Ньютона для глубины удара снарядов на высоких скоростях основано только на импульс соображения. Ничего не сказано о том, где находится ударник. кинетическая энергия идет, ни что происходит с импульсом после остановки снаряда.
Основная идея проста: ударный элемент передает заданный импульс. Чтобы остановить ударник, этот импульс необходимо передать другой массе. Поскольку скорость ударника настолько велика, что сплоченность внутри материала мишени можно пренебречь, импульс может быть передан только материалу (массе) непосредственно перед ударником, который будет толкаться со скоростью ударника. Если ударный элемент толкнул массу, равную его собственной массе, с этой скоростью, весь его импульс будет передан массе перед ним, и ударный элемент будет остановлен. В случае цилиндрического ударного элемента к моменту остановки он проникнет на глубину, равную его собственной длине, умноженной на его относительную плотность по отношению к материалу мишени.
Этот подход применим только для тупого ударника (без аэродинамической формы) и материала мишени с нет волокон (нет сцепления), по крайней мере, не со скоростью ударника. Обычно это верно, если скорость ударника намного выше скорости звука в материале цели. При таких высоких скоростях большинство материалов начинают вести себя как жидкость. В этом случае важно, чтобы снаряд оставался компактной во время удара (не разлетался).
Приложения
- Снаряд: Цельнометаллические снаряды должны быть сделаны из материала с очень высокой плотностью, например урана (19,1 г / см3) или свинец (11,3 г / см3). Согласно приближению Ньютона, цельнометаллический снаряд, сделанный из урана, пробьет стальную броню примерно в 2,5 раза больше ее собственной длины.
- Формованный заряд, базука: Для того, чтобы кумулятивный заряд (противотанковый) пробил стальные пластины, важно, чтобы взрыв генерировал длинную струю тяжелого металла (в кумулятивном заряде для противотанкового применения взрыв генерирует высокоскоростную струю металла из конуса фасонная металлическая футеровка). Тогда эту струю можно рассматривать как ударник приближения Ньютона.
- Метеорит: Как можно заключить по давлению воздуха, материал атмосферы эквивалентен примерно 10 м воды. Поскольку лед имеет примерно такую же плотность, что и вода, кубик льда из космоса, движущийся со скоростью 15 км / с или около того, должен иметь длину 10 м, чтобы достичь поверхности земли с высокой скоростью. Меньший кубик льда остановится в воздухе и взорвется. Однако кубик льда диаметром 50 м и более также может быть остановлен в воздухе, если он входит под очень малым углом и, следовательно, должен проходить сквозь большую часть атмосферы. В Тунгусское событие иногда так объясняют. Железный метеорит длиной 1,3 м пробьет атмосферу; меньший будет замедлен в воздухе и упадет на предельная скорость на землю.
- Импактор, бункер: Вместо ядерных боеголовок для проникновения бункеры глубоко под землей. Согласно приближению Ньютона, урановый снаряд на высокой скорости и длиной 1 м пробьет 6 м породы (плотность 3 г / см3) перед тем, как остановиться.
Смотрите также
дальнейшее чтение
- Янг, C.W. (1967). Разработка эмпирических уравнений для прогнозирования глубины полета снаряда, проникающего через землю (Отчет). SC-DR-67-60. Альбукерке, штат Нью-Мексико: Sandia National Laboratories.CS1 maint: ref = harv (связь)
- Янг, C.W. (1997). Уравнения проникновения (PDF) (Отчет). SAND94-2726. Альбукерке, Нью-Мексико: Сандийские национальные лаборатории.
Это отдельный отчет, в котором задокументирована последняя обновленная версия уравнений проникновения Янга / Сандиа и связанные с ними аналитические методы для прогнозирования проникновения в природные грунтовые материалы и бетон. См. Приложение A и B для ознакомления с уравнениями проникновения.
CS1 maint: ref = harv (связь) - Алексеевский, В. П. (1966). «Проникновение стержня в цель на большой скорости». Горение, взрыв и ударные волны (Физика Горения и Взрыва). 2 (2): 99–106. Дои:10.1007 / BF00749237. ISSN 0010-5082.
- Тейт, А. (1 ноября 1967 г.). "Теория замедления длинных стержней после удара" (PDF). Журнал механики и физики твердого тела. 15 (6): 387–399. Bibcode:1967JMPSo..15..387T. Дои:10.1016/0022-5096(67)90010-5. Архивировано из оригинал (PDF) 26 марта 2012 г.. Получено 23 июн 2011.
- Бернард, Роберт С. (1978). Прогнозирование глубины и движения проникающих через землю (PDF) (Отчет). ADA056701. Виксбург, штат Массачусетс: Инженер армии, экспериментальная станция водных путей Виксбург.CS1 maint: ref = harv (связь)
- Уолтерс, Уильям П .; Сеглетес, Стивен Б. (1991). «Точное решение уравнений проникновения длинного стержня». Международный журнал ударной инженерии. 11 (2): 225–231. Дои:10.1016 / 0734-743X (91) 90008-4.
- Segletes, Стивен Б .; Уолтерс, Уильям П. (2002). Эффективное решение уравнений проникновения длинного стержня Алексеевского-Тейта. (PDF) (Отчет). ARL-TR-2855. Абердин, Мэриленд: Армейская исследовательская лаборатория Абердинский испытательный полигон.CS1 maint: ref = harv (связь)
- Segletes, Стивен Б .; Уолтерс, Уильям П. (2003). "Расширения к точному решению уравнений проникновения / эрозии длинного стержня" (PDF). Международный журнал ударной инженерии. 28 (4): 363–376. Дои:10.1016 / S0734-743X (02) 00071-4. Получено 23 июн 2011.
