Колыбель Ньютона - Newtons cradle - Wikipedia
Эта статья нужны дополнительные цитаты для проверка. (Август 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В Колыбель Ньютона это устройство, которое демонстрирует сохранение импульса и энергия используя серию качающихся сфер. Когда одна сфера в конце поднимается и отпускается, она ударяется о неподвижный сферы, передавая силу через неподвижные сферы, которая толкает последнюю сферу вверх. Последняя сфера отскакивает назад и ударяет по еще почти неподвижным сферам, повторяя эффект в противоположном направлении. Устройство названо в честь 17-го века английский ученый Сэр Исаак Ньютон. Он также известен как Маятник Ньютона, Шары Ньютона, Рокер Ньютона или же исполнительный мяч кликер (поскольку устройство издает щелчок каждый раз, когда шары сталкиваются, что происходит неоднократно в стабильном ритме).[1][2]

Типичная колыбель Ньютона состоит из серии металлических шариков одинакового размера, подвешенных в металлической раме, так что в состоянии покоя они просто касаются друг друга.
Операция
Когда один из концевых шариков («первый») тянется в сторону, прикрепленная струна заставляет его двигаться по восходящей дуге. Когда его отпускают, он ударяет по второму мячу и почти полностью останавливается. Мяч на противоположной стороне приобретает большую часть скорости первого шара и совершает поворот по дуге, почти равной высоте высвобождения первого шара. Это показывает, что последний шар получает большую часть энергии и импульса первого шара. Удар вызывает волну сжатия, которая распространяется через промежуточные шары. Это делает любой эффективно эластичный материал, такой как сталь, при условии, что кинетическая энергия временно сохраняется в виде потенциальной энергии при сжатии материала, а не теряется в виде тепла. После первоначального удара все шары совершают небольшие движения, но последний шар получает большую часть начальной энергии от удара первого шара. Когда два (или три) шара выпадают, два (или три) шара на противоположной стороне выходят наружу. Некоторые говорят, что такое поведение демонстрирует сохранение импульса и кинетической энергии при упругих столкновениях. Однако, если сталкивающиеся шары ведут себя, как описано выше, с одинаковой массой, обладающей одинаковой скоростью до и после столкновений, то в таком случае сохраняется любая функция массы и скорости.[3]
Объяснение физики

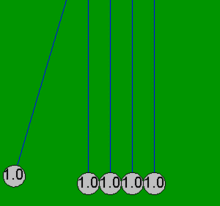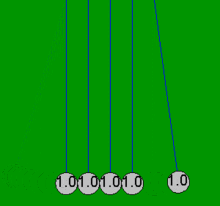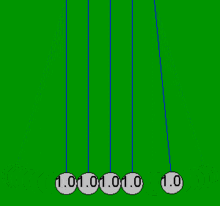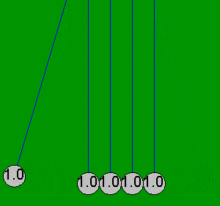
Колыбель Ньютона можно довольно точно смоделировать с помощью простых математических уравнений в предположении, что шары всегда сталкиваются попарно. Если один шар сталкивается с четырьмя неподвижными шарами, которые уже касаются друг друга, эти простые уравнения не могут объяснить результирующие движения всех пяти шаров, которые не связаны с потерями на трение. Например, в настоящей колыбели Ньютона четвертый шар имеет некоторое движение, а первый шар - немного обратное движение. Все анимации в этой статье демонстрируют идеализированное действие (простое решение), которое происходит только в том случае, если шары нет касаются сначала и сталкиваются только парами.
Простое решение
Сохранение импульса (масса × скорость) и кинетическая энергия (1/2 × масса × скорость2) можно использовать для нахождения результирующих скоростей для два сталкивающихся идеально упругих объекта. Эти два уравнения используются для определения результирующих скоростей двух объектов. В случае двух шаров, ограниченных прямой траекторией струнами в люльке, скорости представляют собой одно число, а не трехмерный вектор для трехмерного пространства, поэтому математика требует только двух уравнений для решения двух неизвестных. Когда два объекта весят одинаково, решение простое: движущийся объект останавливается относительно неподвижного, а неподвижный объект набирает начальную скорость всего другого. Это предполагает идеально упругие объекты, поэтому нет необходимости учитывать потери тепловой и звуковой энергии.
Сталь не сильно сжимается, но ее эластичность очень эффективна, поэтому она не вызывает большого отходящее тепло. Простой эффект от двух эффективно эластичных сталкивающихся объектов одинакового веса, ограниченных прямым путем, является основой эффекта, наблюдаемого в люльке, и дает приблизительное решение для всех его действий.
Для последовательности упругих объектов одинакового веса, ограниченных прямым путем, эффект распространяется на каждый последующий объект. Например, когда два шара падают, чтобы поразить три неподвижных шара в люльке, существует незаметное, но решающее небольшое расстояние между двумя выпавшими шарами, и действие выглядит следующим образом: первый движущийся шар, который ударяет первый неподвижный шар ( второй шар ударяет третий шар) передает всю свою скорость третьему шару и останавливается. Затем третий шар передает скорость четвертому шару и останавливается, а затем четвертый шар - пятому. Сразу за этой последовательностью находится второй движущийся шар, передающий свою скорость первому движущемуся шару, который только что остановился, и последовательность повторяется немедленно и незаметно после первой последовательности, выбрасывая четвертый шар сразу за пятым шаром с таким же небольшим расстоянием между два начальных ударных шара. Если они просто касаются третьего мяча, точность требует более полного решения, приведенного ниже.
Другие примеры этого эффекта
Эффект выброса последнего шара со скоростью, почти равной скорости первого шара, можно увидеть в скольжении монеты по столу в ряд одинаковых монет, пока поражающая монета и ее двойные цели находятся на прямой линии. Аналогичным образом эффект можно увидеть в бильярдных шарах. Эффект также можно увидеть, когда резкая и сильная волна давления ударяет по плотному однородному материалу, погруженному в менее плотную среду. Если идентичные атомы, молекулы или более крупномасштабные подобъемы плотного однородного материала хотя бы частично упруго связаны друг с другом электростатическими силами, они могут действовать как последовательность сталкивающихся идентичных упругих шаров. Окружающие атомы, молекулы или частичные объемы, испытывающие волну давления, действуют, сдерживая друг друга, подобно тому, как струна удерживает шары люльки на прямой линии. Например, литотрипсия ударные волны могут проходить через кожу и ткани без вреда для взрыва камни в почках. Сторона камней, противоположная набегающей волне давления, лопается, а не сторона, получившая первоначальный удар.
Когда применяется простое решение
В простом решении для точного прогнозирования действия ни одна пара в процессе столкновения не может коснуться третьего шара, потому что присутствие третьего шара фактически делает пораженный шар более тяжелым. Применение двух уравнений сохранения для определения конечных скоростей трех или более шаров в одном столкновении приводит к множеству возможных решений, поэтому этих двух принципов недостаточно для определения результирующего действия.
Даже при небольшом начальном разделении, третий шар может участвовать в столкновении, если начальное разделение недостаточно велико. В этом случае необходимо использовать метод полного решения, описанный ниже.
Маленькие стальные шарики работают хорошо, потому что они остаются эффективно эластичными с небольшими потерями тепла при сильных ударах и не сильно сжимаются (примерно до 30 мкм в маленькой колыбели Ньютона). Небольшие жесткие сжатия означают, что они происходят быстро, менее чем за 200 микросекунд, поэтому стальные шары с большей вероятностью завершат столкновение до того, как коснутся ближайшего третьего шара. Более мягкие эластичные шары требуют большего расстояния для максимального эффекта от парных столкновений.
Более полное решение

Колыбель, которая лучше всего соответствует простому решению, должна иметь начальное расстояние между шариками, которое, по крайней мере, в два раза больше, чем сжимается любой шарик, но в большинстве случаев этого не происходит. В этом разделе описываются действия, когда начального разделения недостаточно, а также при последующих столкновениях, в которых участвует более двух шаров, даже при начальном разделении. Это решение упрощается до простого решения, когда только два шара касаются во время столкновения. Это применимо ко всем идеально эластичным идентичным шарам, которые не имеют потерь энергии из-за трения и могут быть аппроксимированы такими материалами, как сталь, стекло, пластик и резина.
При столкновении двух шаров для решения двух неизвестных результирующих скоростей необходимы только два уравнения сохранения импульса и энергии. Для трех или более одновременно сталкивающихся упругих шаров относительная сжимаемость сталкивающихся поверхностей является дополнительными переменными, которые определяют результат. Например, пять шаров имеют четыре точки столкновения, и масштабирование (деление) трех из них на четвертое дает три дополнительные переменные, необходимые для решения всех пяти скоростей после столкновения.
Ньютонов, лагранжиан, гамильтониан и стационарное действие - это разные способы математического выражения классической механики. Они описывают одну и ту же физику, но должны решаться разными методами. Все обеспечивают сохранение энергии и импульса. Закон Ньютона использовался в исследовательских работах. Он применяется к каждому мячу, и сумма сил приравнивается к нулю. Итак, есть пять уравнений, по одному для каждого шара, и пять неизвестных, по одному для каждой скорости. Если шары идентичны, абсолютная сжимаемость поверхностей не имеет значения, потому что ее можно разделить на обе части всех пяти уравнений, получив ноль.
Определение скоростей[4][5][6] для случая, когда один шар ударяет по четырем первоначально касающимся шарам, можно найти, моделируя шары как грузы с нетрадиционными пружинами на их сталкивающихся поверхностях. Большинство материалов, таких как сталь, которые являются эффективно эластичными, приблизительно подчиняются закону силы Гука для пружин, , но поскольку площадь контакта для сферы увеличивается с увеличением силы, сталкивающиеся упругие шары следуют поправке Герца к закону Гука, . Это и закон движения Ньютона () применяются к каждому шару, давая пять простых, но взаимозависимых дифференциальных уравнений, которые решаются численно. Когда пятый шар начинает ускоряться, он получает импульс и энергию от третьего и четвертого шариков за счет пружинящего действия их сжатых поверхностей. Для идентичных эластичных мячей любого типа с изначально касающимися шарами действие при первом ударе одинаково, за исключением того, что время до завершения столкновения увеличивается в более мягких материалах. От 40% до 50% кинетической энергии исходного мяча от удара одиночным мячом хранится на поверхностях шара в качестве потенциальной энергии для большей части процесса столкновения. Четвертому шару передается 13 процентов начальной скорости (что можно рассматривать как движение на 3,3 градуса, если пятый шар перемещается на 25 градусов), и у первых трех шаров наблюдается небольшая обратная скорость, причем первый шар имеет самый большой при −7% от начальной скорости. Это разделяет шары, но они возвращаются вместе непосредственно перед возвращением пятого шара. Это происходит из-за явления маятника, когда разные возмущения под небольшим углом имеют примерно одинаковое время, чтобы вернуться в центр. Когда шары "касаются" при последующих столкновениях, это сложно, но все же можно определить этим методом, особенно если включены потери на трение и время маятника рассчитывается точно, а не полагаться на приближение малых углов.
Дифференциальные уравнения с начальным разделением необходимы, если расстояние менее 10 мкм при использовании 100-граммовых стальных шаров с начальной скоростью удара 1 м / с.
Дифференциальные уравнения Герца предсказывают, что если два шара ударится по трем, пятый и четвертый шары улетят со скоростями, в 1,14 и 0,80 раз превышающими начальную скорость.[7] Это в 2,03 раза больше кинетической энергии в пятом шаре, чем в четвертом шаре, что означает, что пятый шар будет качаться в вертикальном направлении вдвое выше, чем четвертый шар. Но в настоящей колыбели Ньютона четвертый шар улетает до пятого шара. Чтобы объяснить разницу между теорией и экспериментом, два поражающих шара должны иметь расстояние не менее ≈10 мкм (для стали, 100 г и 1 м / с). Это показывает, что в обычном случае стальных шариков незамеченные разделения могут быть важны и должны быть включены в дифференциальные уравнения Герца, иначе простое решение даст более точный результат.
Влияние волн давления
Предполагалось, что силы в вышеприведенном решении Герца немедленно распространяются в шарах, что не соответствует действительности. Внезапные изменения силы между атомами материала создают волну давления. Волны давления (звук) в стали проходят около 5 см за 10 микросекунд, что примерно в 10 раз быстрее, чем время между первым ударом шара и последним выбросом шара. Волны давления отражаются назад и вперед через все пять шаров примерно десять раз, хотя и рассеиваются на меньшую часть волнового фронта с большим количеством отражений. Это достаточно быстро, чтобы решение Герца не требовало существенной модификации для корректировки задержки распространения силы через шары. В менее жестких, но все же очень эластичных шарах, таких как резина, скорость распространения меньше, но продолжительность столкновений больше, поэтому решение Герца все еще применимо. Ошибка, вызванная ограниченной скоростью распространения силы, смещает решение Герца в сторону простого решения, поскольку на столкновения не так сильно влияет инерция более удаленных шаров.
Шары идентичной формы помогают волнам давления сходиться в точке контакта последнего шара: в точке первоначального удара одна волна давления идет вперед к другим шарам, а другая движется назад, отражаясь от противоположной стороны первого шара, а затем он следует за первой волной, отстав от нее ровно на 1 диаметр шара. Две волны встречаются в последней точке контакта, потому что первая волна отражается от противоположной стороны последнего шара и встречается в последней точке контакта со второй волной. Затем они отражаются взад и вперед примерно 10 раз, пока первый шар не перестанет соединяться со вторым шаром. Затем реверберации отражаются от точки контакта между вторым и третьим шарами, но по-прежнему сходятся в последней точке контакта, пока последний шар не будет выброшен - но с каждым отражением это меньше волнового фронта.
Влияние разных типов мячей
Использование различных типов материалов не меняет действия, пока материал эффективно эластичен. Размер сфер не влияет на результаты, если увеличенный вес не превышает предел упругости материала. Если твердые шары слишком большие, энергия теряется в виде тепла, потому что предел упругости увеличивается с увеличением радиуса до степени 1,5, но энергия, которая должна быть поглощена и высвобождена, увеличивается как куб радиуса. Сделав контактные поверхности более плоскими, можно до некоторой степени решить эту проблему, распределяя сжатие на большее количество материала, но это может вызвать проблемы с выравниванием. Сталь лучше, чем большинство материалов, потому что она позволяет простому решению чаще применяться при столкновениях после первого удара, ее диапазон упругости для сохранения энергии остается хорошим, несмотря на более высокую энергию, вызванную ее весом, а более высокий вес снижает эффект сопротивления воздуха. .
Потери тепла и трения
В этом обсуждении не учитывались потери энергии из-за тепла, выделяемого в шарах из-за неидеальной упругости, трения в струнах, трения из-за сопротивления воздуха и звука, генерируемого лязгом колеблющихся шаров. Потери энергии являются причиной того, что шары в конечном итоге останавливаются, но они не являются основной или исходной причиной того, что действие становится более беспорядочным, в отличие от идеального действия только одного шара, движущегося в любой момент. Увеличение неидеального действия вызвано столкновениями, в которых участвуют более двух шаров одновременно, что фактически делает пораженный шар более тяжелым. Размер стальных шариков ограничен, потому что столкновения могут превышать предел упругости стали, деформируя ее и вызывая потери тепла.
Приложения
Наиболее распространенное приложение - настольный компьютер. исполнительная игрушка. Другое использование - как учебная демонстрация физики, как пример сохранение импульса и сохранение энергии.
Похожий принцип - распространение волн в твердых телах - использовался в Константинеско. Шестерня синхронизации система синхронизаторов пропеллера и пушки на ранних истребителях.[требуется дальнейшее объяснение ]
История

Кристиан Гюйгенс использовали маятники для изучения столкновений. Его работа, De Motu Corporum ex Percussione (О движении тел при столкновении), опубликованная посмертно в 1703 году, содержит версию Первый закон Ньютона и обсуждает столкновение подвешенных тел, включая два тела одинаковой массы, при этом движение движущегося тела передается одному неподвижному.
Принцип, продемонстрированный устройством, закон соударений между телами, был впервые продемонстрирован французами. физик Аббат Мариотт в 17 веке.[1][8] Ньютон признал работу Мариотта, среди прочих, в его Principia.
Существует много недоразумений относительно происхождения современной колыбели Ньютона. Мариус Дж. Морин считается первым, кто назвал и сделал это популярным исполнительная игрушка.[нужна цитата ] Однако в начале 1967 года английский актер, Саймон Преббл, придумал название «колыбель Ньютона» (в настоящее время используется в общем) для деревянной версии, произведенной его компанией Scientific Demonstrations Ltd.[9] После некоторого первоначального сопротивления со стороны розничных продавцов они были сначала проданы Harrods Лондона, тем самым положив начало устойчивому рынку игрушек для руководителей.[нужна цитата ] Позже скульптор и будущий кинорежиссер создал очень удачный хромированный дизайн для магазина Gear на Карнаби-стрит. Ричард Лонкрэйн.[нужна цитата ]
Самая большая подставка в мире была разработана Разрушители легенд и состоял из пяти тонных бетона и стали арматура -наполненные буи, подвешенные к стальной ферме.[10] Между двумя половинами буев также была вставлена стальная пластина, которая служила «точкой контакта» для передачи энергии; это устройство люльки не функционировало должным образом, потому что бетон неэластичен, поэтому большая часть энергии была потеряна на накопление тепла в бетоне. Созданная ими версия меньшего масштаба состоит из пяти 15-сантиметровых (6 дюймов) шарикоподшипников из хромистой стали, каждый весит 15 кг (33 фунта), и по эффективности почти не уступает настольной модели.
Колыбель с шарами столкновения самого большого диаметра на всеобщем обозрении был виден более года в Милуоки, Висконсин, в розничном магазине American Science and Surplus (см. Фото). Каждый мяч представлял собой надувной мяч для упражнений диаметром 66 см (26 дюймов) (заключенный в стальные кольца) и поддерживался от потолка с помощью чрезвычайно сильных магнитов. Он был разобран в начале августа 2010 года из-за проблем с ремонтом.[нужна цитата ]
В популярной культуре
Колыбель Ньютона более 20 раз использовалась в кино,[11] часто как троп на столе главного злодея, такого как роль Пола Ньюмана в Прокси-сервер Hudsucker, Магнето в Люди Икс, а криптонианцы в Супермен 2. Он использовался, чтобы обозначить непреклонную позицию НФЛ в отношении травм головы в Сотрясение.[12] Он также использовался в качестве расслабляющего развлечения на столе для ведущих умных / тревожных / чувствительных персонажей, таких как роль Генри Винклера в Ночная смена, Дастин Хоффман роль в Соломенные псы, и Гвинет Пэлтроу роль в Железный Человек 2. Это было более заметно как серия глиняных горшков в Розенкранц и Гильденстерн мертвы, а как ряд 1968 г. Ээро Аарнио пузырьковые стулья с полураздетыми женщинами в них. Геймер.[13] В Аисты У Хантера, генерального директора Cornerstore, есть один не с шариками, а с птичками.
В 2017 г. вышел эпизод Омнибус подкаст, с участием Опасность! чемпион Кен Дженнингс и музыкант Джон Родерик, посвященный истории Колыбели Ньютона.[14] Колыбель Ньютона также находится на столе заместителя директора по коммуникациям Белого дома. Сэм Сиборн в Западное крыло.
Рок-группа Джефферсон Самолет использовал колыбель на альбоме 1968 года Корона творения как ритм-устройство для создания полиритмы на инструментальной композиции.
Смотрите также
Рекомендации
- ^ а б "Колыбель Ньютона". Демонстрации лекций по естественным наукам в Гарварде. Гарвардский университет. 27 февраля 2019.
- ^ Палермо, Элизабет (28 августа 2013 г.). «Как работает колыбель Ньютона?». Живая наука.
- ^ Голд, Колин Ф. (август 2006 г.). "Колыбель Ньютона в физическом образовании". Научное образование. 15 (6): 597–617. Bibcode:2006Sc & Ed..15..597G. Дои:10.1007 / s11191-005-4785-3.
- ^ Herrmann, F .; Зейтц, М. (1982). "Как работает шариковая цепь?" (PDF). Американский журнал физики. 50. С. 977–981. Bibcode:1982AmJPh..50..977H. Дои:10.1119/1.12936.
- ^ Lovett, D. R .; Молдинг, К. М .; Анкетелл-Джонс, С. (1988). «Столкновения упругих тел: колыбель Ньютона». Европейский журнал физики. 9 (4): 323. Bibcode:1988EJPh .... 9..323L. Дои:10.1088/0143-0807/9/4/015.
- ^ Хутцлер, Стефан; Делани, Гэри; Уир, Денис; МакЛауд, Финн (2004). "Качающаяся колыбель Ньютона" (PDF). Американский журнал физики. 72. С. 1508–1516. Bibcode:2004AmJPh..72.1508H. Дои:10.1119/1.1783898.К. Ф. Голд (2006), колыбель Ньютона в физическом образовании, Научное образование, 15, 597-617
- ^ Hinch, E.J .; Сен-Жан, С. (1999). «Разрыв шаров в результате удара» (PDF). Proc. R. Soc. Лондон. А. 455. С. 3201–3220.
- ^ Wikisource: Католическая энциклопедия (1913) / Эдме Мариотт
- ^ Шульц, Крис (17 января 2012 г.). "Как работают колыбели Ньютона". Как это работает. Получено 27 февраля 2019.
- ^ «Колыбель Ньютона (5 октября 2011 г.)» на IMDb
- ^ Самые популярные названия "Колыбель Ньютона" - IMDb
- ^ Сотрясение мозга - Обзоры Cinemaniac В архиве 11 февраля 2017 года в Wayback Machine
- ^ 13 икон современного дизайна в фильмах «Основы стиля»
- ^ Омнибус: Колыбель Ньютона (Запись 835.1C1311)
Литература
- Херрманн, Ф. (1981). «Простое объяснение известного эксперимента со столкновениями». Американский журнал физики. 49 (8): 761. Bibcode:1981AmJPh..49..761H. Дои:10.1119/1.12407.
- Б. Брольято: Негладкая механика. Модели, динамика и управление, Springer, 2-е издание, 1999 г.




