Теорема Ньютона о вращающихся орбитах - Newtons theorem of revolving orbits - Wikipedia

Воспроизвести медиа

Рисунок 1: Сила притяжения F(р) заставляет голубую планету двигаться по голубому кругу. Зеленая планета движется в три раза быстрее и поэтому требует более сильного центростремительная сила, который обеспечивается добавлением притягивающей силы обратного куба. Красная планета неподвижна; сила F(р) уравновешивается отталкивающей силой обратного куба. А Гифка версия этой анимации найдена здесь.

Рисунок 2: Радиус р зеленых и синих планет одинаковы, но их угловая скорость отличается в разы k. Примеры таких орбит показаны на рисунках 1 и 3–5.

В классическая механика, Теорема Ньютона о вращающихся орбитах определяет тип центральная сила необходимо умножить угловая скорость частицы на фактор k не влияя на его радиальное движение (рисунки 1 и 2). Ньютон применил свою теорему к пониманию общего вращения орбит (апсидальная прецессия, Рис.3), что наблюдается для Луна и планеты. Термин «радиальное движение» означает движение к центру силы или от него, тогда как угловое движение перпендикулярно радиальному движению.

Исаак Ньютон вывел эту теорему в предложениях 43–45 книги I его Philosophiæ Naturalis Principia Mathematica, впервые опубликовано в 1687 году. В предложении 43 он показал, что добавленная сила должна быть центральной силой, величина которой зависит только от расстояния р между частицей и точкой, закрепленной в пространстве (центром). В предложении 44 он вывел формулу для силы, показав, что это сила обратного куба, изменяющаяся как обратный куб р. В предложении 45 Ньютон распространил свою теорему на произвольные центральные силы, предположив, что частица движется по почти круговой орбите.

Как отмечает астрофизик Субраманян Чандрасекар в его комментариях 1995 г. Principia, эта теорема оставалась в значительной степени неизвестной и неразработанной более трех столетий.^[1] С 1997 г. теорему изучают Дональд Линден-Белл и сотрудники.^[2][3] Его первое точное расширение произошло в 2000 году благодаря работе Магомеда и Вавды.^[4]

Исторический контекст

Ретроградное движение Марс если смотреть с Земли.

Воспроизвести медиа

Рисунок 3: Планеты, вращающиеся вокруг Солнца, движутся по эллиптическим (овальным) орбитам, которые постепенно со временем вращаются (апсидальная прецессия). В эксцентриситет этого эллипса увеличено для визуализации. Большинство орбит в Солнечной системе имеют гораздо меньший эксцентриситет, что делает их почти круглыми. А Гифка версия этой анимации найдена здесь.

Движение астрономических тел систематически изучается на протяжении тысяч лет. Было замечено, что звезды вращаются равномерно, всегда сохраняя одно и то же положение относительно друг друга. Однако было замечено, что другие тела бродить на фоне неподвижных звезд; большинство таких тел были названы планеты после греческого слова «πλανήτοι» (Planētoi) для "странников". Хотя обычно они движутся в одном и том же направлении по небу ( эклиптика ), отдельные планеты иногда на короткое время меняют свое направление, показывая ретроградное движение.^[5]

Чтобы описать это движение вперед и назад, Аполлоний Пергский (c. 262 - с. 190 г. до н.э.) разработал концепцию семявыносящие протоки и эпициклы, согласно которому планеты перемещаются по вращающимся кругам, которые сами перемещаются по другим вращающимся кругам, и так далее. Любую орбиту можно описать с помощью достаточного количества разумно выбранных эпициклов, поскольку такой подход соответствует современному преобразование Фурье.^[6] Примерно 350 лет спустя Клавдий Птолемей опубликовал свой Альмагест, в котором он разработал эту систему, чтобы соответствовать лучшим астрономическим наблюдениям его эпохи. Для объяснения эпициклов Птолемей принял геоцентрический космология Аристотель, согласно которому планеты были ограничены концентрическими вращающимися сферами. Эта модель вселенная был авторитетным почти 1500 лет.

Современное понимание движения планет возникло в результате совместных усилий астронома. Тихо Браге и физик Иоганн Кеплер в 16 веке. Тихо приписывают чрезвычайно точные измерения движения планет, из которых Кеплер смог получить свои законы движения планет.^[7] По этим законам планеты движутся дальше эллипсы (нет эпициклы ) о солнце (не Земля). Второй и третий законы Кеплера делают конкретные количественные предсказания: планеты охватывают равные площади за равное время, и квадрат их орбитальные периоды равна фиксированной константе, умноженной на куб их большая полуось.^[8] Последующие наблюдения планетных орбит показали, что длинная ось эллипса (так называемая линия апсид) постепенно вращается со временем; это вращение известно как апсидальная прецессия. В апсиды орбиты - это точки, в которых вращающееся тело наиболее близко или дальше всего от притягивающего центра; для планет, вращающихся вокруг Солнца, апсиды соответствуют перигелию (ближайшему) и афелию (самому дальнему).^[9]

С публикацией его Principia примерно восемьдесят лет спустя (1687 г.), Исаак Ньютон предоставил физическую теорию, объясняющую все три закона Кеплера, теорию, основанную на Законы движения Ньютона и его закон всемирного тяготения. В частности, Ньютон предположил, что гравитационная сила между любыми двумя телами была центральная сила F(р), которые варьировались как обратный квадрат расстояния р между ними. Основываясь на своих законах движения, Ньютон показал, что орбита любой частицы, на которую действует одна такая сила, всегда коническая секция, особенно эллипс, если он не уходит в бесконечность. Однако этот вывод верен только при наличии двух тел ( проблема двух тел ); движение трех или более тел, действующих под действием их взаимного тяготения ( ппроблема тела ) оставался нерешенным в течение столетий после Ньютона,^[10][11] хотя решения некоторых Особые случаи были обнаружены.^[12] Ньютон предположил, что орбиты планет вокруг Солнца в основном эллиптические, потому что гравитация Солнца является доминирующей; к первое приближение, присутствие других планет можно не учитывать. По аналогии, эллиптическая орбита Луна около Земли преобладала сила тяжести Земли; в первом приближении гравитацией Солнца и других тел Солнечной системы можно пренебречь. Однако Ньютон заявил, что постепенная апсидальная прецессия планетных и лунных орбит была вызвана эффектами этих игнорируемых взаимодействий; в частности, он заявил, что прецессия орбиты Луны была вызвана возмущающими эффектами гравитационного взаимодействия с Солнцем.^[13]

Теорема Ньютона о вращающихся орбитах была его первой попыткой количественно понять прецессию апсид. Согласно этой теореме, добавление особого типа центральной силы - силы обратного куба - может создать вращающуюся орбиту; угловая скорость умножается на коэффициент k, а радиальное движение не изменилось. Однако эта теорема ограничена определенным типом силы, которая может не иметь значения; несколько возмущающих взаимодействий обратных квадратов (например, на других планетах) кажутся маловероятными в сумме в точности с силой обратного куба. Чтобы применить свою теорему к другим типам сил, Ньютон нашел наилучшее приближение произвольной центральной силы. F(р) к потенциалу обратного куба в пределе почти круговых орбит, то есть эллиптических орбит с низким эксцентриситетом, что действительно верно для большинства орбит в Солнечной системе. Чтобы найти это приближение, Ньютон разработал бесконечный ряд, который можно рассматривать как предшественника Расширение Тейлора.^[14] Это приближение позволило Ньютону оценить скорость прецессии для произвольных центральных сил. Ньютон применил это приближение к тестовым моделям силы, вызывающей апсидальную прецессию орбиты Луны. Однако проблема движения Луны пугающе сложна, и Ньютон никогда не публиковал точную гравитационную модель апсидальной прецессии Луны. После более точной модели Clairaut в 1747 г.,^[15] аналитические модели движения Луны были разработаны в конце 19 века. холм,^[16] Коричневый,^[17] и Делоне.^[18]

Однако теорема Ньютона является более общей, чем просто объяснение прецессии апсид. Он описывает эффекты добавления силы обратного куба к любой центральной силе. F(р), а не только к силам обратного квадрата, таким как Закон всемирного тяготения Ньютона и Закон Кулона. Теорема Ньютона упрощает орбитальные задачи в классическая механика исключив из рассмотрения силы обратного куба. Радиальные и угловые движения, р(т) и θ₁(т), можно вычислить без силы обратного куба; впоследствии его эффект можно рассчитать, умножив угловую скорость частицы

${\displaystyle \omega _{2}={\frac {d\theta _{2}}{dt}}=k{\frac {d\theta _{1}}{dt}}=k\omega _{1}.}$

Математическое утверждение

Воспроизвести медиа

Рисунок 4: Все три планеты совершают одинаковое радиальное движение (голубой круг), но движутся с разными угловыми скоростями. Голубая планета чувствует только обратный квадрат сила и движется по эллипс (k = 1). Зеленая планета движется под углом в три раза быстрее, чем голубая планета (k = 3); он совершает три витка для каждой орбиты голубой планеты. Красная планета иллюстрирует чисто радиальное движение без углового движения (k = 0). Пути, по которым следуют зеленые и синие планеты, показаны на Рисунок 9. А Гифка версия этой анимации найдена здесь.

Воспроизвести медиа

Рисунок 5: Зеленая планета движется под углом на одну треть быстрее, чем голубая планета (k = 1/3); он совершает один оборот на каждые три синих орбиты. Пути, по которым следуют зеленые и синие планеты, показаны на Рисунок 10. А Гифка версия этой анимации найдена здесь.

Рассмотрим частицу, движущуюся под произвольным центральная сила F₁(р), величина которого зависит только от расстояния р между частицей и неподвижным центром. Поскольку движение частицы под действием центральной силы всегда лежит в плоскости, положение частицы можно описать следующим образом: полярные координаты (р, θ₁), радиус и угол частицы относительно центра силы (Рисунок 1). Обе эти координаты, р(т) и θ₁(т), меняются со временем т как частица движется.

Представьте себе вторую частицу той же массы м и с таким же радиальным движением р(т), но с угловой скоростью k раз быстрее, чем у первой частицы. Другими словами, азимутальные углы двух частиц связаны уравнением θ₂(т) = k θ₁(т). Ньютон показал, что движение второй частицы может быть произведено добавлением центральной силы обратного куба к любой силе. F₁(р) действует на первую частицу^[19]

${\displaystyle F_{2}(r)-F_{1}(r)={\frac {L_{1}^{2}}{mr^{3}}}\left(1-k^{2}\right)}$

куда L₁ величина первой частицы угловой момент, который является постоянная движения (сохранено) для центральных сил.

Если k² больше единицы, F₂ − F₁ отрицательное число; таким образом, добавленная сила обратного куба равна привлекательный, как это наблюдается на зеленой планете на рисунках 1–4 и 9. Напротив, если k² меньше единицы, F₂−F₁ положительное число; добавленная сила обратного куба равна отталкивающий, как это наблюдается на зеленой планете на рисунках 5 и 10 и на красной планете на рисунках 4 и 5.

Изменение пути частицы

Добавление такой силы обратного куба также изменяет дорожка за которой следует частица. Траектория частицы игнорирует временные зависимости радиального и углового движений, такие как р(т) и θ₁(т); скорее, он связывает переменные радиуса и угла друг с другом. Для этой цели угловая переменная не ограничена и может неограниченно увеличиваться, поскольку частица несколько раз обращается вокруг центральной точки. Например, если частица дважды оборачивается вокруг центральной точки и возвращается в исходное положение, ее конечный угол не совпадает с ее начальным углом; скорее, он увеличился на 2×360° = 720°. Формально угловая переменная определяется как интеграл от угловой скорости

${\displaystyle \theta _{1}\equiv \int \omega _{1}(t)\,dt.}$

Аналогичное определение справедливо для θ₂, угол второй частицы.

Если путь первой частицы описан в виде р = грамм(θ₁), путь второй частицы задается функцией р = грамм(θ₂/k), поскольку θ₂ = k θ₁. Например, пусть путь первой частицы будет эллипс

${\displaystyle {\frac {1}{r}}=A+B\cos \theta _{1}}$

куда А и B константы; тогда путь второй частицы определяется выражением

${\displaystyle {\frac {1}{r}}=A+B\cos \left({\frac {\theta _{2}}{k}}\right).}$

Орбитальная прецессия

Если k близка, но не равна одной, вторая орбита похожа на первую, но постепенно вращается вокруг центра силы; это известно как орбитальная прецессия (Рисунок 3). Если k больше единицы, орбита прецессирует в том же направлении, что и орбита (рис. 3); если k меньше единицы, орбита прецессирует в обратном направлении.

Хотя может показаться, что орбита на рисунке 3 вращается равномерно, то есть с постоянной угловой скоростью, это верно только для круговых орбит.^[2][3] Если орбита вращается с угловой скоростью Ω, угловая скорость второй частицы больше или меньше угловой скорости первой частицы на Ω; другими словами, угловые скорости удовлетворяли бы уравнению ω₂ = ω₁ + Ом. Однако теорема Ньютона о вращающихся орбитах утверждает, что угловые скорости связаны умножением: ω₂ = kω₁, куда k является константой. Объединение этих двух уравнений показывает, что угловая скорость прецессии равна Ω = (k − 1)ω₁. Следовательно, Ω постоянно, только если ω₁ постоянно. Согласно сохранению углового момента, ω₁ изменяется с радиусом р

${\displaystyle \omega _{1}={\frac {L_{1}}{mr^{2}}};}$

куда м и L₁ первые частицы масса и угловой момент соответственно, оба из которых постоянны. Следовательно, ω₁ постоянно, только если радиус р постоянна, т.е. когда орбита представляет собой круг. Однако в этом случае орбита не изменяется при прецессии.

Наглядный пример: спирали Котеса

Рисунок 6: Для голубой частицы, движущейся по прямой линии, радиус р от данного центра изменяется с углом в соответствии с уравнением б = р cos (θ - θ₀), куда б расстояние наибольшего сближения (прицельный параметр, показаны красным).

Простейшая иллюстрация теоремы Ньютона возникает, когда нет начальной силы, т.е. F₁(р) = 0. В этом случае первая частица неподвижна или движется по прямой. Если он движется по прямой линии, которая не проходит через начало координат (желтая линия на рисунке 6), уравнение для такой линии может быть записано в полярных координатах (р, θ₁) в качестве

${\displaystyle {\frac {1}{r}}={\frac {1}{b}}\cos \ (\theta _{1}-\theta _{0})}$

куда θ₀ - угол, при котором расстояние минимизируется (рисунок 6). Расстояние р начинается с бесконечности (когда θ₁ – θ₀ = −90°), и постепенно уменьшается до тех пор, пока θ₁ – θ₀ = 0°, когда расстояние достигает минимума, то постепенно снова увеличивается до бесконечности при θ₁ – θ₀ = 90°. Минимальное расстояние б это прицельный параметр, которая определяется как длина перпендикуляра от фиксированного центра до линии движения. Такое же радиальное движение возможно, когда добавляется центральная сила, обратная кубу.

Рисунок 7: Эписпирали, соответствующие k равно 2/3 (красный), 1,0 (черный), 1,5 (зеленый), 3,0 (голубой) и 6,0 (синий). Когда k меньше единицы, сила обратного куба является отталкивающей, тогда как когда k больше единицы, сила притяжения.

Центральная сила обратного куба F₂(р) имеет вид

${\displaystyle F_{2}(r)={\frac {\mu }{r^{3}}}}$

где числитель μ может быть положительным (отталкивающим) или отрицательным (притягивающим). Если ввести такую ​​силу обратного куба, теорема Ньютона говорит, что соответствующие решения имеют форму, называемую Спирали Котеса^{[требуется разъяснение ]}. Это кривые, определяемые уравнением^[20][21]

${\displaystyle {\frac {1}{r}}={\frac {1}{b}}\cos \ \left({\frac {\theta _{2}-\theta _{0}}{k}}\right)}$

где постоянная k равно

${\displaystyle k^{2}=1-{\frac {m\mu }{L_{1}^{2}}}}$

Когда правая часть уравнения является положительной настоящий номер, решение соответствует эпспиральный.^[22] Когда аргумент θ₁ – θ₀ равно ± 90 ° ×k, косинус стремится к нулю, а радиус стремится к бесконечности. Таким образом, когда k меньше единицы, диапазон допустимых углов становится небольшим, а сила отталкивающая (красная кривая справа на рисунке 7). С другой стороны, когда k больше единицы, диапазон допустимых углов увеличивается, что соответствует силе притяжения (зеленая, голубая и синяя кривые слева на рисунке 7); орбита частицы может даже несколько раз огибать центр. Возможные значения параметра k может находиться в диапазоне от нуля до бесконечности, что соответствует значениям μ в диапазоне от отрицательной бесконечности до положительного верхнего предела, L₁²/м. Таким образом, для всех сил притяжения обратного куба (отрицательные μ) существует соответствующая эпспиральная орбита, как и для некоторых отталкивающих (μ < L₁²/м), как показано на рисунке 7. Более сильные силы отталкивания соответствуют более быстрому линейному движению.

Фигура 8: Спирали Пуансо (шиш спирали), соответствующие значениям λ, равным 1,0 (зеленый), 3,0 (голубой) и 6,0 (синий).

Один из других типов решений представлен в терминах гиперболический косинус:

${\displaystyle {\frac {1}{r}}={\frac {1}{b}}\cosh \ \left({\frac {\theta _{0}-\theta _{2}}{\lambda }}\right)}$

где постоянная λ удовлетворяет

${\displaystyle \lambda ^{2}={\frac {m\mu }{L_{1}^{2}}}-1}$

Эта форма спиралей Котеса соответствует одной из двух Спирали Пуансо (Рисунок 8).^[22] Возможные значения λ находятся в диапазоне от нуля до бесконечности, что соответствует значениям μ, превышающим положительное число. L₁²/м. Таким образом, спиральное движение Пуансо происходит только для отталкивающих центральных сил, обратных кубу, и применяется в том случае, если L не слишком велика для данного μ.

Принимая предел k или λ, стремящаяся к нулю, дает третью форму спирали Котеса, так называемую обратная спираль или же гиперболическая спираль, как решение^[23]

${\displaystyle {\frac {1}{r}}=A\theta _{2}+\varepsilon }$

куда А и ε - произвольные постоянные. Такие кривые возникают, когда сила отталкивания μ точно уравновешивает член угловой момент-масса

${\displaystyle \mu ={\frac {L_{1}^{2}}{m}}}$

Замкнутые орбиты и центральные силы обратного куба

Рисунок 9: Гармонические орбиты с k = 1 (синий), 2 (пурпурный) и 3 (зеленый). Анимация синей и зеленой орбит показана на рисунке 4.

Два типа центральные силы - линейно увеличивающиеся с расстоянием, F = Cr, Такие как Закон Гука, и силы обратного квадрата, F = C/р², Такие как Закон всемирного тяготения Ньютона и Закон Кулона - имеют очень необычное свойство. Частица, движущаяся под действием любого типа силы, всегда возвращается в исходное место со своей начальной скоростью, при условии, что ей не хватает энергии, чтобы уйти в бесконечность. Другими словами, путь связанной частицы всегда замкнут, и ее движение повторяется бесконечно, независимо от ее начального положения или скорости. Как показано Теорема Бертрана, это свойство неверно для других типов сил; в общем, частица не вернется в исходную точку с той же скоростью.

Однако теорема Ньютона показывает, что к частице, движущейся под действием линейной силы или силы обратного квадрата, может быть приложена обратная кубическая сила, так что ее орбита остается закрытым при условии, что k равно Рациональное число. (Число называется "рациональным", если его можно записать в виде дроби м/п, куда м и п являются целыми числами.) В таких случаях добавление обратно-кубической силы заставляет частицу завершить м вращение вокруг центра силы за то же время, что и исходная частица. п вращения. Этот метод создания замкнутых орбит не нарушает теорему Бертрана, поскольку добавленная обратно-кубическая сила зависит от начальной скорости частицы.

Рисунок 10: Субгармонические орбиты с k = 1 (синий), 1/2 (пурпурный) и 1/3 (зеленый). Анимация синей и зеленой орбит показана на рисунке 5.

Гармонические и субгармонические орбиты - особые типы таких замкнутых орбит. Замкнутая траектория называется гармоническая орбита если k является целым числом, т.е. если п = 1 в формуле k = м/п. Например, если k = 3 (зеленая планета на рисунках 1 и 4, зеленая орбита на рисунке 9), результирующая орбита является третьей гармоникой исходной орбиты. Наоборот, замкнутая траектория называется субгармоническая орбита если k это обратный целого числа, т.е. если м = 1 в формуле k = м/п. Например, если k = 1/3 (зеленая планета на рисунке 5, зеленая орбита на рисунке 10), получившаяся орбита называется третьей субгармоникой исходной орбиты. Хотя такие орбиты маловероятны в природе, они полезны для иллюстрации теоремы Ньютона.^[2]

Предел почти круговых орбит

В предложении 45 его PrincipiaНьютон применяет свою теорему о вращающихся орбитах для разработки метода нахождения силовых законов, управляющих движением планет.^[24] Иоганн Кеплер отметил, что орбиты большинства планет и Луны казались эллипсами, и длинная ось этих эллипсов может быть точно определена из астрономических измерений. Длинная ось определяется как линия, соединяющая позиции минимального и максимального расстояний до центральной точки, то есть линия, соединяющая две точки. апсиды. Для иллюстрации длинная ось планеты Меркурий определяется как линия, проходящая через ее последовательные положения перигелия и афелия. Со временем длинная ось большинства вращающихся тел постепенно поворачивается, обычно не более чем на несколько градусов за полный оборот, из-за гравитационных возмущений от других тел. сжатие в притягивающем теле, общие релятивистские эффекты, и другие эффекты. Метод Ньютона использует эту апсидальную прецессию в качестве чувствительного датчика типа силы, применяемой к планетам.^[25]

Теорема Ньютона описывает только эффекты добавления центральной силы обратного куба. Однако Ньютон распространяет свою теорему на произвольную центральную силу. F(р), ограничивая свое внимание почти круглыми орбитами, такими как эллипсы с низкой орбитальный эксцентриситет (ε ≤ 0,1), что верно для семи из восьми планетных орбит в Солнечная система. Ньютон также применил свою теорему к планете Меркурий,^[26] который имеет эксцентриситет ε примерно 0,21, и предположил, что это может относиться к Комета Галлея, чья орбита имеет эксцентриситет примерно 0,97.^[25]

Качественное обоснование этой экстраполяции его метода было предложено Валлури, Уилсоном и Харпером.^[25] Согласно их аргументам, Ньютон считал апсидальный угол прецессии α (угол между векторами последовательного минимального и максимального расстояния от центра) как гладкий, непрерывная функция эксцентриситета орбиты ε. Для силы, обратно пропорциональной квадрату, α равно 180 °; векторы к положениям минимального и максимального расстояний лежат на одной прямой. Если изначально α не равен 180 ° при малых ε (квазикруговые орбиты), то, как правило, α будет равняться 180 ° только для отдельных значений ε; случайно выбранное значение ε вряд ли даст α = 180 °. Таким образом, наблюдаемое медленное вращение апсид планетных орбит предполагает, что сила тяжести является законом обратных квадратов.

Количественная формула

Чтобы упростить уравнения, Ньютон пишет F(р) в терминах новой функции C(р)

${\displaystyle F(r)={\frac {C(r)}{Rr^{3}}}}$

куда р - средний радиус почти круговой орбиты. Ньютон расширяется C(р) в серии, теперь известной как Расширение Тейлора -в полномочия расстояния р, одно из первых появлений такого сериала.^[27] Приравнивая результирующий член силы обратного куба к силе обратного куба для вращающихся орбит, Ньютон выводит эквивалентный угловой коэффициент масштабирования k для почти круговых орбит ：^[24]

${\displaystyle {\frac {1}{k^{2}}}=\left({\frac {R}{C}}\right)\left.{\frac {dC}{dr}}\right|_{r=R}}$

Другими словами, приложение произвольной центральной силы F(р) на почти круговую эллиптическую орбиту может ускорить угловое движение в раз k без значительного влияния на радиальное движение. Если эллиптическая орбита неподвижна, частица вращается вокруг центра силы на 180 °, перемещаясь от одного конца длинной оси к другому (два апсиды ). Таким образом, соответствующий апсидальный угол α для общей центральной силы равна k× 180 °, используя общий закон θ₂ = k θ₁.

Примеры

Ньютон иллюстрирует свою формулу тремя примерами.В первых двух центральная сила - это сила закона, F(р) = р^п−3, так C(р) пропорциональна р^п. Приведенная выше формула показывает, что угловое движение умножается на коэффициент k = 1/√п, так что апсидальный угол α равно 180 ° /√п.

Этот угловой масштаб можно увидеть в апсидальной прецессии, то есть в постепенном вращении длинной оси эллипса (рис. 3). Как отмечалось выше, орбита в целом вращается со средней угловой скоростью Ω=(k−1)ω, куда ω равна средней угловой скорости частицы относительно стационарного эллипса. Если частица требует времени Т для перехода от одной апсиды к другой это означает, что при этом длинная ось будет вращаться на угол β = ΩТ = (k − 1)ωT = (k - 1) × 180 °. Для закон обратных квадратов Такие как Закон всемирного тяготения Ньютона, куда п равно 1, углового масштабирования нет (k = 1) апсидальный угол α равна 180 °, а эллиптическая орбита стационарна (Ω =β = 0).

В качестве последней иллюстрации Ньютон рассматривает сумму двух степенных законов

${\displaystyle C(r)\propto ar^{m}+br^{n}}$

который умножает угловую скорость на коэффициент

${\displaystyle k={\sqrt {\frac {a+b}{am+bn}}}}$

Ньютон применяет обе эти формулы (степенной закон и сумму двух степенных законов) для изучения апсидальной прецессии орбиты Луны.

Прецессия орбиты Луны

Движение Луны более сложное, чем у планет, в основном из-за конкурирующего гравитационного притяжения Земли и Солнца.

Движение Луна можно точно измерить, и он заметно сложнее, чем у планет.^[28] Древнегреческие астрономы, Гиппарх и Птолемей, отметил несколько периодических изменений орбиты Луны,^[28] такие как небольшие колебания в его орбитальный эксцентриситет и склонность его орбиты к плоскости эклиптика. Эти колебания обычно происходят раз в месяц или два раза в месяц. Линия его апсиды прецессирует постепенно с периодом примерно 8,85 года, в то время как его линия узлов делает полный круг примерно вдвое больше, чем за 18,6 года.^[29] Это объясняет примерно 18-летнюю периодичность затмения, так называемой Цикл Сароса. Однако обе линии испытывают небольшие колебания в своем движении, опять же в месячном масштабе.

В 1673 г. Джеремайя Хоррокс опубликовал достаточно точную модель движения Луны, в которой предполагалось, что Луна следует по прецессирующей эллиптической орбите.^[30][31] Достаточно точный и простой метод предсказания движения Луны решил бы навигационную задачу определения движения корабля. долгота;^[32] во времена Ньютона целью было предсказать положение Луны с точностью до 2 '(два угловые минуты ), что соответствовало бы ошибке земной долготы в 1 °.^[33] Модель Хоррокса предсказывала положение Луны с ошибкой не более 10 угловых минут;^[33] для сравнения, диаметр Луны составляет примерно 30 угловых минут.

Ньютон использовал свою теорему о вращающихся орбитах двумя способами для объяснения апсидальной прецессии Луны.^[34] Во-первых, он показал, что наблюдаемую апсидальную прецессию Луны можно объяснить изменением силовой закон гравитации от закона обратных квадратов к сила закона в котором показатель был 2 + 4/243 (примерно 2,0165)^[35]

${\displaystyle F(r)=-{\frac {GMm}{r^{2+4/243}}}}$

В 1894 г. Асаф Холл принял этот подход, слегка изменив показатель степени в законе обратных квадратов, чтобы объяснить аномальный орбитальный прецессия из планета Меркурий,^[36] который наблюдал в 1859 г. Урбен Леверье.^[37] По иронии судьбы теория Холла была опровергнута тщательными астрономическими наблюдениями Луны.^[38] В принятое в настоящее время объяснение поскольку эта прецессия включает в себя теорию общая теория относительности, который (к первое приближение ) добавляет силу обратной четвертичной степени, то есть силу, которая изменяется как обратная четвертая степень расстояния.^[39]

В качестве второго подхода к объяснению прецессии Луны Ньютон предположил, что возмущающее влияние солнце на движение Луны может быть приблизительно эквивалентно дополнительной линейной силе

${\displaystyle F(r)={\frac {A}{r^{2}}}+Br}$

Первый член соответствует гравитационному притяжению между Луной и Землей, где р расстояние Луны от Земли. Второй член, как рассуждал Ньютон, может представлять собой среднюю возмущающую силу гравитации Солнца в системе Земля-Луна. Такой закон силы мог бы также возникнуть, если бы Земля была окружена сферическим пылевым облаком однородной плотности.^[40] Используя формулу для k для почти круговых орбит и оценки А и B, Ньютон показал, что этот силовой закон не может объяснить прецессию Луны, поскольку предсказанный апсидный угол α составляла (≈ 180,76 °), а не наблюдаемая α (≈ 181,525 °). За каждый оборот длинная ось поворачивается на 1,5 °, примерно половину наблюдаемых 3,0 °.^[34]

Обобщение

Исаак Ньютон впервые опубликовал свою теорему в 1687 году в качестве предложений 43–45 книги I его Philosophiæ Naturalis Principia Mathematica. Однако как астрофизик Субраманян Чандрасекар отметил в своем комментарии 1995 г. PrincipiaТеорема оставалась в значительной степени неизвестной и неразработанной более трех столетий.^[1]

Первое обобщение теоремы Ньютона было открыто Магомедом и Вавда в 2000 году.^[4] Как и Ньютон, они предположили, что угловое движение второй частицы k раз быстрее, чем у первой частицы, θ₂ = k θ₁. Однако, в отличие от Ньютона, Магомед и Вауда не требовали, чтобы радиальное движение двух частиц было одинаковым, р₁ = р₂. Скорее, они требовали, чтобы обратные радиусы были связаны линейным уравнением

${\displaystyle {\frac {1}{r_{2}(t)}}={\frac {a}{r_{1}(t)}}+b}$

Это преобразование переменных изменяет путь частицы. Если путь первой частицы записан р₁ = грамм(θ₁), путь второй частицы можно записать как

${\displaystyle {\frac {ar_{2}}{1-br_{2}}}=g\left({\frac {\theta _{2}}{k}}\right)}$

Если движение первой частицы вызывается центральной силой F₁(р), Магомед и Вауда показали, что движение второй частицы может быть вызвано следующей силой

${\displaystyle F_{2}(r_{2})={\frac {a^{3}}{\left(1-br_{2}\right)^{2}}}F_{1}\left({\frac {ar_{2}}{1-br_{2}}}\right)+{\frac {L^{2}}{mr^{3}}}\left(1-k^{2}\right)-{\frac {bL^{2}}{mr^{2}}}}$

Согласно этому уравнению вторая сила F₂(р) получается путем масштабирования первой силы и изменения ее аргумента, а также путем добавления центральных сил обратного квадрата и обратного куба.

Для сравнения: теорема Ньютона о вращающихся орбитах соответствует случаю а = 1 и б = 0, так что р₁ = р₂. В этом случае исходная сила не масштабируется, и ее аргумент не изменяется; сила обратного куба добавляется, а член обратного квадрата - нет. Кроме того, путь второй частицы равен р₂ = грамм(θ₂/k)в соответствии с приведенной выше формулой.

Производные

Вывод Ньютона

Вывод Ньютона находится в разделе IX его Principia, а именно предложения 43–45.^[41] Его выводы этих предложений основаны в основном на геометрии.

Предложение 43; Проблема 30

Диаграмма, иллюстрирующая вывод Ньютона. Голубая планета движется по пунктирной эллиптической орбите, а зеленая планета движется по сплошной эллиптической орбите; два эллипса имеют общие фокус в момент C. Углы UCP и VCQ равны θ₁, а черная дуга представляет угол UCQ, который равен θ₂ = k θ₁. Сплошной эллипс повернулся относительно пунктирного эллипса на угол UCV, равный (k−1) θ₁. Все три планеты (красная, синяя и зеленая) находятся на одинаковом расстоянии р из центра силы C.

Требуется заставить тело двигаться по кривой, которая вращается вокруг центра силы так же, как другое тело по той же кривой в состоянии покоя.^[42]

Вывод предложения 43 Ньютоном зависит от его предложения 2, полученного ранее в Principia.^[43] Предложение 2 обеспечивает геометрическую проверку того, является ли результирующая сила, действующая на точечную массу (частицу) центральная сила. Ньютон показал, что сила является центральной тогда и только тогда, когда частица выметает равные площади за равное время, измеренное от центра.

Вывод Ньютона начинается с частицы, движущейся под произвольной центральной силой. F₁(р); движение этой частицы под действием этой силы описывается ее радиусом р(т) от центра как функция времени, а также его угол θ₁(т). В бесконечно малое время dt, частица выметает приближенный прямоугольный треугольник, площадь которого равна

${\displaystyle dA_{1}={\frac {1}{2}}r^{2}d\theta _{1}}$

Поскольку сила, действующая на частицу, считается центральной силой, частица выметает равные углы за равное время в соответствии с предложением Ньютона 2. Иначе говоря, ставка площади подметания постоянна

${\displaystyle {\frac {dA_{1}}{dt}}={\frac {1}{2}}r^{2}{\frac {d\theta _{1}}{dt}}=\mathrm {constant} }$

Эта постоянная площадная скорость можно рассчитать следующим образом. На апапсис и периапсис, позиции ближайшего и самого дальнего расстояния от центра притяжения, вектора скорости и радиус перпендикулярны; Следовательно угловой момент L₁ на массу м частицы (записывается как час₁) может быть связано со скоростью выметания участков

${\displaystyle h_{1}={\frac {L_{1}}{m}}=rv_{1}=r^{2}{\frac {d\theta _{1}}{dt}}=2{\frac {dA_{1}}{dt}}}$

Теперь рассмотрим вторую частицу, орбита которой идентична по радиусу, но угловое изменение которой умножено на постоянный коэффициент. k

${\displaystyle \theta _{2}(t)=k\theta _{1}(t)\,\!}$

Поверхностная скорость второй частицы равна скорости первой частицы, умноженной на тот же коэффициент. k

${\displaystyle h_{2}=2{\frac {dA_{2}}{dt}}=r^{2}{\frac {d\theta _{2}}{dt}}=kr^{2}{\frac {d\theta _{1}}{dt}}=2k{\frac {dA_{1}}{dt}}=kh_{1}}$

С k - постоянная величина, вторая частица также заметает равные площади за равное время. Следовательно, согласно предложению 2, на вторую частицу также действует центральная сила F₂(р). Это заключение предложения 43.

Предложение 44.

Разница сил, с помощью которых два тела могут двигаться одинаково, одно по фиксированной, а другое по одной и той же вращающейся орбите, изменяется обратно пропорционально кубу их общих высот.^[44]

Чтобы узнать величину F₂(р) от исходной центральной силы F₁(р), Ньютон вычислил их разность F₂(р) − F₁(р) используя геометрию и определение центростремительное ускорение. В предложении 44 его Principia, он показал, что разница пропорциональна кубу, обратному радиусу, в частности, по приведенной выше формуле, которую Ньютон записывает через две постоянные поверхностные скорости: час₁ и час₂

${\displaystyle F_{2}(r)-F_{1}(r)=m{\frac {h_{1}^{2}-h_{2}^{2}}{r^{3}}}}$

Предложение 45; Проблема 31

Найти движение апсид на орбитах, очень близких к окружностям.^[24]

В этом предложении Ньютон выводит следствия своей теоремы о вращающихся орбитах в пределе почти круговых орбит. Это приближение обычно справедливо для планетных орбит и орбиты Луны вокруг Земли. Это приближение также позволяет Ньютону рассматривать большое количество законов центральной силы, а не только законы обратных квадратов и обратных кубов.

Современное происхождение

Современные выводы теоремы Ньютона опубликованы Whittaker (1937)^[45] и Чандрасекхар (1995).^[42] По предположению вторая угловая скорость равна k раз быстрее, чем первый

${\displaystyle \omega _{2}={\frac {d\theta _{2}}{dt}}=k{\frac {d\theta _{1}}{dt}}=k\omega _{1}}$

Поскольку два радиуса ведут себя одинаково со временем, р(т) сохраняющиеся угловые моменты связаны тем же множителем k

${\displaystyle L_{2}=mr^{2}\omega _{2}=mr^{2}k\omega _{1}=kL_{1}\,\!}$

Уравнение движения для радиуса р частицы массы м переезд в центральный потенциал V(р) дан кем-то Уравнения Лагранжа

${\displaystyle m{\frac {d^{2}r}{dt^{2}}}-mr\omega ^{2}=m{\frac {d^{2}r}{dt^{2}}}-{\frac {L^{2}}{mr^{3}}}=F(r)}$

Применение общей формулы к двум орбитам приводит к уравнению

${\displaystyle m{\frac {d^{2}r}{dt^{2}}}=F_{1}(r)+{\frac {L_{1}^{2}}{mr^{3}}}=F_{2}(r)+{\frac {L_{2}^{2}}{mr^{3}}}=F_{2}(r)+{\frac {k^{2}L_{1}^{2}}{mr^{3}}}}$

который может быть преобразован в форму

${\displaystyle F_{2}(r)=F_{1}(r)+{\frac {L_{1}^{2}}{mr^{3}}}\left(1-k^{2}\right)}$

Это уравнение, связывающее две радиальные силы, можно качественно понять следующим образом. Разница угловых скоростей (или, что то же самое, угловых моментов) вызывает разницу в центростремительная сила требование; чтобы компенсировать это, радиальная сила должна быть изменена на силу, обратную кубу.

Теорема Ньютона может быть выражена эквивалентным образом через потенциальная энергия, который определен для центральных сил

${\displaystyle F(r)=-{\frac {dV}{dr}}}$

Уравнение радиальной силы можно записать в терминах двух потенциальная энергия

${\displaystyle -{\frac {dV_{2}}{dr}}=-{\frac {dV_{1}}{dr}}+{\frac {L_{1}^{2}}{mr^{3}}}\left(1-k^{2}\right)}$

Интегрируя по расстоянию р, Теорема Ньютона утверждает, что k-кратное изменение угловой скорости является результатом прибавления потенциальной энергии в обратном квадрате к любой заданной потенциальной энергии V₁(р)

${\displaystyle V_{2}(r)=V_{1}(r)+{\frac {L_{1}^{2}}{2mr^{2}}}\left(1-k^{2}\right)}$

Геометрическое доказательство Ньютона из принципов

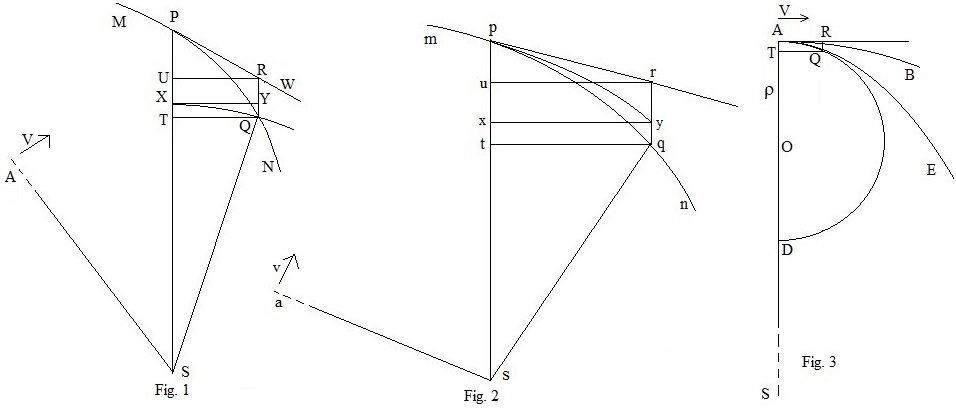
Упрощенное геометрическое доказательство предложения 44.

Хотя Ньютон утверждает, что проблема должна была быть решена с помощью предложения 6, он не использует его явно. В следующем упрощенном доказательстве предложение 6 используется, чтобы показать, как выводится результат.

Подробное доказательство Ньютона следует за этим, и, наконец, прилагается предложение 6, поскольку оно малоизвестно.

Предложение 44 использует предложение 6 для доказательства результата о вращающихся орбитах. В предложениях, следующих за предложением 6 раздела 2 Принципов, он применяет его к конкретным кривым, например к коническим сечениям. В случае предложения 44 оно применяется к любой орбите под действием произвольной силы, направленной к фиксированной точке, чтобы создать соответствующую вращающуюся орбиту.

На рис. 1 MN является частью этой орбиты. В точке P тело движется к Q под действием силы, направленной к S, как и раньше. Сила F (SP) определяется в каждой точке P кривой.

На рис. 2 соответствующая часть вращающейся орбиты - это mn с s в качестве центра силы. Предположим, что первоначально тело на статической орбите стартует под прямым углом к ​​радиусу со скоростью V. Тело на вращающейся орбите также должно начинаться под прямым углом и предполагать, что его скорость равна v. В случае, показанном на рис.1, ${\displaystyle v>V}$ и сила направлена ​​к S. Аргумент одинаково применим, если${\displaystyle v<V}$. Также сила может быть направлена ​​от центра.

Пусть SA будет начальным направлением статической орбиты, а sa - направлением вращающейся орбиты. Если через некоторое время тела на соответствующих орбитах окажутся в точках P и p, то отношения углов ${\displaystyle {\frac {asp}{ASP}}={\frac {psq}{PSQ}}={\frac {v}{V}}}$; соотношения площадей${\displaystyle {\frac {asp}{ASP}}={\frac {psq}{PSQ}}={\frac {v}{V}}}$; и радиусы${\displaystyle SP=sp}$, ${\displaystyle SQ=sq}$, ${\displaystyle SA=sa}$.

Фигура pryx и дуга py на фиг. 2 - это фигура PRQT и дуга PQ на фиг. 1, растянутые линейно в горизонтальном направлении в соотношении ${\displaystyle {\frac {v}{V}}}$, так что${\displaystyle PU=pu}$,${\displaystyle UT=ux}$, и ${\displaystyle qt={\frac {v}{V}}QT}$. Прямые qt и QT действительно должны быть дугами окружности с центрами s и S и радиусами sq и SQ соответственно. В пределе их соотношение становится ${\displaystyle {\frac {v}{V}}}$, будь то прямые или дуги.

Поскольку в пределе силы параллельны SP и sp, если бы на тело на фиг. 2 действовала та же сила, что и на фиг. 1, то тело прибыло бы в точку y, поскольку ry = RQ. Разница в горизонтальной скорости не влияет на вертикальные расстояния. Ньютон ссылается на следствие 2 законов движения, в котором движение тел разделяется на составляющую в радиальном направлении, на которую действует вся сила, и на другую составляющую, поперечную к ней, на которую не действует никакая сила.

Однако расстояние от y до центра, s, теперь больше, чем SQ, поэтому для перемещения тела к q требуется дополнительная сила, так что sq = SQ. Дополнительная сила представлена ​​yq, а f пропорциональна ry + yq, так же как F пропорционально RQ.

${\displaystyle RQ=SP-PU-ST}$, ${\displaystyle rq=sp-pu-st=RQ+ST-st}$.

Разница, ${\displaystyle ST-st=yq}$, можно найти следующим образом:

${\displaystyle ST^{2}=SQ^{2}-QT^{2}}$,${\displaystyle st^{2}=sq^{2}-qt^{2}}$, так ${\displaystyle (ST-st)(ST+st)=qt^{2}-QT^{2}}$.

А в пределе, когда QT и qt стремятся к нулю,${\displaystyle ST+st}$ становится равным${\displaystyle SQ+sq}$ или 2SP так

${\displaystyle yq*2SP={\frac {QT^{2}(v^{2}-V^{2})}{V^{2}}}}$.

Следовательно,${\displaystyle rq=RQ+ST-st=RQ+{\frac {QT^{2}(v^{2}-V^{2})}{2SP*V^{2}}}}$.

Поскольку из предложения 6 (рис.1 и см. Ниже) сила равна${\displaystyle {\frac {k*QR}{(SP^{2}*QT^{2})}}}$.Поделить на ${\displaystyle {\frac {(SP^{2}*QT^{2})}{k}}}$, где k - постоянная величина, чтобы получить силы${\displaystyle f(sp)=F(sp)+{\frac {k(v^{2}-V^{2})}{2sp^{3}*V^{2}}}}$.

На рис. 3 в начальной точке A статической кривой проведите касательную AR, которая перпендикулярна SA, и окружность AQD, которая касается кривой в точке A. Пусть ρ - радиус этой окружности. Поскольку угол SAR является прямым углом, центр круга лежит на SA. Из свойства круга:${\displaystyle QT^{2}=AT(2\rho -AT)=RQ(2\rho -RQ)}$, а в пределе, когда Q приближается к A, это становится${\displaystyle \rho =QT^{2}/2RQ}$.

Следовательно,${\displaystyle F(SA)={\frac {k}{(2\rho *SA^{2})}}}$.

А поскольку F (SA) задана, это определяет постоянную k. Однако Ньютон хочет, чтобы сила в точке A имела вид${\displaystyle cV^{2}/SA^{2}}$, где c - постоянная, так что${\displaystyle f(sp)=F(sp)+{\frac {c\rho (v^{2}-V^{2})}{sp^{3}}}}$,куда${\displaystyle c={\frac {F(SA)*SA^{2}}{V^{2}}}}$.

Выражение для f (sp) выше такое же, как у Ньютона в следствии 4 предложения 44, за исключением того, что он использует другие буквы. Он написал ${\displaystyle {\frac {G}{F}}={\frac {v}{V}}}$ (где G и F не обязательно равны v и V соответственно) и использует букву «V» для константы, соответствующей «c», и букву «X» для функции F (sp).

Приведенное выше геометрическое доказательство очень ясно показывает, откуда возникает дополнительная сила, заставляющая орбиту вращаться по отношению к статической орбите.

Доказательство предложения 44 Ньютоном

Доказательство Ньютона сложно ввиду простоты приведенного выше доказательства. Например, его доказательство требует некоторой расшифровки, как показано в следующем предложении:

«И поэтому, если с центром C и любым радиусом CP или Cp описывается круговой сектор, равный общей площади VPC, которую тело P, вращающееся по неподвижной орбите, в любое время описывало радиусом, проведенным к центру, разница между силы, с помощью которых тело P на неподвижной орбите и тело p на подвижной орбите вращаются, будут равны центростремительной силе, с помощью которой какое-либо тело с радиусом, проведенным к центру, могло бы описать этот сектор однородно в том же самом время, когда область VPC описывалась как G² - F² к F².”

Первоначально он рассматривает бесконечно малые ${\displaystyle \tau }$ при фиксированном значении площади SPQ и spq пропорциональны V и v соответственно; следовательно,${\displaystyle QT*SP\propto V\tau }$ и ${\displaystyle qt*sp\propto v\tau }$ в каждой из точек P и p, и${\displaystyle yq={\frac {qt^{2}-QT^{2}}{2sp}}\propto {\frac {1}{sp^{3}}}}$ поэтому дополнительная сила изменяется обратно пропорционально кубу радиуса.

На рисунке 1 XQ представляет собой дугу окружности с центром S и радиусом SQ, пересекающую SP в точке X. Перпендикуляр XY пересекает RQ в точке Y и ${\displaystyle YQ={\frac {QT^{2}}{2SP}}}$.

Позволять ${\displaystyle \phi (SQ)}$ быть силой, необходимой для того, чтобы заставить тело двигаться по окружности радиуса SQ, если она имеет ту же скорость, что и поперечная скорость тела на статической орбите в Q.

${\displaystyle {\frac {f(sp)-F(sp)}{\phi (sp)}}={\frac {yq}{YQ}}={\frac {(qt^{2}-QT^{2})}{QT^{2}}}={\frac {(v^{2}-V^{2})}{V^{2}}}}$

в каждой точке P и, в частности, на верхней стороне A:

${\displaystyle {\frac {f(SA)-F(SA)}{\phi (SA)}}={\frac {(v^{2}-V^{2})}{V^{2}}}}$.

Но в точке A на рис. 3 отношение силы, заставляющей тело двигаться по статической кривой AE, к силе, необходимой для того, чтобы заставить его двигаться по окружности AB с радиусом SA, обратно пропорционально отношению их радиусов. кривизны, поскольку они оба движутся с одинаковой скоростью V перпендикулярно SA:${\displaystyle {\frac {F(SA)}{\phi (SA)}}={\frac {SA}{\rho }}}$.Из первой части доказательства ${\displaystyle f(sp)-F(sp)={\frac {(f(sa)-F(sa))sa^{3}}{sp^{3}}}={\frac {\rho F(sa)sa^{2}(v^{2}-V^{2})}{V^{2}sp^{3}}}}$.

Подставляя выражение Ньютона для F (SA), дает результат, полученный ранее.

Доказательство предложения 45 Ньютоном

«Чтобы найти движение апсидов по орбитам, приближающимся к кругам».

Предложение 44 было разработано специально для доказательства этого предложения.Ньютон хочет исследовать движение тела по почти круговой орбите, притягиваемого силой вида${\displaystyle f(sp)=\gamma *sp^{n-3}}$.

Он аппроксимирует статическую кривую эллипсом с силой, обратной квадрату, F (SP), направленной к одному из фокусов, заставленных вращаться добавлением силы, обратной кубу, согласно Предложению 44.

Для статического эллипса с силой, обратно пропорциональной квадрату SP,${\displaystyle F(SP)={\frac {cV^{2}}{SP^{2}}}}$, поскольку c определено выше, так что ${\displaystyle F(SA)={\frac {cV^{2}}{SA^{2}}}}$.

Когда тело находится на статической орбите, начиная с верхней апсайды в точке A, оно достигнет нижней апсайды, точки, ближайшей к S, после перемещения на угол 180 градусов. Ньютону нужна соответствующая вращающаяся орбита, начинающаяся от апсайды a, вокруг точки s, с нижней апсайдерской стороной, смещенной на угол, α, где ${\displaystyle {\frac {(180+\alpha )}{180}}={\frac {v}{V}}}$.

Начальная скорость V в точке A должна быть чуть меньше, чем требуется, чтобы тело двигалось по кругу. Тогда ρ можно принять равным SA или sa. Проблема состоит в том, чтобы определить v по значению n, чтобы можно было найти α или задать α, чтобы найти n.

${\displaystyle f(sp)=F(sp)+{\frac {c\rho (v^{2}-V^{2})}{sp^{3}}}={\frac {c(sp*V^{2}+sa(v^{2}-V^{2}))}{sp^{3}}}}$

Сдача ${\displaystyle sp=sa-X}$,

${\displaystyle f(sp)={\frac {c(s*av^{2}-XV^{2})}{sp^{3}}}}$.

Затем «нашим методом сходящихся рядов»:${\displaystyle f(sp)={\frac {\gamma *sp^{n}}{sp^{3}}}={\frac {\gamma (sa-X)^{n}}{sp^{3}}}={\frac {\gamma *sa^{n-1}(sa-nX)}{sp^{3}}}}$ плюс термины в X² и выше, которые можно игнорировать, потому что орбита почти круглая, поэтому X мало по сравнению с sa.

Сравнивая 2 выражения для f (sp), ${\displaystyle f(sp)={\frac {\gamma *sa^{n-1}(sa-nX)}{sp^{3}}}={\frac {c(sa*v^{2}-XV^{2})}{sp^{3}}}}$следует, что${\displaystyle {\frac {v}{V}}={\frac {1}{n^{1/2}}}={\frac {(180+\alpha )}{180}}}$.

Также, ${\displaystyle f(sp)={\frac {cv^{2}*sp^{n-3}}{sa^{n-1}}}}$.

Отношение начальных сил при a определяется выражением${\displaystyle {\frac {f(sa)}{F(sa)}}={\frac {1}{n}}}$.

Предложение 6 для доказательства предложения 44 выше.

На рис.1 тело движется по определенной кривой MN, на которую действует (центростремительная) сила, к фиксированной точке S. Сила зависит только от расстояния точки от S. Цель этого предложения состоит в том, чтобы определить как сила изменяется с радиусом, SP. Метод в равной степени применим к случаю, когда сила центробежная.

За короткое время ${\displaystyle \tau }$, тело перемещается из P в ближайшую точку Q. Нарисуйте QR параллельно SP, пересекая касательную в точке R, и QT перпендикулярно SP, пересекаясь с ней в точке T.

Если бы не было силы, он двигался бы по касательной в точке P со скоростью, которую он имел в точке P, достигая точки R. Если бы сила, действующая на тело, движущееся из точки P в точку Q, была постоянной по величине и параллельной направлению в направлении SP дуга PQ будет параболической с PR в качестве касательной, а QR будет пропорционален этой постоянной силе и квадрату времени, ${\displaystyle \tau }$.

И наоборот, если вместо того, чтобы достичь R, тело отклонилось на Q, то постоянная сила, параллельная SP, с величиной:${\displaystyle F\propto {\frac {QR}{\tau ^{2}}}}$ заставил бы его достичь Q вместо R.

Однако, поскольку направление радиуса от S к точкам на дуге PQ, а также величина силы по направлению к S будут изменяться вдоль PQ, указанное выше соотношение не даст точной силы в P. Если Q достаточно близко к P, направление силы будет почти параллельно SP на всем протяжении PQ, и, если сила изменится незначительно, можно предположить, что PQ аппроксимируется параболической дугой с силой, указанной выше в терминах QR и ${\displaystyle \tau }$.

Время, ${\displaystyle \tau }$ пропорциональна площади сектора SPQ. Это второй закон Кеплера. Доказательство представлено в предложении 1 книги 1 Принципов. Поскольку дугу PQ можно аппроксимировать прямой линией, площадь сектора SPQ и площадь треугольника SPQ можно принять равными, поэтому

${\displaystyle F\propto {\frac {QR}{\tau ^{2}}}={\frac {k*QR}{(SP^{2}*QT^{2})}}}$, где k - постоянная величина.

Опять же, это не точно для конечных длин PQ. Закон силы получается, если предел приведенного выше выражения существует как функция SP, когда PQ приближается к нулю.

Фактически, со временем ${\displaystyle \tau }$, тело без силы достигло бы точки W дальше от P, чем R. Однако в пределе QW становится параллельным SP. Точка W в доказательстве Ньютона игнорируется.

Кроме того, Ньютон описывает QR как проверенный синус дуги с P в центре и длиной вдвое QP. Хотя это не совсем то же самое, что QR, который он имеет на диаграмме (рис.1), в пределе они становятся равными.

Примечания:

Это предложение основано на анализе Галилеем тела, движущегося по параболической траектории под действием постоянного ускорения. В предложении 10 он описывает это как теорему Галилея и несколько раз упоминает Галилея в связи с ней в «Началах». Объединение его со вторым законом Кеплера дает простой и элегантный метод.

В исторически очень важном случае, когда MN на рис.1 был частью эллипса, а S - одним из его фокусов, Ньютон показал в предложении 11, что предел ${\displaystyle QR/QT^{2}}$ была постоянной в каждой точке кривой, так что сила, действующая на тело, направленная к фиксированной точке S, изменялась обратно пропорционально квадрату расстояния SP.

Помимо эллипса с центром в фокусе, Ньютон также применил предложение 6 к гиперболе (предложение 12), параболе (предложение 13), эллипсу с центром силы в центре эллипса (предложение 10), равноугольной спираль (Предложение 9), а также окружность с центром силы, не совпадающим с центром, и даже на окружности (Предложение 7).

Смотрите также

• Проблема Кеплера
• Вектор Лапласа – Рунге – Ленца.
• Теорема Бертрана
• Задача двух тел в общей теории относительности
• Теорема Ньютона об овалах

Рекомендации

1. Чандрасекхар, стр. 183.
2. Линден-Белл, Д; Линден-Белл Р.М. (1997). «О формах вращающихся орбит Ньютона». Примечания и отчеты Лондонского королевского общества. 51 (2): 195–198. Дои:10.1098 / рснр.1997.0016. S2CID  73239002.
3. Линден-Белл Д., Джин С. (2008). «Аналитические центральные орбиты и их группа преобразований». Ежемесячные уведомления Королевского астрономического общества. 386 (1): 245–260. arXiv:0711.3491. Bibcode:2008МНРАС.386..245Л. Дои:10.1111 / j.1365-2966.2008.13018.x. S2CID  15451037.
4. Магомед FM, Vawda F (2000). «Применение симметрий к задачам центральной силы». Нелинейная динамика. 21 (4): 307–315. Дои:10.1023 / А: 1008317327402. S2CID  116319304.
5. Немирофф, Роберт (13 июня 2010 г.). «Ретроградный Марс». Астрономическая картина дня. НАСА. В архиве из оригинала 31 мая 2011 г.. Получено 31 октября 2016.
6. Sugon QM, Bragais S, McNamara DJ (2008) Эпициклы Коперника из закона гравитационной силы Ньютона через линейную теорию возмущений в геометрической алгебре В архиве 2016-10-29 на Wayback Machine.
7. Хейльброн 2005, стр.11
8. Фитцпартрик 2012, стр. 41–43
9. Ламбурн 2010, стр. 204–205
10. Уиттакер, стр. 339–385.
11. Сундман К.Ф. (1912). "Memoire sur le проблема де труа корпус". Acta Mathematica. 36 (1): 105–179. Дои:10.1007 / BF02422379.
12. Хильтебайтель А.М. (1911). «К проблеме двух неподвижных центров и некоторых ее обобщениях». Американский журнал математики. Издательство Университета Джона Хопкинса. 33 (1/4): 337–362. Дои:10.2307/2369997. JSTOR  2369997.
13. Хейльброн 2005, стр.139
14. Коэн, стр. 147.
15. Clairaut, AC (1745). "Du Système du Monde dans les Principes de la Gravitation Universelle". Histoire de l'Académie Royale des Sciences avec les mathématique et de Physique. 1749: 329–364. В архиве из оригинала 2011-06-07. Получено 2007-07-12.
16. Hill GW (1894 г.). «Буквальное выражение движения перигея Луны». Анна. Математика. 9 (1/6): 31–41. Дои:10.2307/1967502. JSTOR  1967502.
17. Браун EW (1891). «Неизвестный титул». Являюсь. J. Math. Издательство Университета Джона Хопкинса. 13 (2): 159–172. Дои:10.2307/2369812. JSTOR  2369812.
    Браун EW (1891). «Об определении определенного класса неравенств в движении Луны». Ежемесячные уведомления Королевского астрономического общества. 52 (2): 71. Bibcode:1891МНРАС..52 ... 71Б. Дои:10.1093 / mnras / 52.2.71.
18. Делоне С (1862 г.). «Неизвестный титул». Mémoires Acad. Imp. Sc.: 237.
    Делоне С (1867 г.). «Неизвестный титул». Mémoires Acad. Imp. Sc.: 451.
19. Ньютон, Principia, раздел IX книги I, предложения 43–45, стр. 135–147.
20. Гроссман 1996, стр. 33–34
21. Шикин 1995, стр. 139–140
22. Лоуренс 1972, стр. 192–194
23. Вайсштейн 2002, стр. 1427
24. Чандрасекхар С 1995, стр. 192–194
25. Валлури С. Р .; Wilson C .; Харпер В. (1997). "Апсидальная теорема Ньютона о прецессии и эксцентрические орбиты". Журнал истории астрономии. 28: 13–27. Bibcode:1997JHA .... 28 ... 13В. Дои:10.1177/002182869702800102. S2CID  117886193.
26. Ньютон, Principia, Книга III, Предложение 2, с. 406.
27. Коэн И.Б. (1990). "Два эссе Галлея о Ньютоне" Principia". В Нормане Троуэре (ред.). Стоя на плечах гигантов: более длинный взгляд на Ньютона и Галлея. Беркли, Калифорния: Калифорнийский университет Press. стр.91–108. ISBN  978-0-520-06589-5.
28. Повар А (2000). «Успех и неудача в лунной теории Ньютона». Астрономия и геофизика. 41 (6): 21–25. Bibcode:2000A и G .... 41f..21C. Дои:10.1046 / j.1468-4004.2000.41621.x.
29. Смит, стр. 252.
30. Хоррокс Дж. (1673). Иеремия Гороци, опера posthuma. Лондон: G Godbit для Дж. Мартина.
31. Уилсон C (1987). «О происхождении лунной теории Хоррока». Журнал истории астрономии. 18 (2): 77–94. Bibcode:1987JHA .... 18 ... 77 Вт. Дои:10.1177/002182868701800201. S2CID  115379870.
32. Коллерстрем Н (2000). Забытая лунная теория Ньютона: его вклад в поиски долготы. Green Lion Press. ISBN  978-1-888009-08-8.
33. Смит, стр. 254.
34. Ньютон, Principia, Книга I, раздел IX, предложение 45, стр. 141–147.
35. Чандрасекхар, стр. 198.
36. Зал А (1894 г.). «Предложение в теории Меркурия». Астрономический журнал. 14: 49–51. Bibcode:1894AJ ..... 14 ... 49H. Дои:10.1086/102055.
37. Le Verrier UJJ (1859 г.). "Теория движения Меркурия". Annales de l'Observatoire Impérial de Paris. 5: 1–196, особенно. 98–106. Bibcode:1859АнПар ... 5 .... 1л.
    Саймон Ньюкомб (1882 г.). «Обсуждение и результаты наблюдений за транзитами Меркурия с 1677 по 1881 год». Астрономические документы, подготовленные для использования в американских эфемеридах и морском альманахе. 1: 473. Bibcode:1882USNAO ... 1..363N.
38. Браун EW (1903). «О степени точности новой теории Луны». Ежемесячные уведомления Королевского астрономического общества. 64: 524–534. Bibcode:1904МНРАС..64..524.. Дои:10.1093 / минрас / 64.6.524.
39. Розевир Н. (1982). Перигелий Меркурия от Леверье до Эйнштейна. Оксфорд.
40. Симон К.Р. (1971). Механика (3-е изд.). Ридинг, Массачусетс: Аддисон – Уэсли. С. 267 (Глава 6, проблема 7). ISBN  0-201-07392-7.
41. Чандрасекар, стр. 183–192.
42. Чандрасекхар, стр. 184.
43. Чандрасекар, стр. 67–70.
44. Чандрасекхар, стр. 187.
45. Уиттакер, стр. 83.

Библиография

• Ньютон I (1999) [1726]. Принципы: математические основы естественной философии. Переведено И. Бернард Коэн; Энн Уитман; Юлия Буденц (3-е изд.). Беркли, Калифорния: Калифорнийский университет Press. С. 147–148, 246–264, 534–545. ISBN  978-0-520-08816-0.
• Чандрасекхар С. (1995), Принципы Ньютона для обычного читателя, Oxford University Press, стр. 183–200, ISBN  978-0-19-852675-9
• Парс, Л.А. (1965). Трактат по аналитической динамике. Джон Уайли и сыновья. п. 56. ISBN  978-0-918024-07-7. LCCN  64024556.
• Whittaker ET (1937). Трактат об аналитической динамике частиц и твердых тел с введением в проблему трех тел (4-е изд.). Нью-Йорк: Dover Publications. п. 83. ISBN  978-0-521-35883-5.
• Routh EJ (1960). Трактат о динамике частицы (перепечатка изд. 1898 г.). Нью-Йорк: Dover Publications. С. 230–233 (разделы §356–359). ISBN  978-0-548-96521-4.
• Роуз Болл WW (1893). Очерк «Начала» Ньютона. Macmillan and Co. (перепечатка, Merchant Books). С. 84–85. ISBN  978-1-60386-012-3.
• Хейлброн, Дж. (2005), Оксфордское руководство по истории физики и астрономии, Oxford University Press, США, Bibcode:2005огп.книга ..... H, ISBN  978-0-19-517198-3
• Фитцпартрик, Ричард (2012), Введение в небесную механику, Издательство Кембриджского университета, ISBN  978-1-107-02381-9
• Ламбурн, Роберт (2010), Относительность, гравитация и космология, Издательство Кембриджского университета, ISBN  978-0-521-13138-4
• Гроссман, Натаниэль (1996), Настоящая радость небесной механики, Springer Science & Business Media, ISBN  978-0-8176-3832-0
• Шикин, Евгений (1995), Справочник и Атлас кривых, CRC Press, ISBN  978-0-8493-8963-4
• Лоуренс, Дж. Деннис (1972), Каталог специальных плоских кривых, Нью-Йорк: Дувр, ISBN  0486602885
• Вайсштейн, Эрик (2002), CRC Краткая энциклопедия математики, второе издание, CRC Press, ISBN  978-1-4200-3522-3

дальнейшее чтение

• Бертран Дж. (1873 г.). "Теорема относительна к движению единой точки вокруг неподвижного центра". Comptes rendus hebdomadaires des séances de l'Académie des Sciences. xxvii / 10: 849–853. (séance du lundi 20 октября 1873 г.)
• Коэн ИБ (1999). "Путеводитель по Ньютону Principia". Принципы: математические основы естественной философии. Беркли, Калифорния: Калифорнийский университет Press. С. 147–148, 246–252. ISBN  978-0-520-08816-0.
• Повар А. (1988). Движение Луны. Бристоль: Адам Хильгер. ISBN  0-85274-348-3.
• Д'Элизео, М.М. (2007). «Орбитальное уравнение первого порядка». Американский журнал физики. 75 (4): 352–355. Bibcode:2007AmJPh..75..352D. Дои:10.1119/1.2432126.
• Гвиччардини, Никколо (1999). Чтение Принципов: дебаты о математических методах Ньютона для натурфилософии с 1687 по 1736 год. Издательство Кембриджского университета. ISBN  978-0-521-54403-0.
• Ньютон I (1966). Principia Vol. I Движение тел (на основе 2-го издания Ньютона (1713 г.); переведено Эндрю Моттом (1729 г.) и отредактировано Флориан Каджори (1934) изд.). Беркли, Калифорния: Калифорнийский университет Press. стр.135–147 (Раздел IX Книги I). ISBN  978-0-520-00928-8. Альтернативный перевод более раннего (2-го) издания книги Ньютона. Principia.
• Смит Г.Е. (1999). «Ньютон и проблема движения Луны». Принципы: математические основы естественной философии. Беркли, Калифорния: Калифорнийский университет Press. С. 252–257. ISBN  978-0-520-08816-0.
• Смит Г.Е. (1999). «Движение лунной апсиды». Принципы: математические основы естественной философии. Беркли, Калифорния: Калифорнийский университет Press. С. 257–264. ISBN  978-0-520-08816-0.
• Спивак Михаил (1994). «Планетарное движение». Исчисление (3-е изд.). Опубликовать или погибнуть. ISBN  0-914098-89-6.

внешняя ссылка

• Проблема трех тел обсуждается Аленом Шенсинером на Scholarpedia