Музыкальная акустика - Musical acoustics
Музыкальная акустика или же музыкальная акустика это мультидисциплинарная область, объединяющая знания из физики[1][2][3], психофизика[4], органология [5](классификация инструментов), физиология[6], теория музыки[7], этномузыкология[8], обработка сигналов и приборостроение[9], среди других дисциплин. Как филиал акустика, он занимается исследованием и описанием физики Музыка - как звуки используются для создания музыки. Примеры областей обучения - функции музыкальные инструменты, то человеческий голос (физика речь и пение ), компьютерный анализ мелодия, а также в клиническом использовании музыки в музыкальная терапия.
Пионером музыкальной акустики был Герман фон Гельмгольц, немецкий эрудит XIX века, влиятельный врач, физик , физиолог, музыкант, математик и философ. Его книга Об ощущениях тона как физиологической основе теории музыки [7] представляет собой революционный сборник нескольких исследований и подходов, которые открыли совершенно новый взгляд на теория музыки, Музыкальный спектакль, музыкальная психология и физическое поведение музыкальных инструментов.
Методы и направления обучения
- В физика из музыкальные инструменты
- Частотный диапазон музыки
- Анализ Фурье
- Компьютер анализ музыкальной структуры
- Синтез музыкальных звуков
- Музыкальное познание, основанный на физике (также известный как психоакустика )
Физические аспекты
Когда одновременно воспроизводятся две разные высоты звука, их звуковые волны взаимодействуют друг с другом - максимумы и минимумы давления воздуха усиливают друг друга, создавая другую звуковую волну. Любая повторяющаяся звуковая волна, которая не является синусоидальной, может быть смоделирована множеством различных синусоидальных волн соответствующих частот и амплитуд ( частотный спектр ). В люди в слушание аппарат (в составе уши и мозг ) обычно может выделить эти тона и отчетливо их услышать. Когда одновременно воспроизводятся два или более тона, изменение давления воздуха в ухе «содержит» высоту каждого тона, а ухо и / или мозг выделяют и декодируют их в отдельные тона.
Когда исходные источники звука идеально периодичны, Примечание состоит из нескольких связанных синусоид (которые математически складываются друг с другом), называемых фундаментальный и гармоники, частичные, или же обертоны. Звуки гармонический частотные спектры. Самая низкая из присутствующих частот - это основная частота, на которой колеблется вся волна. Обертоны вибрируют быстрее, чем основная частота, но должны колебаться с целым числом, кратным основной частоте, чтобы общая волна была точно такой же в каждом цикле. Настоящие инструменты близки к периодическим, но частоты обертонов немного неидеальны, поэтому форма волны немного меняется со временем.[нужна цитата ]
Субъективные аспекты
Вариации в воздуха давление против ухо барабан и последующая физическая и неврологическая обработка и интерпретация вызывают субъективный опыт, называемый звук. Большинство звуков, которые люди узнают как музыкальный преобладают периодический или регулярные колебания, а не непериодические; то есть музыкальные звуки обычно имеют определенная подача. Передача этих вариаций по воздуху происходит через звук. волна. В очень простом случае звук синусоидальная волна, который считается базовой моделью звуковой волны, вызывает регулярное увеличение и уменьшение давления воздуха и воспринимается как очень чистый тон. Чистые тона могут быть получены камертоны или же свист. Скорость, с которой колеблется давление воздуха, - это частота тона, который измеряется в колебаниях в секунду, называется герц. Частота - это основной фактор, определяющий воспринимаемое подача. Частота музыкальных инструментов может меняться с высотой из-за изменений давления воздуха.
Диапазоны высоты звука музыкальных инструментов

*Эта диаграмма отображается только до C0, хотя некоторые органы, такие как Орган аудитории Boardwalk Hall, продолжаются до C−1 (на октаву ниже C0). Кроме того, основная частота субконтрабасовая туба это б♭−1.
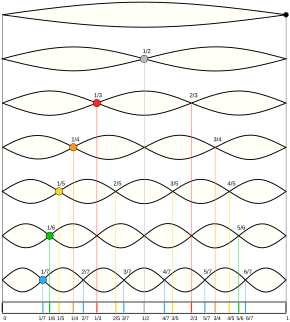
Гармоники, частичные и обертоны
В фундаментальный - частота, с которой колеблется вся волна. Обертоны - это другие синусоидальные компоненты, присутствующие на частотах выше основной. Все частотные компоненты, составляющие общую форму волны, включая основную частоту и обертоны, называются частичные. Вместе они образуют гармонический ряд.
Обертоны, которые являются точными целыми числами, кратными фундаментальному, называются гармоники. Когда обертон близок к гармоническому, но не точен, его иногда называют гармонической партией, хотя их часто называют просто гармониками. Иногда создаются обертоны, которые далеко не гармоничны, их просто называют частичными или негармоническими обертонами.
Основная частота считается первая гармоника и первая частичная. В этом случае нумерация парциальных частот и гармоник обычно одинакова; вторая частичка - вторая гармоника и т. д. Но если есть негармонические частички, нумерация перестает совпадать. Обертоны нумеруются по мере появления над фундаментальный. Строго говоря, первый обертон - это второй частичный (и обычно второй гармонический). Поскольку это может привести к путанице, только гармоники обычно обозначаются их номерами, а обертоны и частичные компоненты описываются их отношениями к этим гармоникам.
Гармоники и нелинейности

Когда периодическая волна состоит из основной и только нечетных гармоник (f, 3f, 5f, 7f, ...), суммарная волна равна полуволна симметричный; его можно инвертировать и сдвигать по фазе, и он будет точно таким же. Если волна имеет четные гармоники (0f, 2f, 4f, 6f, ...), она асимметрична; верхняя половина не является зеркальным отражением нижней.
И наоборот, система, изменяющая форму волны (помимо простого масштабирования или сдвига), создает дополнительные гармоники (гармоническое искажение ). Это называется нелинейный система. Если он воздействует на волну симметрично, все гармоники будут нечетными. Если это влияет на гармоники асимметрично, создается по крайней мере одна четная гармоника (и, вероятно, также нечетные гармоники).
Гармония
Если одновременно играются две ноты, с частотой соотношения которые являются простыми дробями (например, 2/1, 3/2 или 5/4), составная волна по-прежнему периодична с коротким периодом, а комбинация звучит согласный звук. Например, нота вибрирует с частотой 200 Гц, а нота - с частотой 300 Гц ( идеальный пятый, или соотношение 3/2 выше 200 Гц) сложите вместе, чтобы получилась волна, которая повторяется с частотой 100 Гц: каждые 1/100 секунды волна 300 Гц повторяется три раза, а волна 200 Гц повторяется дважды. Обратите внимание, что общая волна повторяется с частотой 100 Гц, но на самом деле синусоидальной составляющей 100 Гц нет.
Кроме того, в этих двух нотах много одинаковых частей. Например, у банкноты с основной частотой 200 Гц есть гармоники: (200,) 400, 600, 800, 1000, 1200,…
Нота с основной частотой 300 Гц имеет гармоники на:: (300,) 600, 900, 1200, 1500,… Две ноты имеют общие гармоники на 600 и 1200 Гц, и больше совпадают в дальнейшем по серии.
Комбинация составных волн с короткими основными частотами и общими или тесно связанными частями - вот что вызывает ощущение гармонии. Когда две частоты близки к простой доле, но не точны, составная волна циклически меняется достаточно медленно, чтобы слышать подавление волн как устойчивую пульсацию вместо тона. Это называется избиение, и считается неприятным, или диссонирующий.
Частота биений рассчитывается как разница между частотами двух нот. В приведенном выше примере | 200 Гц - 300 Гц | = 100 Гц. В качестве другого примера, комбинация 3425 Гц и 3426 Гц будет биться один раз в секунду (| 3425 Гц - 3426 Гц | = 1 Гц). Это следует из модуляция теория.
Разница между консонансом и диссонансом четко не определена, но чем выше частота биений, тем больше вероятность диссонанса интервала. Гельмгольца предположил, что максимальный диссонанс возникнет между двумя чистыми тонами при частоте биений примерно 35 Гц. [1]
Напольные весы
Материал музыкальной композиции обычно берется из набора нот, известного как шкала. Потому что большинство людей не могут адекватно определить абсолютный частот, идентичность шкалы заключается в соотношениях частот между ее тонами (известными как интервалы ).
В диатоническая шкала появляется в письменной форме на протяжении всей истории, состоящей из семи тонов в каждом октава. В просто интонация диатоническая гамма может быть легко построена с использованием трех простейших интервалов в октаве: идеальный пятый (3/2), идеальный четвертый (4/3), а большая треть (5/4). Поскольку формы пятого и третьего естественно присутствуют в серия обертонов гармонических резонаторов, это очень простой процесс.
В следующей таблице показаны соотношения между частотами всех нот справедливой музыки. крупный масштаб и фиксированная частота первой ноты гаммы.
| C | D | E | F | грамм | А | B | C |
|---|---|---|---|---|---|---|---|
| 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 |
Есть и другие гаммы, доступные только через интонацию, например малая шкала. Весы, которые не придерживаются только интонации, а вместо этого имеют интервалы, скорректированные для удовлетворения других потребностей, называются темпераменты, из которых равный темперамент является наиболее часто используемым. Темпераменты, хотя и скрывают акустическую чистоту только интервалов, часто обладают желательными свойствами, такими как замкнутость. круг пятых.
Рекомендации
- ^ Бенаде, Артур Х. (1990). Основы музыкальной акустики. Dover Publications. ISBN 9780486264844.
- ^ Fletcher, Neville H .; Россинг, Томас (2008-05-23). Физика музыкальных инструментов. Springer Science & Business Media. ISBN 9780387983745.
- ^ Кэмпбелл, Мюррей; Greated, Клайв (1994-04-28). Путеводитель по акустике для музыкантов. ОУП Оксфорд. ISBN 9780191591679.
- ^ Родерер, Хуан (2009). Физика и психофизика музыки: введение (4-е изд.). Нью-Йорк: Springer-Verlag. ISBN 9780387094700.
- ^ Энрике, Луис Л. (2002). Акустическая музыка (на португальском). Fundação Calouste Gulbenkian. ISBN 9789723109870.
- ^ Уотсон, Лэнхэм, Алан Х. Д., ML (2009). Биология музыкального исполнения и травмы, связанные с исполнением. Кембридж: Scarecrow Press. ISBN 9780810863590.
- ^ а б Гельмгольц, Герман Л. Ф .; Эллис, Александр Дж. (1885). "Об ощущениях тона как физиологической основе теории музыки Германа Л. Ф. Гельмгольца". Кембриджское ядро. Получено 2019-11-04.
- ^ Картоми, Маргарет (1990). О понятиях и классификациях музыкальных инструментов. Чикаго: Издательство Чикагского университета. ISBN 9780226425498.
- ^ Хопкин, Барт (1996). Дизайн музыкальных инструментов: практическая информация по дизайну инструментов. См. Sharp Press. ISBN 978-1884365089.
Смотрите также
- Акустический резонанс
- Киматика
- Математика музыкальных гамм
- Струнный резонанс
- Вибрирующая струна
- 3-й мост (гармонический резонанс на основе равного разделения струн)
- Основы физики скрипки
внешняя ссылка
- Музыкальная акустика - звуковые файлы, анимация и иллюстрации - University of New South Wales
- Коллекция акустики - описания, фото и видеоклипы аппарата для исследований в музыкальной акустике проф. Дейтон Миллер
- Технический комитет по музыкальной акустике (TCMU) Американского акустического общества (ASA)
- Библиотека исследований музыкальной акустики (MARL)
- Acoustics Group / Курсы по акустике и музыкальным технологиям - Эдинбургский университет
- Группа акустических исследований - Открытый университет
- Группа музыкальной акустики Speech, Music and Hearing KTH
- Физика звука клавесина
- Визуальная музыка
- Savart Journal - Интернет-журнал открытого доступа по науке и технологиям струнных музыкальных инструментов.
- Онлайн-курс Audio Engineering под Creative Commons Лицензия
- Интерференция и созвучие из Physclips
- Curso de Acústica Musical (Испанский)