Звенящие артефакты - Ringing artifacts

Внешний образ
	Графики импульсной и частотной характеристики фильтра Баттерворта

Изображение с артефактами звона. 3 уровня на каждой стороне перехода: перерегулирование, первое кольцо и (слабое) второе кольцо.

То же изображение без звенящих артефактов.

В обработка сигналов, особенно цифровая обработка изображений, звенящие артефакты находятся артефакты которые проявляются как ложные сигналы возле резких переходов в сигнале. Визуально они выглядят как полосы или «призраки» по краям; слышно, они выглядят как "эхо" рядом с переходные процессы, особенно звуки из ударные инструменты; наиболее заметны предварительное эхо. Термин «звон» объясняется тем, что выходной сигнал колеблется со скоростью затухания вокруг резкого перехода на входе, аналогично колокол после удара. Как и в случае с другими артефактами, их минимизация является критерием конструкция фильтра.

Вступление

Основная причина появления артефактов звонка - превышение и колебания в пошаговая реакция фильтра.

Основная причина артефактов звонка связана с тем, что сигнал ограниченный диапазон (в частности, не имеющие высоких частот) или прошедшие через фильтр нижних частот; это частотная область описание. область времени, причиной такого звонка является рябь на функция sinc,^[1] какой импульсивный ответ (представление во временной области) идеального фильтра нижних частот. Математически это называется Феномен Гиббса.

Можно различить превышение (и недолет), возникающий при усилении переходов - выход выше входного - от звонка, где после перерегулирование, сигнал перекомпенсируется и теперь ниже целевого значения; эти явления часто возникают вместе, поэтому их часто объединяют и вместе называют «звонком».

Термин «звон» чаще всего используется для обозначения ряби в время домен, хотя он также иногда используется для частота эффекты домена:^[2]оконное использование фильтра во временной области с помощью прямоугольной функции вызывает рябь в частота по той же причине, что и фильтр нижних частот для кирпичной стены (прямоугольная функция в частота домен) вызывает рябь в время области, в каждом случае преобразование Фурье прямоугольной функции является функцией sinc.

Есть связанные артефакты, вызванные другими частотная область эффекты и похожие артефакты по не связанным причинам.

Причины

Описание

В функция sinc, то импульсивный ответ для идеального фильтр нижних частот, иллюстрирующий вызов импульса.

В Феномен Гиббса, иллюстрирующий звонок для ступенчатая функция.

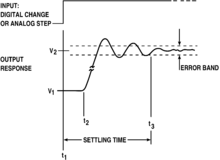
По определению, звонок возникает, когда не колеблющийся вход дает колебательный выход: формально, когда входной сигнал монотонный на интервале имеет выходную характеристику, которая не является монотонной. Наиболее серьезно это происходит, когда импульсивный ответ или же пошаговая реакция из фильтр имеет колебания - менее формально, если для импульсного входа, соответственно ступенчатого входа (резкий переход), на выходе есть выпуклости. Звонок чаще всего относится к ступенчатому звону, и на этом будет основное внимание.

Звон тесно связан с превышение и недобор, когда выходной сигнал принимает значения выше максимального (соответственно ниже минимального) входного значения: одно может быть без другого, но в важных случаях, таких как фильтр нижних частот, сначала наблюдается выброс, затем реакция возвращается ниже установившегося уровня, вызывая первое кольцо, а затем колеблется назад и вперед выше и ниже установившегося уровня. Таким образом, перерегулирование - это первая ступень явления, а звон - вторая и последующие ступени. Из-за этой тесной связи термины часто объединяются, причем «звон» относится как к начальному выбросу, так и к последующим звонкам.

Если есть линейный инвариант во времени (LTI) фильтр, то можно понять фильтр и звон в терминах импульсной характеристики (представление во временной области) или в терминах его преобразования Фурье, частотный отклик (просмотр в частотной области). Звонок - это время артефакт домена, а в конструкция фильтра уступает место желаемым характеристикам частотной области: желаемая частотная характеристика может вызвать звон, в то время как уменьшение или устранение звонка может ухудшить частотную характеристику.

sinc фильтр

В Интеграл синуса для положительных значений, демонстрирующих колебания.

Центральный пример, и часто то, что подразумевается под «звенящими артефактами», - это идеальный (кирпичная стена ) фильтр нижних частот, то sinc фильтр. У этого есть колебательная импульсная функция отклика, как показано выше, и ступенчатая характеристика - ее интеграл, интеграл синуса - таким образом, также есть колебания, как показано справа.

Эти артефакты звонка не являются результатом несовершенной реализации или работы с окнами: идеальный фильтр нижних частот, обладая желаемой частотной характеристикой, обязательно вызывает артефакты звонка в время домен.

Область времени

Что касается импульсной характеристики, соответствие между этими артефактами и поведением функции выглядит следующим образом:

недостижение импульса эквивалентно импульсной характеристике, имеющей отрицательные значения,
импульсный звон (звон около точки) в точности эквивалентен импульсной характеристике с колебаниями, которая эквивалентна производной импульсной характеристики, чередующейся между отрицательными и положительными значениями,
и отсутствует понятие выброса импульса, поскольку предполагается, что единичный импульс имеет бесконечную высоту (и интеграл 1 - a Дельта-функция Дирака ), и поэтому не может быть недооценен.

Переходя к ступенчатой характеристике, ступенчатая характеристика является интегралом импульсивный ответ; формально значение переходной характеристики в момент времени а это интеграл ${displaystyle int _ {- infty} ^ {a}}$ импульсной характеристики. Таким образом, значения переходной характеристики можно понять с точки зрения хвост интегралы импульсного отклика.

Предположим, что общий интеграл импульсной характеристики равен 1, поэтому он отправляет постоянный вход на ту же константу, что и выход - в противном случае фильтр имеет прирост, а масштабирование по усилению дает интеграл 1.

Ступенчатый недолет эквивалентен отрицательному значению хвостового интеграла, и в этом случае величина недорегулирования является значением хвостового интеграла.
Ступенчатый выброс эквивалентен хвостовому интегралу, превышающему 1, и в этом случае величина выброса - это величина, на которую хвостовой интеграл превышает 1 - или, что эквивалентно, значение хвоста в другом направлении, ${displaystyle int _ {a} ^ {infty},}$ так как они в сумме составляют 1.
Ступенчатый звон эквивалентен чередованию хвостовых интегралов между возрастающими и убывающими - взятие производных эквивалентно импульсной характеристике, чередующейся между положительными и отрицательными значениями.^[3] Области, где импульсная характеристика ниже или выше Икс-оси (формально области между нулями) называются доли а величина колебания (от пика до впадины) равна интегралу соответствующего лепестка.

Импульсный отклик может иметь много отрицательных лепестков и, следовательно, много колебаний, каждое из которых дает кольцо, хотя они затухают для практических фильтров, и, таким образом, обычно можно увидеть только несколько колец, причем первое обычно наиболее выражено.

Обратите внимание, что если импульсный отклик имеет небольшие отрицательные лепестки и большие положительные лепестки, то он будет демонстрировать звон, но не перерегулирование или перерегулирование: интеграл хвоста всегда будет между 0 и 1, но будет колебаться вниз на каждом отрицательном лепестке. Однако в фильтре sinc лепестки монотонно уменьшаются по величине и чередуются по знаку, как в фильтре переменный гармонический ряд, и, таким образом, хвостовые интегралы также меняют знак, поэтому он демонстрирует выбросы, а также звон.

И наоборот, если импульсная характеристика всегда неотрицательна, поэтому у нее нет отрицательных лепестков - функция является распределение вероятностей - тогда ступенчатая характеристика не будет показывать ни звона, ни перерегулирования, ни недорега - это будет монотонная функция, возрастающая от 0 до 1, как кумулятивная функция распределения. Таким образом, основным решением с точки зрения временной области является использование фильтров с неотрицательной импульсной характеристикой.

Частотный диапазон

Перспектива частотной области такова, что звон вызывается резкой границей в прямоугольной области. полоса пропускания в частотной области и, таким образом, уменьшается за счет более плавного скатывание, как описано ниже.^[1]^[4]

Решения

Решения зависят от параметров проблемы: если причиной является фильтр нижних частот, можно выбрать другую конструкцию фильтра, которая уменьшает артефакты за счет снижения производительности в частотной области. С другой стороны, если причиной является сигнал с ограниченной полосой пропускания, как в JPEG, нельзя просто заменить фильтр, и артефакты звонка могут оказаться трудными для исправления - они присутствуют в JPEG 2000 и многие кодеки сжатия звука (в виде предварительное эхо ), как обсуждается в Примеры.

Фильтр нижних частот

В Функция Гаусса неотрицательна и не колеблется, поэтому не вызывает перерегулирования или звона.

Если причиной является использование кирпичного фильтра нижних частот, можно заменить фильтр фильтром, который уменьшает артефакты во временной области за счет производительности в частотной области. Это можно проанализировать с точки зрения временной или частотной области.

Во временной области причиной является импульсная характеристика, которая колеблется, принимая отрицательные значения. Эту проблему можно решить, используя фильтр, импульсная характеристика которого неотрицательна и не колеблется, но разделяет желаемые характеристики. Например, для фильтра нижних частот Гауссов фильтр неотрицательна и не колеблется, следовательно, не вызывает звонка. Однако он не так хорош, как фильтр нижних частот: он скатывается в полосе пропускания и просачивается в полосе пропускания. полоса задерживания: с точки зрения изображения, фильтр Гаусса «размывает» сигнал, что отражает ослабление желаемых более высокочастотных сигналов в полосе пропускания.

Общее решение - использовать оконная функция на синк-фильтре, который отсекает или уменьшает отрицательные лепестки: они соответственно устраняют и уменьшают выбросы и звон. Обратите внимание, что усечение некоторых, но не всех лепестков устраняет звон за пределами этой точки, но не уменьшает амплитуду звонка, который не усекается (поскольку это определяется размером лепестка), и увеличивает величину выброса если последний невырезанный лепесток отрицательный, поскольку величина выброса является интегралом хвост, который больше не отменяется положительными долями.

Кроме того, в практических реализациях один, по крайней мере, усекает sinc, в противном случае нужно использовать бесконечно много точек данных (или, скорее, все точки сигнала) для вычисления каждой точки вывода - усечение соответствует прямоугольному окну и делает фильтр практически реализуемым , но частотная характеристика уже не идеальна.^[5]Фактически, если взять фильтр нижних частот кирпичной стены (sinc во временной области, прямоугольный в частотной области) и усечь его (умножить на прямоугольную функцию во временной области), это сворачивает частотную область с sinc (преобразование Фурье прямоугольная функция) и вызывает звон в частота домен,^[2] который упоминается как рябь. В символах ${displaystyle {mathcal {F}} (mathrm {sinc} cdot mathrm {rect}) = mathrm {rect} * mathrm {sinc}.}$ Частотный звон в полосе задерживания также называют боковые доли. Желателен ровный отклик в полосе пропускания, поэтому одно окно с функциями, преобразование Фурье которых имеет меньше колебаний, поэтому поведение в частотной области лучше.

Умножение во временной области соответствует свертке в частотной области, поэтому умножение фильтра на оконную функцию соответствует свертке преобразования Фурье исходного фильтра с преобразованием Фурье окна, что имеет эффект сглаживания - таким образом, оконное отображение во времени соответствует сглаживанию в частотной области и снижает или устраняет выбросы и звон.^[6]

в частотная область Причина может быть истолкована как из-за резкого отсечения (кирпичная стена) и уменьшения звона за счет использования фильтра с более плавным спадом.^[1] Так обстоит дело с фильтром Гаусса, величина которого Сюжет Боде представляет собой открывающуюся вниз параболу (квадратичный спад), так как ее преобразование Фурье снова гауссово, следовательно (с точностью до масштаба) ${displaystyle e ^ {- x ^ {2}}}$ - логарифм доходности ${displaystyle -x ^ {2}.}$

В электронные фильтры компромисс между откликом в частотной области и артефактами звонка во временной области хорошо иллюстрируется Фильтр Баттерворта: частотная характеристика фильтра Баттерворта линейно убывает по логарифмической шкале, а фильтр первого порядка имеет крутизну -6 дБ на октава, фильтр второго порядка –12 дБ на октаву и пфильтр-го порядка, имеющий наклон ${displaystyle -6n}$ дБ на октаву - в пределе приближается к каменному фильтру. Таким образом, среди них фильтр первого порядка спадает медленнее всего и, следовательно, демонстрирует наименьшее количество артефактов во временной области, но больше всего дает утечку в полосе задерживания, тогда как по мере увеличения порядка утечка уменьшается, но артефакты увеличиваются.^[4]

Преимущества

Увеличивается искусственно добавленный выброс вокруг левой полосы острота.

В то время как артефакты звона обычно считаются нежелательными, начальный выброс (ореол) при переходах увеличивается. острота (кажущаяся резкость) за счет увеличения производной по переходу, и, таким образом, может рассматриваться как улучшение.^[8]

Связанные явления

Перескок

Функция sinc имеет отрицательные хвостовые интегралы, следовательно, имеет перерегулирование.

Двухлепестковый фильтр Ланцоша показывает только выбросы, тогда как трехлопастный фильтр демонстрирует выбросы и звенящие сигналы.

Другой артефакт превышение (и недолет), что проявляется не кольцами, а повышенным скачком при переходе. Это связано с звонком и часто возникает в сочетании с ним.

Перерегулирование и недолёт вызваны отрицательным хвостом - в sinc интеграл от первого нуля до бесконечности, включая первый отрицательный лепесток. Звонок вызван следующими причинами. положительный tail - в sinc интеграл от второго нуля до бесконечности, включая первый нецентральный положительный лепесток. необходимо для звонка,^{[сомнительный – обсуждать]} но может встречаться отдельно: например, двухлопастная Фильтр Ланцоша имеет только один отрицательный лепесток с каждой стороны, без следующего положительного лепестка, и, таким образом, демонстрирует перерегулирование, но без звона, в то время как 3-лепестковый фильтр Ланцоша демонстрирует как перерегулирование, так и звенящий сигнал, хотя оконное управление уменьшает это по сравнению с фильтром sinc или усеченным sinc фильтр.

Аналогично, ядро свертки, используемое в бикубическая интерполяция подобен двухлепестному оконному синхроимпульсу, принимает отрицательные значения и, таким образом, создает артефакты перерегулирования, которые появляются в виде ореолов при переходах.

Вырезка

Следствием перерегулирования и недорега является вырезка.Если сигнал ограничен, например, 8-битным или 16-битным целым числом, это перерегулирование или недорегулирование может выйти за пределы диапазона допустимых значений, что приведет к ограничению.

Строго говоря, ограничение вызвано комбинацией перерегулирования и ограниченной числовой точности, но оно тесно связано со звоном и часто возникает в сочетании с ним.

Ограничение также может происходить по не связанным причинам, когда сигнал просто выходит за пределы диапазона канала.

С другой стороны, отсечение можно использовать для скрытия звона на изображениях. Некоторые современные кодеки JPEG, такие как mozjpeg и ISO libjpeg используйте такой трюк, чтобы уменьшить звон, намеренно вызывая выбросы в результатах IDCT.^[9] Эта идея возникла в патче mozjpeg.^[10]

Звон и рябь

Амплитудно-частотная характеристика 5-го порядка Фильтр Чебышева, выставляя рябь.

В обработке сигналов и связанных областях общее явление колебаний во временной области называется звон, в то время как колебания в частотной области обычно называют рябь, правда вообще не "рябь".

Ключевым источником пульсаций в цифровой обработке сигналов является использование оконные функции: если взять бесконечный импульсный отклик (IIR) фильтр, такой как фильтр sinc, и окна его, чтобы он конечная импульсная характеристика, как в метод оформления окна, тогда частотная характеристика результирующего фильтра представляет собой свертку частотной характеристики БИХ-фильтра с частотной характеристикой оконной функции. Примечательно, что частотная характеристика прямоугольного фильтра является функцией sinc (прямоугольная функция и функция sinc являются Двойственный Фурье друг к другу), и, таким образом, усечение фильтра во временной области соответствует умножению на прямоугольный фильтр, таким образом, свертка с помощью sinc-фильтра в частотной области вызывает пульсации. В символах частотная характеристика ${displaystyle mathrm {rect} (t) cdot h (t)}$ является ${displaystyle mathrm {sinc} (t) * {hat {h}} (t).}$ В частности, усечение самой функции sinc дает ${displaystyle mathrm {rect} (t) cdot mathrm {sinc} (t)}$ во временной области, и ${displaystyle mathrm {sinc} (t) * mathrm {rect} (t)}$ в частотной области, так же как фильтрация нижних частот (усечение в частотной области) вызывает звон во временной области, усечение во временной области (оконное управление прямоугольным фильтром) вызывает рябь в частотной области.

Примеры

JPEG

Экстремальный пример артефактов JPEG, включая звон: голубые (= белый минус красный) кольца вокруг красной звезды.

Дискретное косинусное преобразование базисные функции.

JPEG сжатие может привести к появлению артефактов звона при резких переходах, которые особенно заметны в тексте.

Это происходит из-за потери высокочастотных составляющих, например, при переходе на ступенчатый сигнал.JPEG использует блоки 8 × 8, на котором дискретное косинусное преобразование (DCT) выполняется. DCT - это Преобразование, связанное с Фурье, и звон возникает из-за потери высокочастотных компонентов или потери точности высокочастотных компонентов.

Они также могут возникать на краю изображения: поскольку JPEG разбивает изображения на блоки 8 × 8, если изображение не является целым числом блоков, край не может быть легко закодирован, и такие решения, как заполнение черной рамкой, создают резкий переход в источнике, отсюда звенящие артефакты в кодированном изображении.

Звон бывает и в вейвлет -основан JPEG 2000.

JPEG и JPEG 2000 имеют другие артефакты, как показано выше, например блокировку ("неровности ") и крайняя занятость ("москитный шум "), хотя это связано со спецификой форматов и не вызывает звонка, как описано здесь.

Некоторые иллюстрации:

Иллюстрированные артефакты базового формата JPEG и JPEG2000

Изображение	Сжатие без потерь	Сжатие с потерями
Оригинал
Обработано Детектор Canny Edge, выделение артефактов.

Pre-echo

Pre-echo встречается в перкуссии, такой как тарелки.

В обработка аудиосигнала, звонок может вызвать появление эха до и после переходные процессы, например, импульсивный звук от ударные инструменты, Такие как тарелки (это импульс звонит). (причинный ) эхо после переходного процесса не слышно, потому что оно маскируется переходным процессом, эффект, называемый временная маскировка. Таким образом, только (антипричинный ) эхо до того, как будет слышен переходный процесс, и это явление называется предварительное эхо.

Это явление происходит как артефакт сжатия в алгоритмах сжатия звука, которые используют Преобразования, связанные с Фурье, Такие как MP3, AAC, и Vorbis.

Подобные явления

Другие явления имеют симптомы, похожие на звон, но в остальном различаются по своим причинам. В случаях, когда они вызывают круговые артефакты вокруг точечных источников, их можно называть «кольцами» из-за круглой формы (формально кольцо ), который не имеет отношения к феномену "звона" (колебательного затухания) частоты, обсуждаемому на этой странице.

Улучшение края

Улучшение края, который направлен на увеличение краев, может вызвать явление звона, особенно при многократном использовании, например, при использовании DVD-плеера, за которым следует телевизор. Это может быть сделано высоко-проходная фильтрация, а не фильтрация нижних частот.^[4]

Специальные функции

В Воздушный узор, вызванный Фраунгофера дифракция.

Много специальные функции демонстрируют колебательное затухание, и, таким образом, свертка с такой функцией дает звенящий сигнал на выходе; можно рассматривать эти звонки или ограничить термин непреднамеренными артефактами при обработке сигналов в частотной области.

Фраунгофера дифракция дает Диск Эйри в качестве функция разброса точки, имеющий шаблон звонка.

Немного Функции Бесселя первого рода с колебательным распадом.

В Функция Бесселя первого рода, ${displaystyle J_ {0},}$ что связано с Функция Эйри, проявляет такой распад.

Комбинации расфокусировать и сферическая аберрация экспонировать кольцевые артефакты.

В камерах комбинация расфокусировать и сферическая аберрация может давать круговые артефакты ("кольцевые" узоры). Однако структура этих артефактов не обязательно должна быть похожа на звон (как обсуждается на этой странице) - они могут демонстрировать колебательное затухание (круги с уменьшающейся интенсивностью) или другие образцы интенсивности, такие как одна яркая полоса.

Вмешательство

Привидение это форма телевизионные помехи где изображение повторяется. Хотя это не звонко, это может быть интерпретировано как свертка с функцией, которая равна 1 в начале координат и ε (интенсивность призрака) на некотором расстоянии, что формально аналогично приведенным выше функциям (один дискретный пик, скорее, чем непрерывное колебание).

Отблеск от линз

Отблеск от линз.

В фотографии отблеск от линз - это дефект, из-за которого вокруг светлых участков могут появляться различные круги, а также с призраками на фотографии из-за нежелательного света, например отражения и рассеивания элементов в объективе.

Визуальные иллюзии

Полосы Маха

Визуальные иллюзии могут возникать при переходах, как в Полосы Маха, которые по восприятию демонстрируют недостижение / перерегулирование, аналогичное явлению Гиббса.