Сверхтекучий гелий-4 - Superfluid helium-4
Сверхтекучий гелий-4 это сверхтекучий форма гелий-4, изотоп элемента гелий. Сверхтекучая жидкость - это состояние дела в котором материя ведет себя как жидкость с нуля вязкость. Вещество, которое выглядит как обычная жидкость, протекает без трения по любой поверхности, что позволяет ему продолжать циркуляцию через препятствия и поры в контейнерах, в которых оно находится, подчиняясь только собственному инерция.
Известный как важный аспект в изучении квантовая гидродинамика и макроскопические квантовые явления, то сверхтекучесть эффект был обнаружен Петр Капица[1] и Джон Ф. Аллен, и Дон Мизенер[2] в 1937 году. С тех пор он был описан через феноменологический и микроскопические теории. Как известно, образование сверхтекучей жидкости связано с образованием Конденсат Бозе – Эйнштейна. Об этом свидетельствует тот факт, что в жидкости возникает сверхтекучесть. гелий-4 при гораздо более высоких температурах, чем в гелий-3. Каждый атом гелий-4 это бозон частица, в силу ее нулевого спина. Гелий-3 однако это фермион частица, которая может образовывать бозоны, только спариваясь сама с собой при гораздо более низких температурах, в процессе, аналогичном спариванию электронов в сверхпроводимость.[3]
В 1950-х Холл и Винен провели эксперименты, установившие существование квантованный вихрь линии в сверхтекучем гелии.[4] В 1960-х Рейфилд и Рейф установили существование квантованных вихревых колец.[5] Паккард наблюдал пересечение вихревых линий со свободной поверхностью жидкости,[6]и Авенель и Вароко изучали Эффект джозефсона в сверхтекучем гелии-4.[7] В 2006 году группа из Университета Мэриленда визуализировала квантованные вихри с помощью небольших трассерных частиц твердый водород.[8]
Характеристики
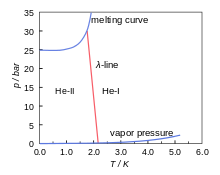


Рисунок 1 - это фазовая диаграмма из 4Он.[9] Это диаграмма давление-температура (p-T), показывающая твердые и жидкие области, разделенные кривой плавления (между жидким и твердым состоянием), и жидкую и газовую области, разделенные линией давления пара. Последний заканчивается критическая точка где пропадает разница между газом и жидкостью. На диаграмме показано замечательное свойство: 4Он жидкий даже при абсолютный ноль. 4Он прочен только при давлении выше 25 бар.
На рисунке 1 также показана λ-линия. Это линия, разделяющая две жидкие области на фазовой диаграмме, обозначенной He-I и He-II. В области He-I гелий ведет себя как обычная жидкость; в области He-II гелий сверхтекучий.
Название «лямбда-линия» происходит от графика удельной теплоемкости - температуры, имеющего форму греческой буквы λ.[10][11] См. Рисунок 2, на котором показан пик при 2,172 К, так называемая λ-точка 4Он.
Ниже лямбда-линии жидкость может быть описана так называемой двухжидкостной моделью. Он ведет себя так, как если бы он состоит из двух компонентов: нормального компонента, который ведет себя как обычная жидкость, и сверхтекучего компонента с нулевой вязкостью и нулевой энтропией. Соотношения соответствующих плотностей ρп/ ρ и ρs/ ρ, где ρп (ρs) плотность нормального (сверхтекучего) компонента и ρ (общая плотность) зависит от температуры и представлена на рисунке 3.[12] При понижении температуры доля сверхтекучей плотности увеличивается от нуля при Тλ до одного при нулевом кельвине. Ниже 1 К гелий почти полностью сверхтекучий.
Возможно создание волн плотности нормальной компоненты (и, следовательно, сверхтекучей компоненты, поскольку ρп + ρs = константа), которые похожи на обычные звуковые волны. Этот эффект называется второй звук. Из-за температурной зависимости ρп (рисунок 3) эти волны в ρп тоже температурные волны.


Фильм поток
Многие обычные жидкости, такие как спирт или нефть, ползут по твердым стенкам под действием их поверхностного натяжения. Жидкий гелий также обладает этим свойством, но в случае He-II течение жидкости в слое ограничивается не его вязкостью, а критической скоростью, которая составляет около 20 см / с. Это довольно высокая скорость, поэтому сверхтекучий гелий может относительно легко течь вверх по стенке контейнеров, через верх и вниз до того же уровня, что и поверхность жидкости внутри контейнера, в сифонном эффекте, как показано на рисунке 4. В контейнер, поднятый над уровнем жидкости, образует видимые капли, как показано на рисунке 5. Однако было замечено, что поток через нанопористую мембрану становится ограниченным, если диаметр пор составляет менее 0,7 нм (т.е. примерно в три раза больше классического диаметр атома гелия), предполагая, что необычные гидродинамические свойства He проявляются в большем масштабе, чем в классическом жидком гелии.[13]
Сверхтекучая гидродинамика
Уравнение движения сверхтекучей компоненты в несколько упрощенном виде[14] дается законом Ньютона
Масса M4 это молярная масса 4Он и - скорость сверхтекучей компоненты. Производная по времени - это так называемая гидродинамическая производная, то есть скорость увеличения скорости при движении с жидкостью. В случае сверхтекучей 4Он в гравитационном поле сила определяется выражением[15][16]
В этом выражении μ - молярный химический потенциал, грамм гравитационное ускорение и z вертикальная координата. Таким образом мы получаем
(1)
Уравнение(1) только если vs ниже определенного критического значения, которое обычно определяется диаметром проточного канала.[17][18]
В классической механике сила часто представляет собой градиент потенциальной энергии. Уравнение(1) показывает, что в случае сверхтекучей компоненты сила содержит член, связанный с градиентом химический потенциал. Отсюда замечательные свойства He-II, такие как эффект фонтана.



Давление фонтана
Чтобы переписать уравнение.(1) в более привычной форме воспользуемся общей формулой
(2)
Здесь Sм молярная энтропия и Vм молярный объем. С формулой.(2) μ (п,Т) можно найти путем интегрирования в плоскости p-T. Сначала мы проинтегрируем от начала координат (0,0) до (п, 0), поэтому при Т = 0. Далее интегрируем из (п, 0) до (п,Т), поэтому при постоянном давлении (см. рисунок 6). В первом интеграле dТ= 0, а во втором dп= 0. С формулой.(2) мы получаем
(3)
Нас интересуют только случаи, когда п маленький, так что Vм практически постоянный. Так
(4)
куда Vm0 молярный объем жидкости при Т = 0 и п = 0. Другой член в формуле.(3) также написано как продукт Vm0 и количество пж который имеет размерность давления
(5)
Давление пж называется фонтаном давления. Его можно рассчитать из энтропии 4Он, в свою очередь, можно рассчитать по теплоемкости. За Т =Тλ давление фонтана равно 0,692 бар. Плотностью жидкого гелия 125 кг / м3 и грамм = 9,8 м / с2 это соответствует столбу жидкого гелия высотой 56 метров. Итак, во многих экспериментах давление фонтана оказывает большее влияние на движение сверхтекучего гелия, чем сила тяжести.
С уравнениями.(4) и (5), Уравнение(3) получает форму
(6)
Подстановка уравнения.(6) в (1) дает
(7)
с ρ₀ = M4/Vm0 плотность жидкости 4Он при нулевом давлении и температуре.
Уравнение(7) показывает, что сверхтекучая компонента ускоряется градиентами давления и гравитационного поля, как обычно, а также градиентом давления фонтана.
Пока уравнение.(5) имеет только математическое значение, но в специальных экспериментальных условиях пж может проявиться как реальное давление. На рис. 7 показаны два сосуда, оба из которых содержат He-II. Предполагается, что на левом судне температура 0 градусов по Кельвину (Тл= 0) и нулевого давления (пл = 0). Сосуды связаны между собой так называемой сверхтекучей. Это трубка, заполненная очень мелким порошком, поэтому поток нормального компонента заблокирован. Однако сверхтекучая составляющая может без проблем проходить через эту сверхтеку (ниже критической скорости около 20 см / с). В устойчивом состоянии vs= 0, поэтому уравнение(7) подразумевает
(8)
где индекс l (r) относится к левой (правой) стороне сверхтока. В данном конкретном случае пл = 0, zл = zр, и пэт = 0 (поскольку Тл = 0). Как следствие,
Это означает, что давление в правом сосуде равно давлению фонтана при Тр.
В эксперименте, показанном на рисунке 8, можно создать фонтан. Эффект фонтана используется для стимулирования циркуляции 3Он в холодильниках.[19][20]

Тепловой транспорт
На рисунке 9 показан эксперимент теплопроводности между двумя температурами. ТЧАС и ТL соединены трубкой, заполненной He-II. Когда к горячему концу прикладывается тепло, на горячем конце повышается давление в соответствии с формулой.(7). Это давление перемещает нормальный компонент от горячего конца к холодному в соответствии с
(9)
Здесь ηп - вязкость нормального компонента,[21] Z некоторый геометрический фактор, и объемный расход. Нормальный поток уравновешивается потоком сверхтекучей компоненты от холодного конца к горячему. На концевых участках происходит нормальное преобразование в сверхтекучую и наоборот. Итак, тепло переносится не за счет теплопроводности, а за счет конвекции. Этот вид теплопередачи очень эффективен, поэтому теплопроводность He-II намного лучше, чем у лучших материалов. Ситуация сопоставима с тепловые трубы где тепло переносится за счет газожидкостной конверсии. Высокая теплопроводность He-II применяется для стабилизации сверхпроводящих магнитов, таких как Большой адронный коллайдер в ЦЕРН.
Теория
Двухжидкостной подход Ландау
Л. Д. Ландау Феноменологическая и полумикроскопическая теория сверхтекучести гелия-4 принесла ему Нобелевскую премию по физике в 1962 году. Предполагая, что звуковые волны являются наиболее важными возбуждениями в гелии-4 при низких температурах, он показал, что гелий-4, протекающий мимо стены не создавал бы спонтанного возбуждения, если бы скорость потока была меньше скорости звука. В этой модели скорость звука - это «критическая скорость», выше которой сверхтекучесть разрушается. (Гелий-4 на самом деле имеет меньшую скорость потока, чем скорость звука, но эта модель полезна для иллюстрации концепции.) Ландау также показал, что звуковая волна и другие возбуждения могут уравновешиваться друг с другом и течь отдельно от остального гелия. -4, который известен как «конденсат».
Затем по импульсу и скорости потока возбуждений он мог определить плотность «нормальной жидкости», которая равна нулю при нулевой температуре и увеличивается с температурой. При так называемой лямбда-температуре, где нормальная плотность жидкости равна общей плотности, гелий-4 больше не является сверхтекучим.
Чтобы объяснить первые данные о теплоемкости сверхтекучего гелия-4, Ландау постулировал существование типа возбуждения, которое он назвал "ротон ", но по мере того, как стали доступны более точные данные, он решил, что" ротон "был тем же самым, что и версия звука с большим импульсом.
Теория Ландау не развивает микроскопическую структуру сверхтекучей компоненты жидкого гелия.[22] Первые попытки создать микроскопическую теорию самой сверхтекучей компоненты были предприняты Лондоном.[23] а затем Тиса.[24][25]Другие микроскопические модели были предложены разными авторами. Их основная цель - получить форму межчастичного потенциала между атомами гелия в сверхтекучем состоянии из первых принципов квантовая механика На сегодняшний день предложен ряд моделей такого типа, в том числе: модели с вихревыми кольцами, модели твердых сфер и теории гауссовых кластеров.
Модель вихревого кольца
Ландау считал, что завихренность проникает в сверхтекучий гелий-4 через вихревые слои, но с тех пор было показано, что такие слои нестабильны.Ларс Онсагер и, позже независимо, Фейнман показал, что завихренность проникает через квантованные вихревые линии. Они также развили идею квантовый вихрь кольца.Арье Бейл в 1940-х,[26]и Ричард Фейнман около 1955 г.,[27] разработал микроскопические теории ротона, который вскоре был обнаружен Палевским в экспериментах с неупругими нейтронами. Позже Фейнман признал, что его модель дает только качественное согласие с экспериментом.[28][29]
Модели твердых сфер
В основе моделей лежит упрощенная форма межчастичного потенциала между атомами гелия-4 в сверхтекучей фазе. А именно, предполагается, что потенциал имеет тип твердых сфер.[30][31][32]В этих моделях качественно воспроизведен знаменитый спектр возбуждений Ландау (ротонный).
Гауссов кластерный подход
Это двухуровневый подход, описывающий сверхтекучую компоненту жидкого гелия-4. Он состоит из двух вложенные модели, связанные через параметрическое пространство. Коротковолновая часть описывает внутреннюю структуру жидкий элемент используя непертурбативный подход, основанный на Логарифмическое уравнение Шредингера; это предлагает Гауссовский -подобное поведение внутренней плотности элемента и потенциала межчастичного взаимодействия. Длинноволновая часть - это квантовая теория многих тел таких элементов, которая имеет дело с их динамикой и взаимодействием. Подход обеспечивает единое описание фонон, Максон и ротон возбуждения, и имеет примечательное согласие с экспериментом: с одним важным параметром, чтобы соответствовать, воспроизводит с высокой точностью спектр ротона Ландау, скорость звука и структурный фактор сверхтекучего гелия-4.[33]В этой модели используется общая теория квантовых бозе-жидкостей с логарифмическими нелинейностями.[34] который основан на введении диссипативный -типа вклад в энергию, связанный с квантовой Функция энтропии Эверетта – Хиршмана.[35][36]
Фон
Хотя феноменология сверхтекучих состояний гелия-4 и гелия-3 очень похожа, микроскопические детали переходов сильно различаются. Атомы гелия-4 являются бозонами, и их сверхтекучесть можно понять в терминах Статистика Бозе – Эйнштейна что они подчиняются. В частности, сверхтекучесть гелия-4 можно рассматривать как следствие конденсации Бозе – Эйнштейна во взаимодействующей системе. С другой стороны, атомы гелия-3 являются фермионами, и сверхтекучий переход в этой системе описывается обобщением теории Теория BCS сверхпроводимости. В этом, Купер спаривание происходит между атомами, а не электроны, а привлекательное взаимодействие между ними опосредуется вращение колебания, а не фононы. (Видеть фермионный конденсат.) Единое описание сверхпроводимости и сверхтекучести возможно в терминах нарушение калибровочной симметрии.
Сверхтекучие жидкости, такие как гелий-4 ниже лямбда-точки, проявляют много необычных свойств. (Видеть Гелий # Гелий II.) Сверхтекучая жидкость действует, как если бы она была смесью нормального компонента, обладающего всеми свойствами нормальной жидкости, и сверхтекучего компонента. Сверхтекучая составляющая имеет нулевую вязкость и нулевую энтропию. Приложение тепла к пятну в сверхтекучем гелии приводит к потоку нормального компонента, который обеспечивает перенос тепла с относительно высокой скоростью (до 20 см / с), что приводит к очень высокой эффективной теплопроводности.
Еще одно фундаментальное свойство становится видимым, если сверхтекучая жидкость помещается во вращающийся контейнер. Вместо того, чтобы равномерно вращаться вместе с контейнером, состояние вращения состоит из квантованных вихрей. То есть, когда контейнер вращается со скоростью ниже первой критической угловой скорости, жидкость остается совершенно неподвижной. При достижении первой критической угловой скорости сверхтекучая жидкость образует вихрь. Сила вихря квантуется, то есть сверхтекучая жидкость может вращаться только при определенных «разрешенных» значениях. Вращение в обычной жидкости, такой как вода, не квантуется. Если увеличить скорость вращения, будет образовываться все больше и больше квантованных вихрей, которые будут располагаться в красивых узорах, похожих на Решетка Абрикосова в сверхпроводнике.
Практическое применение
В последнее время в области химии сверхтекучий гелий-4 успешно применяется в спектроскопический методы как квантовый растворитель. Этот метод, называемый спектроскопией капель сверхтекучего гелия (SHeDS), представляет большой интерес для изучения молекул газа, поскольку отдельная молекула, сольватированная в сверхтекучей среде, позволяет молекуле иметь эффективную вращательную свободу, позволяя ей вести себя так же, как в сверхтекучей среде. «газовая» фаза. Капли сверхтекучего гелия также имеют характеристическую температуру около 0,4 К, которая охлаждает сольватированную молекулу (ы) до земли или почти измельченной. ровиброник государственный.
Сверхтекучие жидкости также используются в высокоточных устройствах, таких как гироскопы, которые позволяют измерять некоторые теоретически предсказанные гравитационные эффекты (например, см. Гравитационный зонд B ).
Инфракрасный астрономический спутник IRAS Запущенный в январе 1983 года для сбора данных в инфракрасном диапазоне был охлажден 73 килограммами сверхтекучего гелия, поддерживая температуру 1,6 К (-271,55 ° C). При использовании в сочетании с гелием-3 в экспериментах с экстремально низкими температурами обычно достигаются температуры до 40 мК. Гелий-3 в жидком состоянии при 3,2 К может испаряться в сверхтекучий гелий-4, где он действует как газ из-за свойств последнего как конденсата Бозе-Эйнштейна. Это испарение отбирает энергию из всей системы, которая может откачиваться способом, полностью аналогичным обычным методам охлаждения.
Технология сверхтекучего гелия используется для расширения температурного диапазона криокулеры к более низким температурам. Пока предел составляет 1,19 К, но есть потенциал для достижения 0,7 К.[37]
Развития 21 века
В начале 2000-х физики создали Фермионный конденсат из пар ультрахолодных фермионных атомов. При определенных условиях фермионные пары образуют двухатомные молекулы и пройти Конденсация Бозе – Эйнштейна. На другом пределе фермионы (особенно сверхпроводящие электроны) образуют Куперовские пары которые также обладают сверхтекучестью. Эта работа с ультрахолодными атомными газами позволила ученым изучить область между этими двумя крайностями, известную как Кроссовер BEC-BCS.
Сверхтвердые также могли быть открыты в 2004 году физиками на Государственный университет Пенсильвании. Когда гелий-4 охлаждается ниже примерно 200 мК под высоким давлением, часть (≈1%) твердого вещества, кажется, становится сверхтекучей.[38][39] Путем быстрого охлаждения или удлинения отжиг Время, таким образом увеличивая или уменьшая плотность дефектов, соответственно, с помощью эксперимента с торсионным осциллятором было показано, что доля сверхтвердого тела может составлять от 20% до полного отсутствия. Это говорит о том, что сверхтвердый характер гелия-4 присущ не гелию-4, а свойству гелия-4 и беспорядку.[40][41] Некоторые возникающие теории утверждают, что сверхтвердый сигнал, наблюдаемый в гелии-4, на самом деле был наблюдением либо сверхстекло государственный[42] или по сути сверхтекучие границы зерен в кристалле гелия-4.[43]
Смотрите также
Рекомендации
- ^ Капица, П. (1938). «Вязкость жидкого гелия ниже λ-точки». Природа. 141 (3558): 74. Bibcode:1938Натура.141 ... 74К. Дои:10.1038 / 141074a0. S2CID 3997900.
- ^ Allen, J. F .; Мизенер, А. Д. (1938). «Течение жидкого гелия II». Природа. 142 (3597): 643. Bibcode:1938Натура.142..643А. Дои:10.1038 / 142643a0. S2CID 4135906.
- ^ «Нобелевская премия по физике 1996 г. - Дополнительная информация». www.nobelprize.org. Получено 10 февраля, 2017.
- ^ Hall, H.E .; Винен, В. Ф. (1956). «Вращение жидкого гелия II. II. Теория взаимного трения в равномерно вращающемся гелии II». Труды Королевского общества A: математические, физические и инженерные науки. 238 (1213): 215. Bibcode:1956RSPSA.238..215H. Дои:10.1098 / rspa.1956.0215. S2CID 120738827.
- ^ Rayfield, G .; Рейф Ф. (1964). «Квантованные вихревые кольца в сверхтекучем гелии». Физический обзор. 136 (5A): A1194. Bibcode:1964ПхРв..136.1194Р. Дои:10.1103 / PhysRev.136.A1194.
- ^ Паккард, Ричард Э. (1982). «Вихревая фотография в жидком гелии» (PDF). Physica B. 109–110: 1474–1484. Bibcode:1982PhyBC.109.1474P. CiteSeerX 10.1.1.210.8701. Дои:10.1016/0378-4363(82)90510-1.
- ^ Avenel, O .; Вароко, Э. (1985). «Наблюдение одноквантованных событий рассеяния, подчиняющихся соотношению частот Джозефсона в критическом потоке сверхтекучей ^ {4} He через отверстие». Письма с физическими проверками. 55 (24): 2704–2707. Bibcode:1985ПхРвЛ..55.2704А. Дои:10.1103 / PhysRevLett.55.2704. PMID 10032216.[постоянная мертвая ссылка ]
- ^ Бьюли, Грегори П .; Lathrop, Daniel P .; Шринивасан, Катепалли Р. (2006). «Сверхтекучий гелий: Визуализация квантованных вихрей» (PDF). Природа. 441 (7093): 588. Bibcode:2006Натура.441..588Б. Дои:10.1038 / 441588a. PMID 16738652. S2CID 4429923.
- ^ Свенсон, К. (1950). «Преобразование жидкость-твердое тело в гелии вблизи абсолютного нуля». Физический обзор. 79 (4): 626. Bibcode:1950PhRv ... 79..626S. Дои:10.1103 / PhysRev.79.626.
- ^ Keesom, W.H .; Кеесом, А.П. (1935). «Новые измерения теплоемкости жидкого гелия». Physica. 2 (1): 557. Bibcode:1935Phy ..... 2..557K. Дои:10.1016 / S0031-8914 (35) 90128-8.
- ^ Buckingham, M.J .; Fairbank, W.M. (1961). «Глава III. Природа λ-перехода в жидком гелии». Природа λ-перехода в жидком гелии. Успехи физики низких температур. 3. п. 80. Дои:10.1016 / S0079-6417 (08) 60134-1. ISBN 978-0-444-53309-8.
- ^ E.L. Андроникашвили Ж. Эксп. Теор. Физ. Т. 16, с. 780 (1946), Т. 18, с. 424 (1948)
- ^ Охба, Томонори (2016). «Ограниченный квантовый перенос гелия через наноканалы за счет квантовых колебаний». Научные отчеты. 6: 28992. Bibcode:2016НатСР ... 628992O. Дои:10.1038 / srep28992. ЧВК 4929499. PMID 27363671.
- ^ С. Дж. Путтерман, Сверхтекучая гидродинамика (издательство North-Holland Publishing Company, Амстердам, 1974) ISBN 0-444-10681-2.
- ^ Л. Д. Ландау, J. Phys. СССР, Т. 5 (1941) с. 71.
- ^ Халатников И.М. Введение в теорию сверхтекучести (В.А.Benjamin, Inc., Нью-Йорк, 1965 г.) ISBN 0-7382-0300-9.
- ^ Van Alphen, W. M .; Van Haasteren, G.J .; De Bruyn Ouboter, R .; Таконис, К. В. (1966). «Зависимость критической скорости сверхтекучей жидкости от диаметра канала и толщины пленки». Письма по физике. 20 (5): 474. Bibcode:1966ФЛ .... 20..474В. Дои:10.1016/0031-9163(66)90958-9.
- ^ De Waele, A. Th. ЯВЛЯЮСЬ.; Куэртен, Дж. Г. М. (1992). "Глава 3: Термодинамика и гидродинамика 3Он-4Он Смеси ». Термодинамика и гидродинамика 3Он-4Он смешивает. Успехи физики низких температур. 13. п. 167. Дои:10.1016 / S0079-6417 (08) 60052-9. ISBN 978-0-444-89109-9.
- ^ Staas, F.A .; Северинс, А.П .; Ван дер Варден, H.C.M. (1975). «Холодильник разбавления с впрыском сверхтекучей жидкости». Письма о физике A. 53 (4): 327. Bibcode:1975ФЛА ... 53..327С. Дои:10.1016/0375-9601(75)90087-0.
- ^ Castelijns, C .; Kuerten, J .; De Waele, A .; Гийсман, Х. (1985). "3Он течет в разбавленном 3Он-4Он смешивается при температуре от 10 до 150 мК ». Физический обзор B. 32 (5): 2870–2886. Bibcode:1985ПхРвБ..32.2870С. Дои:10.1103 / PhysRevB.32.2870. PMID 9937394.
- ^ J.C.H. Zeegers Критические скорости и взаимное трение в 3Он-4Он смешивает при низких температурах ниже 100 мК ', диссертация, Приложение A, Технологический университет Эйндховена, 1991.
- ^ Алонсо, Дж. Л .; Арес, Ф .; Брун, Дж. Л. (5 октября 2018 г.). «Раскрытие критерия консистентности Ландау и значения взаимопроникновения в« двухжидкостной »модели». Европейский физический журнал B. 91 (10): 226. arXiv:1806.11034. Bibcode:2018EPJB ... 91..226A. Дои:10.1140 / epjb / e2018-90105-x. ISSN 1434-6028. S2CID 53464405.
- ^ Ф. Лондон (1938). «Λ-феномен жидкого гелия и бозе-эйнштейновское вырождение». Природа. 141 (3571): 643–644. Bibcode:1938Натура.141..643L. Дои:10.1038 / 141643a0. S2CID 4143290.
- ^ Л. Тиса (1938). «Явления переноса в гелии II». Природа. 141 (3577): 913. Bibcode:1938Натура.141..913Т. Дои:10.1038 / 141913a0. S2CID 4116542.
- ^ Л. Тиса (1947). «Теория жидкого гелия». Phys. Rev. 72 (9): 838–854. Bibcode:1947ПхРв ... 72..838Т. Дои:10.1103 / PhysRev.72.838.
- ^ Bijl, A; де Бур, Дж; Михельс, А (1941). «Свойства жидкого гелия II». Physica. 8 (7): 655–675. Bibcode:1941Phy ..... 8..655B. Дои:10.1016 / S0031-8914 (41) 90422-6.
- ^ Браун, Л. М., изд. (2000). Избранные статьи Ричарда Фейнмана с комментариями. Мировая научная серия по физике ХХ века. 27. World Scientific. ISBN 978-9810241315.Раздел IV (страницы 313–414) имеет дело с жидким гелием.
- ^ Р. П. Фейнман (1954). «Атомная теория двухжидкостной модели жидкого гелия» (PDF). Phys. Rev. 94 (2): 262. Bibcode:1954ПхРв ... 94..262Ф. Дои:10.1103 / PhysRev.94.262.
- ^ Р. П. Фейнман и М. Коэн (1956). «Энергетический спектр возбуждений в жидком гелии». (PDF). Phys. Rev. 102 (5): 1189–1204. Bibcode:1956ПхРв..102.1189Ф. Дои:10.1103 / PhysRev.102.1189.
- ^ Т. Д. Ли; К. Хуанг и К. Н. Ян (1957). «Собственные значения и собственные функции бозе-системы твердых сфер и ее низкотемпературные свойства». Phys. Rev. 106 (6): 1135–1145. Bibcode:1957ПхРв..106.1135Л. Дои:10.1103 / PhysRev.106.1135.
- ^ Л. Лю; Л. С. Лю и К. В. Вонг (1964). «Твердосферный подход к спектру возбуждения в жидком гелии II». Phys. Rev. 135 (5A): A1166 – A1172. Bibcode:1964ПхРв..135.1166Л. Дои:10.1103 / PhysRev.135.A1166.
- ^ Ивашин А.П., Полуэктов Ю.М. (2011). "Коротковолновые возбуждения в нелокальной модели Гросса-Питаевского". Cent. Евро. J. Phys. 9 (3): 857–864. arXiv:1004.0442. Bibcode:2010CEJPh.tmp..120I. Дои:10.2478 / с11534-010-0124-7. S2CID 118633189.
- ^ Злощастиев К.Г. (2012). «Объемно-элементная структура и ротон-максон-фононные возбуждения в сверхтекучем гелии вне приближения Гросса-Питаевского». Евро. Phys. J. B. 85 (8): 273. arXiv:1204.4652. Bibcode:2012EPJB ... 85..273Z. Дои:10.1140 / epjb / e2012-30344-3. S2CID 118545094.
- ^ Авдеенков А.В., Злощастиев К.Г. (2011). «Квантовые бозе-жидкости с логарифмической нелинейностью: самоподдерживаемость и возникновение пространственной протяженности». J. Phys. Летучая мышь. Мол. Опт. Phys. 44 (19): 195303. arXiv:1108.0847. Bibcode:2011JPhB ... 44s5303A. Дои:10.1088/0953-4075/44/19/195303. S2CID 119248001.
- ^ Хью Эверетт, III. Многомировая интерпретация квантовой механики: теория универсальной волновой функции. Диссертация Эверетта
- ^ И. Хиршман младший, Замечание об энтропии. Американский журнал математики (1957), стр. 152–156.
- ^ Танаева, И. А. (2004). «Сверхтекучий вихревой охладитель». Материалы конференции AIP. 710. п. 1906 г. Дои:10.1063/1.1774894.
- ^ Э. Ким и М. Х. В. Чан (2004). «Вероятное наблюдение сверхтвердой гелиевой фазы». Природа. 427 (6971): 225–227. Bibcode:2004Натура 427..225K. Дои:10.1038 / природа02220. PMID 14724632. S2CID 3112651.
- ^ Исследовательская группа Моисея Чана. "Сверхтвердый В архиве 2013-04-08 в Wayback Machine." Государственный университет Пенсильвании, 2004.
- ^ Софи, А; Риттнер C (2006). «Наблюдение классической вращательной инерции и неклассических сверхтвердых сигналов в твердом 4 He ниже 250 мК». Phys. Rev. Lett. 97 (16): 165301. arXiv:cond-mat / 0604528. Bibcode:2006ПхРвЛ..97п5301Р. Дои:10.1103 / PhysRevLett.97.165301. PMID 17155406. S2CID 45453420.
- ^ Софи, А; Риттнер C (2007). «Беспорядок и сверхтвердое состояние твердого 4 He». Phys. Rev. Lett. 98 (17): 175302. arXiv:cond-mat / 0702665. Bibcode:2007PhRvL..98q5302R. Дои:10.1103 / PhysRevLett.98.175302. S2CID 119469548.
- ^ Бонинсеньи, М; Прокофьева (2006). «Сверхстеклая фаза 4 He». Phys. Rev. Lett. 96 (13): 135301. arXiv:cond-mat / 0603003. Bibcode:2006PhRvL..96m5301W. Дои:10.1103 / PhysRevLett.96.135301. PMID 16711998. S2CID 41657202.
- ^ Поллет, L; Бонинсеньи М (2007). «Сверхтекучесть границ зерен в твердом 4 He». Phys. Rev. Lett. 98 (13): 135301. arXiv:cond-mat / 0702159. Bibcode:2007ПхРвЛ..98м5301П. Дои:10.1103 / PhysRevLett.98.135301. PMID 17501209. S2CID 20038102.
дальнейшее чтение
- Лондон, Ф. Сверхтекучие жидкости (Уайли, Нью-Йорк, 1950).
- D.R. Тилли, Дж. Тилли, `` Сверхтекучесть и сверхпроводимость. (IOP Publishing Ltd., Бристоль, 1990 г.)
- Хаген Кляйнерт, Калибровочные поля в конденсированных средах, Vol. I, "СУПЕРПОТОК И ВИХРЕВЫЕ ЛИНИИ", стр. 1–742, World Scientific (Сингапур, 1989 г.); Мягкая обложка ISBN 9971-5-0210-0 (также доступны онлайн )
- Энтони М. Гено: Основные сверхтекучие жидкости. Тейлор и Фрэнсис, Лондон, 2003 г., ISBN 0-7484-0891-6
- Джеймс Ф. Аннетт: Сверхпроводимость, сверхтекучие жидкости и конденсаты. Oxford Univ. Press, Oxford 2005, ISBN 978-0-19-850756-7
- Леггетт, А. (1999). "Сверхтекучесть". Обзоры современной физики. 71 (2): S318 – S323. Bibcode:1999RvMPS..71..318L. Дои:10.1103 / RevModPhys.71.S318.
- Филипп Лебрен и Лоран Тавиан: Технология сверхтекучего гелия
внешняя ссылка
- Руссо, В. Г. (2014). «Сверхтекучая плотность в непрерывных и дискретных пространствах: избегая заблуждений». Физический обзор B. 90 (13): 134503. arXiv:1403.5472. Bibcode:2014ПхРвБ..90м4503Р. Дои:10.1103 / PhysRevB.90.134503. S2CID 118518974.
- Жидкий гелий II, сверхтекучий: демонстрация перехода лямбда-точки / парадокса вязкости / двухжидкостная модель / эффект фонтана / ползущая пленка / второй звук.
- Видео, показывающее странное поведение сверхтекучего гелия
- Сверхтекучие фазы гелия
- https://web.archive.org/web/20060408121158/http://www.aip.org/pt/vol-54/iss-2/p31.html
- http://web.mit.edu/newsoffice/2005/matter.html
- сверхтекучая гидродинамика
- Индийская статья о сверхтекучих состояниях
- Интерактивные свойства гелия-4















