Томографическая реконструкция - Tomographic reconstruction

Томографическая реконструкция это разновидность многомерного обратная задача где задача состоит в том, чтобы получить оценку конкретной системы из конечного числа прогнозы. Математическая основа для создания томографических изображений была заложена Иоганн Радон. Ярким примером приложений является реконструкция из компьютерная томография (КТ), где поперечные сечения пациентов получают неинвазивным способом. Последние события показали Преобразование радона и его инверсия, используемая для задач, связанных с реалистичной вставкой объекта, необходимой для тестирования и оценки. компьютерная томография использовать в охрана аэропорта.^[1]

Эта статья в целом относится к методам реконструкции для всех видов томография, но некоторые термины и физические описания относятся непосредственно к реконструкция рентгеновской компьютерной томографии.

Представляем формулу

Рисунок 1: Геометрия параллельного пучка, используемая в томографии и томографической реконструкции. Каждая проекция, полученная в результате томографии под определенным углом, состоит из набора линейных интегралов через объект.

Полученный томографический снимок пластикового фантома черепа. Проецируемые рентгеновские лучи четко видны на этом срезе, полученном с помощью компьютерной томографии, в виде изображения. артефакты, из-за ограниченного количества срезов проекции по углам.

Проекция объекта, полученная в результате томографического измерения, под заданным углом. ${\displaystyle \theta }$, состоит из набора линейные интегралы (см. рис. 1). Набор из множества таких проекций под разными углами, организованных в 2D, называется синограммой (см. Рис. 3). В рентгеновской компьютерной томографии линейный интеграл представляет собой полное ослабление луча рентгеновские лучи поскольку он движется по прямой через объект. Как упоминалось выше, результирующее изображение представляет собой 2D (или 3D) модель коэффициент затухания. То есть мы хотим найти изображение ${\displaystyle \mu (x,y)}$. Самый простой и легкий способ визуализировать метод сканирования - это система параллельная проекция, как и в первых сканерах. Для этого обсуждения мы рассматриваем данные, которые должны быть собраны как серию параллельных лучей в позиции ${\displaystyle r}$, поперек проекции под углом ${\displaystyle \theta }$. Это повторяется для разных углов. Затухание происходит экспоненциально в ткани:

${\displaystyle I=I_{0}\exp \left({-\int \mu (x,y)\,ds}\right)}$

куда ${\displaystyle \mu (x,y)}$ - коэффициент ослабления как функция положения. Следовательно, обычно полное затухание ${\displaystyle p}$ луча в позиции ${\displaystyle r}$, на проекции под углом ${\displaystyle \theta }$, задается линейным интегралом:

${\displaystyle p_{\theta }(r)=\ln \left({\frac {I}{I_{0}}}\right)=-\int \mu (x,y)\,ds}$

Используя систему координат на рисунке 1, значение ${\displaystyle r}$ на который точка ${\displaystyle (x,y)}$ будет проецироваться под углом ${\displaystyle \theta }$ дан кем-то:

${\displaystyle x\cos \theta +y\sin \theta =r\ }$

Таким образом, приведенное выше уравнение можно переписать как

${\displaystyle p_{\theta }(r)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\delta (x\cos \theta +y\sin \theta -r)\,dx\,dy}$

куда ${\displaystyle f(x,y)}$ представляет ${\displaystyle \mu (x,y)}$ и ${\displaystyle \delta ()}$ это Дельта-функция Дирака. Эта функция известна как Преобразование радона (или же синограмма) 2D-объекта.

В Преобразование Фурье проекции можно записать как

${\displaystyle P_{\theta }(\omega )=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }f(x,y)\exp[-j\omega (x\cos \theta +y\sin \theta )]\,dx\,dy=F(\Omega _{1},\Omega _{2})}$ куда ${\displaystyle \Omega _{1}=\omega \cos \theta ,\Omega _{2}=\omega \sin \theta }$^[2]

${\displaystyle P_{\theta }(\omega )}$ представляет собой срез двумерного преобразования Фурье ${\displaystyle f(x,y)}$ под углом ${\displaystyle \theta }$. С использованием обратное преобразование Фурье, формула обратного преобразования Радона может быть легко выведена.

${\displaystyle f(x,y)={\frac {1}{2\pi }}\int \limits _{0}^{\pi }g_{\theta }(x\cos \theta +y\sin \theta )d\theta }$

куда ${\displaystyle g_{\theta }(x\cos \theta +y\sin \theta )}$ является производной от Преобразование Гильберта из ${\displaystyle p_{\theta }(r)}$

Теоретически обратное преобразование Радона даст исходное изображение. В теорема о проекции говорит нам, что если бы у нас было бесконечное количество одномерных проекций объекта, снятых под бесконечным числом углов, мы могли бы идеально восстановить исходный объект, ${\displaystyle f(x,y)}$. Однако на практике будет доступно лишь ограниченное число прогнозов.

Предполагая ${\displaystyle f(x,y)}$ имеет эффективный диаметр ${\displaystyle d}$ и желаемое разрешение ${\displaystyle R_{s}}$, количество проекций, необходимых для реконструкции, составляет ${\displaystyle N>\pi d/R_{s}}$^[2]

Алгоритмы реконструкции

Практичный алгоритмы реконструкции были разработаны для реализации процесса восстановления трехмерного объекта по его проекциям.^[3][2] Эти алгоритмы разработаны в основном на основе математики Преобразование радона, статистические знания о процессе сбора данных и геометрии системы визуализации данных.

Алгоритм восстановления Фурье-области

Реконструкция может быть произведена с помощью интерполяции. Предполагать ${\displaystyle N}$-проекции ${\displaystyle f(x,y)}$ генерируются под одинаковыми углами, каждый с одинаковой частотой дискретизации. В Дискретное преобразование Фурье на каждой проекции даст выборку в частотной области. Объединение всех проекций с частотной дискретизацией приведет к созданию полярного растра в частотной области. Полярный растр будет разреженным, поэтому для заполнения неизвестных точек ДПФ используется интерполяция, а реконструкция может быть выполнена с помощью обратное дискретное преобразование Фурье.^[4] Производительность реконструкции можно улучшить, разработав методы для изменения разреженности полярного растра, что повысит эффективность интерполяции.

Например, концентрический квадратный растр в частотной области можно получить, изменив угол между каждой проекцией следующим образом:

${\displaystyle \theta '={\frac {R_{0}}{\max\{|\cos \theta |,|\sin \theta |\}}}}$

куда ${\displaystyle R_{0}}$ самая высокая частота для оценки.

Концентрический квадратный растр повышает эффективность вычислений, позволяя размещать все позиции интерполяции на прямоугольной решетке ДПФ. Кроме того, это уменьшает ошибку интерполяции.^[4] Тем не менее, у алгоритма преобразования Фурье есть недостаток, заключающийся в том, что он создает на выходе изначально зашумленный результат.

Алгоритм обратной проекции

В практике восстановления томографических изображений часто стабилизированные и дискретизированный используется версия обратного преобразования Радона, известная как обратная проекция с фильтром алгоритм.^[2]

Для дискретной системы с дискретизацией обратное преобразование Радона имеет вид

${\displaystyle f(x,y)={\frac {1}{2\pi }}\sum _{i=0}^{N-1}\Delta \theta _{i}g_{\theta _{i}}(x\cos \theta _{i}+y\sin \theta _{i})}$

${\displaystyle g_{\theta }(t)=p_{\theta }(t)\cdot k(t)}$

куда ${\displaystyle \Delta \theta }$ угловое расстояние между выступами и ${\displaystyle k(t)}$ ядро радона с частотной характеристикой ${\displaystyle |\omega |}$.

Название «обратная проекция» происходит от того факта, что одномерная проекция должна быть отфильтрована одномерным ядром Радона (обратная проекция), чтобы получить двухмерный сигнал. Используемый фильтр не содержит усиления постоянного тока, поэтому добавляется Смещение постоянного тока может быть желательно. Реконструкция с использованием обратной проекции обеспечивает лучшее разрешение, чем метод интерполяции, описанный выше. Однако он вызывает больший шум, поскольку фильтр склонен усиливать высокочастотный контент.

Алгоритм итеративной реконструкции

Основная статья: Итерационная реконструкция

Итерационный алгоритм требует больших вычислительных ресурсов, но позволяет включать априори информация о системе ${\displaystyle f(x,y)}$.^[2]

Позволять ${\displaystyle N}$ быть количеством выступов, ${\displaystyle D_{i}}$ быть оператором искажения для ${\displaystyle i}$-я проекция сделана под углом ${\displaystyle \theta _{i}}$. ${\displaystyle \{\lambda _{i}\}}$ - это набор параметров для оптимизации преобразования итераций.

${\displaystyle f_{0}(x,y)=\sum _{i=1}^{N}\lambda _{i}p_{\theta _{i}}(r)}$

Веерная реконструкция Shepp-Logan Phantom с другим расстоянием между датчиками. Меньшее расстояние между датчиками позволяет более точно реконструировать. Рисунок был создан с использованием MATLAB.

${\displaystyle f_{k}(x,y)=f_{k-1}(x,y)+\sum _{i=1}^{N}\lambda _{i}[p_{\theta _{i}}(r)-D_{i}f_{k-1}(x,y)]}$

Альтернативным семейством рекурсивных алгоритмов томографической реконструкции являются Алгебраические методы реконструкции и итеративная разреженная асимптотическая минимальная дисперсия.

Реконструкция веерного луча

Использование неколлимированного веерного луча является обычным, поскольку коллимированный пучок излучения получить сложно. Веерные лучи будут генерировать серию линейных интегралов, не параллельных друг другу, в качестве проекций. Для системы веерного луча потребуется диапазон углов в 360 градусов, что налагает механические ограничения, однако она позволяет быстрее получать сигнал, что может быть выгодно в определенных условиях, например, в области медицины. Обратное проецирование следует аналогичной двухэтапной процедуре, которая приводит к реконструкции путем вычисления обратных проекций взвешенной суммы, полученных из отфильтрованных проекций.

Реконструкция глубокого обучения

Влияние пуассоновского шума на реконструкцию глубокого обучения, когда пуассоновский шум заставляет U-Net не восстанавливать существующий высококонтрастный объект, похожий на поражение.

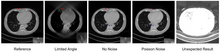
В настоящее время методы глубокого обучения широко применяются для реконструкции изображений и достигли впечатляющих результатов в различных задачах реконструкции изображений, включая шумоподавление с малой дозой, восстановление разреженного изображения, томографию с ограниченным углом и уменьшение металлических артефактов. Отличный обзор - в спецвыпуске ^[5] транзакции IEEE по медицинской визуализации. Одна группа алгоритмов реконструкции с глубоким обучением применяет нейронные сети постобработки для достижения реконструкции изображения в изображение, когда входные изображения восстанавливаются обычными методами реконструкции. Примером такого применения является уменьшение артефактов с помощью U-Net в томографии с ограниченным углом.^[6] Однако некорректные структуры могут появиться в изображении, восстановленном таким полностью управляемым данными методом,^[7] как показано на рисунке. Следовательно, интеграция известных операторов в архитектуру нейронных сетей оказывается полезной, как описано в концепции точного обучения.^[8] Например, прямая реконструкция изображения из данных проекции может быть изучена в рамках фильтрованной обратной проекции.^[9] Другой пример - построение нейронных сетей путем развертывания алгоритмов итеративной реконструкции.^[10] За исключением точного обучения, использование обычных методов реконструкции с реконструкцией глубокого обучения до ^[11] также является альтернативным подходом для улучшения качества изображения реконструкции глубокого обучения.

Программное обеспечение для томографической реконструкции

Для гибкой томографической реконструкции доступны наборы инструментов с открытым исходным кодом, такие как PYRO-NN,^[12] ТомоПы,^[13] КОНРАД,^[14] ODL, набор инструментов ASTRA,^[15][16] и ТИГРЭ.^[17] TomoPy - это набор инструментов Python с открытым исходным кодом для выполнения задач обработки томографических данных и реконструкции изображений на Расширенный источник фотонов в Аргоннская национальная лаборатория. Набор инструментов TomoPy специально разработан для простоты использования и развертывания на линии синхротронного оборудования. Он поддерживает чтение многих распространенных форматов данных синхротрона с диска посредством обмена научными данными,^[18] и включает несколько других алгоритмов обработки, обычно используемых для синхротронных данных. TomoPy также включает несколько алгоритмов реконструкции, которые можно запускать на многоядерных рабочих станциях и крупномасштабных вычислительных средствах.^[19] ASTRA Toolbox - это набор инструментов MATLAB и Python, состоящий из высокопроизводительных примитивов графического процессора для 2D и 3D томографии, с 2009 по 2014 год, разработанный iMinds-Vision Lab, Университет Антверпена и с 2014 года совместно разработанный iMinds-VisionLab (теперь imec-VisionLab) , UAntwerpen и CWI, Амстердам. Набор инструментов поддерживает параллельный, веерный и конический луч с очень гибким расположением источника / детектора. Большое количество алгоритмов реконструкции доступно через TomoPy и набор инструментов ASTRA, включая FBP, Gridrec, ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО, SIRT, SART, BART, CGLS, PML, MLEM и OSEM. Недавно набор инструментов ASTRA был интегрирован в структуру TomoPy.^[20] Благодаря интеграции набора инструментов ASTRA в структуру TomoPy, оптимизированные методы реконструкции на основе графического процессора становятся легко доступными для пользователей синхротронного луча, а пользователи набора инструментов ASTRA могут более легко читать данные и использовать другие функции TomoPy для фильтрации данных и исправления артефактов.

Галерея

В галерее показан полный процесс простой томографии объекта и последующей томографической реконструкции на основе ART.

• 

  Рис. 2: Фантом объект, две кошачьи уголки.

• 

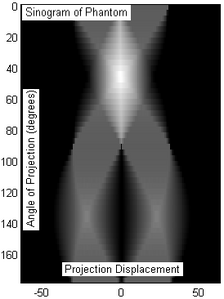
  Рис. 3: Синограмма фантомного объекта (Рис. 2), полученная по результатам томографии. 50 проекционных срезов были сделаны под углом 180 градусов, эквидистантно отобранных (только по совпадению смещение по оси x составляет -50/50 единиц).

• 

  Рис.4: ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО на основе томографической реконструкции синограммы на фиг.3, представленной в виде анимации в процессе итеративной реконструкции. Исходный объект можно приблизительно реконструировать, так как полученное изображение имеет некоторые визуальные артефакты.

Смотрите также

• Операция компьютерной томографии # Томографическая реконструкция
• Реконструкция конической балки
• Промышленное компьютерное сканирование
• Системы промышленной томографии

Рекомендации

1. Мегерби, Н., Брекон, Т.П., Флиттон, Г.Т., Мутон, А. (октябрь 2013 г.). «Создание металлических артефактов на основе преобразования радона в трехмерной проекции изображения угроз» (PDF). Proc. SPIE Оптика и фотоника для борьбы с терроризмом, борьбы с преступностью и защиты. 8901. ШПИОН. С. 1–7. Дои:10.1117/12.2028506. Получено 5 ноября 2013.
2. Даджен и Мерсеро (1984). Многомерная цифровая обработка сигналов. Прентис-Холл.
3. Герман, Г. Т., Основы компьютерной томографии: Реконструкция изображения по проекции, 2-е издание, Springer, 2009 г.
4. Р. Мерсеро, А. Оппенгейм (1974). «Цифровая реконструкция многомерных сигналов по их проекциям». Труды IEEE. 62 (10): 1319–1338. Дои:10.1109 / proc.1974.9625. HDL:1721.1/13788.
5. Ван, Ге и Е, Чон Чу и Мюллер, Клаус и Фесслер, Джеффри А. (2018). «Реконструкция изображений - это новый рубеж машинного обучения». IEEE Transactions по медицинской визуализации. 37 (6): 1289–1296. Дои:10.1109 / TMI.2018.2833635. PMID  29870359.
6. Гу, Джавук и Йе, Чон Чхоль (2017). Остаточное обучение в многомасштабной вейвлет-области для КТ-реконструкции с ограниченным углом. Полностью 3D. С. 443–447.
7. Хуанг Ю., Вюрфль Т., Брейнингер К., Лю Л., Лаурич Г., Майер А. (2018). Некоторые исследования устойчивости глубокого обучения в ограниченно-угловой томографии. MICCAI. Дои:10.1007/978-3-030-00928-1_17.
8. Майер, Андреас К. и Сибен, Кристофер и Стимпел, Бернхард и Вюрфль, Тобиас и Хоффманн, Матис и Шебеш, Франк и Фу, Вейлин и Милль, Леонид и Клинг, Лассе и Кристиансен, Силке (2019). «Обучение с использованием известных операторов снижает максимальные пределы ошибок». Природа Машинный интеллект. 1 (8): 373–380. Дои:10.1038 / с42256-019-0077-5. ЧВК  6690833. PMID  31406960.
9. Тобиас Вуэрфль и Матис Хоффманн, Винсент Кристлайн, Катарина Брейнингер и Исин Хуанг, Матиас Унберат и Андреас Майер (2018). «Компьютерная томография с глубоким обучением: изучение весов области проекции из области изображения в задачах с ограниченным углом». IEEE Transactions по медицинской визуализации. 37 (6): 1454–1463. Дои:10.1109 / TMI.2018.2833499. PMID  29870373.
10. Дж. Адлер и О. Октем (2018). «Выученная первично-дуальная реконструкция». IEEE Transactions по медицинской визуализации. 37 (6): 1322–1332. arXiv:1707.06474. Дои:10.1109 / TMI.2018.2799231. PMID  29870362.
11. Хуанг Ю., Прейс А., Лауритч Г., Манхарт М., Хуанг Х., Майер А. (2019). Уменьшение артефактов с согласованием данных для томографии под ограниченным углом с предварительным глубоким обучением. Машинное обучение для реконструкции медицинских изображений. arXiv:1908.06792. Дои:10.1007/978-3-030-33843-5_10.
12. Сибен, Кристофер; Мичен, Маркус; Стимпел, Бернхард; Зейтц, Стефан; Ploner, Стефан; Майер, Андреас (2019). «PYRO-NN: операторы реконструкции Python в нейронных сетях». Медицинская физика. 46 (11): 5110–5115. arXiv:1904.13342. Bibcode:2019arXiv190413342S. Дои:10.1002 / mp.13753. ЧВК  6899669. PMID  31389023.
13. Гурсой Д., Де Карло Ф., Сяо X и Якобсен С. (2014). «TomoPy: платформа для анализа данных синхротронной томографии». Журнал синхротронного излучения. 22 (5): 1188–1193. Bibcode:2014SPIE.9212E..0NG. Дои:10.1107 / S1600577514013939. ЧВК  4181643. PMID  25178011.
14. А. Майер, Х. Г. Хофманн, М. Бергер, П. Фишер, К. Швеммер, Х. Ву, К. Мюллер, Дж. Хорнеггер, Дж. Чой, К. Рисс, А. Кейл, А. Фархиг (2013). «CONRAD - программный фреймворк для визуализации конического луча в радиологии». Медицинская физика. 40 (11): 111914. Дои:10.1118/1.4824926. ЧВК  3820625. PMID  24320447.
15. Ван Аарл В., Паленстайн В. Дж., Де Бенхауэр Дж., Альтанцис Т., Балс С., Батенбург К. Дж. И Дж. Зейберс (октябрь 2015 г.). «ASTRA Toolbox: платформа для разработки передовых алгоритмов электронной томографии». Ультрамикроскопия. 157: 35–47. Дои:10.1016 / j.ultramic.2015.05.002. PMID  26057688.
16. В. Ван Аарл, В. Дж. Паленстейн, Дж. Кант, Э. Янссенс, Ф. Блейхродт, А. Добравольски, Дж. Де Бенхауэр, К. Дж. Батенбург и Дж. Зейберс (2016). «Быстрая и гибкая рентгеновская томография с использованием инструментария ASTRA». Оптика Экспресс. 24 (22): 35–47. Bibcode:2016OExpr..2425129V. Дои:10.1364 / OE.24.025129. PMID  27828452.
17. Выпущено Университетом Бата и ЦЕРН.
    Бигури, Андер; Досандж, Манджит; Хэнкок, Стивен; Сулеймани, Манучехр (8 сентября 2016 г.). «TIGRE: набор инструментов MATLAB-GPU для реконструкции изображений КЛКТ». Биомедицинская физика и инженерный экспресс. 2 (5): 055010. Дои:10.1088/2057-1976/2/5/055010. ISSN  2057-1976.
18. Де Карло Ф., Гурсой Д., Мароне Ф., Риверс М., Паркинсон Ю. Д., Хан Ф., Шварц Н., Вайн Д. Д., Фогт С., Глебер С. К., Нараянан С., Ньювилл М., Ланциротти Т., Сан Y, Хонг Ю. П., Якобсен К. (2014 г. ). «Обмен научными данными: схема для хранения исходных и проанализированных данных на основе HDF5». Журнал синхротронного излучения. 22 (6): 35–47. Дои:10.1107 / S160057751401604X. PMID  25343788.
19. Бисер Т., Гурсой Д., Кеттимуту Р., Де Карло Ф. и Фостер И. (2016). «Оптимизация рабочих процессов томографической реконструкции на географически распределенных ресурсах». Журнал синхротронного излучения. 23 (4): 997–1005. Дои:10.1107 / S1600577516007980. ЧВК  5315096. PMID  27359149.
20. Pelt DM, Gursoy D, Batenburg KJ, De Carlo F, Palenstijna WJ и Sijbers J (2016). «Интеграция TomoPy и инструментария ASTRA для расширенной обработки и реконструкции данных томографического синхротрона». Журнал синхротронного излучения. 23 (3): 842–849. Дои:10.1107 / S1600577516005658. ЧВК  5315009. PMID  27140167.

дальнейшее чтение

• Авинаш Как & Малкольм Слейни (1988), Принципы компьютерной томографической визуализации, IEEE Press, ISBN  0-87942-198-3.
• Бруянт, П. «Аналитические и итерационные алгоритмы реконструкции в ОФЭКТ» Журнал ядерной медицины 43 (10): 1343-1358, 2002

внешняя ссылка

• Slaney, A.C. Kak и Malcolm. «Принципы компьютерной томографической визуализации». Slaney.org. Получено 7 сентября 2018.
• Insight ToolKit; программное обеспечение томографической поддержки с открытым исходным кодом
• "TomoPy - документация TomoPy 1.1.3". Tomopy.readthedocs.org. Получено 7 сентября 2018.
• Набор инструментов ASTRA (All Scales Tomographic Reconstruction Antwerp); очень гибкое, быстрое и открытое программное обеспечение для компьютерной томографической реконструкции
• NiftyRec; комплексное программное обеспечение для томографической реконструкции с открытым исходным кодом; Matlab и Python с возможностью создания сценариев
• Инструмент томографической реконструкции и визуализации с открытым исходным кодом
• «ITS plc - Томография электрических процессов для промышленной визуализации». Itoms.com. Получено 7 сентября 2018.