Спираль Бурдейка – Кокстера - Boerdijk–Coxeter helix

Спирали Кокстера из правильных тетраэдров

Поворот против часовой и часовой стрелки

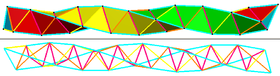Края могут быть окрашены в 6 групп, 3 основные спирали (голубой), с вогнутыми краями, образующими медленную прямую спираль (пурпурный), и две обратные спирали (желтая и оранжевая).

Спираль Бурдейка упаковка сфер имеет каждый сфера сосредоточен на вершина спирали Кокстера. Каждая сфера контактирует с 6 соседними сферами.

В Спираль Бурдейка – Кокстера, названный в честь Х. С. М. Коксетер и А. Х. Бурдейк, является линейной укладкой регулярных тетраэдры, расположенные так, что ребра комплекса, принадлежащие только одному тетраэдру, образуют три переплетенных спирали. Есть два хиральный формы с намоткой по часовой стрелке или против часовой стрелки. В отличие от любого другого набора Платоновы тела, спираль Бурдейка – Кокстера не имеет повторяющихся вращений в трехмерном пространстве. Даже в бесконечной цепочке сложенных друг над другом тетраэдров никакие два тетраэдра не будут иметь одинаковую ориентацию, потому что шаг спирали на ячейку не является рациональной долей окружности. Однако были обнаружены модифицированные формы этой спирали, которые имеют повторяющееся вращение,^[1] а в 4-мерном пространстве эта спираль повторяется в кольцах ровно из 30 тетраэдрических ячеек, которые составляют мозаику 3-сфера поверхность 600 ячеек, один из шести правильных выпуклых полихора.

Бакминстер Фуллер назвал это тетрахеликс и рассматривал их с правильными и неправильными тетраэдрическими элементами.^[2]

Геометрия

Координаты вершин спирали Бурдейка – Кокстера, составленной из тетраэдров с единичной длиной ребра, можно записать в виде

${\displaystyle (r\cos n\theta ,r\sin n\theta ,nh)}$

где ${\displaystyle r=3{\sqrt {3}}/10}$, ${\displaystyle \theta =\pm \cos ^{-1}(-2/3)}$, ${\displaystyle h=1/{\sqrt {10}}}$ и ${\displaystyle n}$ - произвольное целое число. Два разных значения ${\displaystyle \theta }$ соответствуют двум хиральным формам. Все вершины расположены на цилиндре радиуса ${\displaystyle r}$ по оси z. Есть еще один вписанный цилиндр с радиусом ${\displaystyle 3{\sqrt {2}}/20}$ внутри спирали.^[3]

Архитектура

В Art Tower Mito основан на спирали Бурдейка – Кокстера.

Многомерная геометрия

30 тетраэдрических колец из 600-ячеечной проекции

В 600 ячеек перегородки на 20 колец по 30 тетраэдры, каждый Спираль Бурдейка – Кокстера. При наложении на 3-сфера кривизна становится периодической, с периодом в десять вершин, охватывающим все 30 ячеек. Коллектив таких спиралей в 600-ячейке представляет собой дискретный Расслоение Хопфа. Если в трехмерном пространстве края представляют собой спирали, то в наложенной трехмерной сфере топология они есть геодезические и не иметь кручение. Они естественным образом закручиваются друг в друга из-за расслоения Хопфа. Коллектив ребер образует еще одно дискретное расслоение Хопфа из 12 колец с 10 вершинами в каждом. Они соответствуют кольцам из 10 додекаэдров в двойной 120-ячейке.

В дополнение 16 ячеек разбивается на два кольца 8-тетраэдров, длиной четыре ребра, и 5-элементный разбивает на одно вырожденное кольцо 5-тетраэдров.

4-многогранник	Кольца	Тетраэдры / кольцо	Продолжительность цикла	Сеть	Проекция
600 ячеек	20	30	30, 10^3, 15^2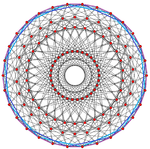
16 ячеек	2	8	8, 8, 4^2
5-элементный	1	5	(5, 5), 5

Связанные многогранные спирали

Равносторонний квадратные пирамиды также могут быть связаны в виде спирали с двумя конфигурации вершин, 3.4.3.4 и 3.3.4.3.3.4. Эта спираль существует как конечное кольцо 30 пирамид в 4-мерном многограннике.

И равносторонний пятиугольные пирамиды можно объединить в 3 конфигурации вершин: 3.3.5, 3.5.3.5 и 3.3.3.5.3.3.5:

Смотрите также

• Тороидальный многогранник
• Группа линий # Винтовая симметрия
• Косой апейрогон # Спиральные апейрогоны в 3-х измерениях

Примечания

1. Sadler et al. 2013.
2. Фуллер 1975, 930.00 Тетрахеликс.
3. «Данные Тетрахеликса».

Рекомендации

• Кокстер, Х. С. М. (1974). Регулярные сложные многогранники. Издательство Кембриджского университета. ISBN  052120125X.
• Boerdijk, A.H. (1952). «Несколько замечаний по поводу упаковки равных сфер». Philips Res. Представитель. 7: 303–313.
• Фуллер, Р. Бакминстер (1975). Applewhite, E.J. (ред.). Синергетика. Макмиллан.
• Пью, Энтони (1976). «5. Соединение многогранников §5.36 Тетрахеликс». Многогранники: визуальный подход. Калифорнийский университет Press. п. 53. ISBN  978-0-520-03056-5.
• Сэдлер, Гарретт; Клык, Клык; Ковач, Хулио; Клее, Ирвин (2013). «Периодическая модификация спирали Бордейка-Кокстера (тетрагеликс)». arXiv:1302.1174v1 [math.MG ].
• Лорд, E.A .; Ранганатан, С. (2004). «Структура γ-латуни и спираль Бурдейка – Кокстера» (PDF). Журнал некристаллических твердых тел. 334–335: 123–5. Bibcode:2004JNCS..334..121L. Дои:10.1016 / j.jnoncrysol.2003.11.069.
• Чжу, Ихань; Он, Jiating; Шан, Ченг; Мяо, Сяохэ; Хуанг, Цзяньфэн; Лю, Чжипань; Чен, Хунъюй; Хан, Ю (2014). «Хиральные золотые нанопроволоки со структурой Бурдейка – Кокстера – Бернала». Варенье. Chem. Soc. 136 (36): 12746–52. Дои:10.1021 / ja506554j. PMID  25126894.
• Лорд, Эрик А .; Mackay, Alan L .; Ранганатан, С. (2006). "§4.5 Спираль Бурдейка – Кокстера". Новая геометрия для новых материалов. Издательство Кембриджского университета. п. 64. ISBN  978-0-521-86104-5.
• Sadoc, J.F .; Ривье, Н. (1999). "Спираль Бурдейка-Кокстера и биологические спирали". Европейский физический журнал B. 12 (2): 309–318. Bibcode:1999EPJB ... 12..309S. Дои:10.1007 / с100510051009. S2CID  92684626.

внешняя ссылка

• Спиральная анимация Бурдейка-Кокстера
• http://www.rwgrayprojects.com/rbfnotes/helix/helix01.html