Теория пучка Эйлера – Бернулли - Euler–Bernoulli beam theory

Эта вибрирующая стеклянная балка может быть смоделирована как консольная балка с ускорением, переменной линейной плотностью, переменным модулем сечения, некоторого рода рассеянием, пружинящей концевой нагрузкой и, возможно, точечной массой на свободном конце.

Теория пучка Эйлера – Бернулли (также известен как теория пучка инженера или классическая теория пучка)^[1] это упрощение линейная теория упругости который позволяет рассчитать несущую и отклонение Характеристики балки. Он покрывает случай небольших отклонений луч которые подвергаются только боковым нагрузкам. Таким образом, это частный случай Теория пучка Тимошенко. Впервые он был провозглашен около 1750 г.^[2] но не применялась в больших масштабах до разработки Эйфелева башня и колесо обозрения в конце 19 века. После этих успешных демонстраций он быстро стал краеугольным камнем инженерной мысли и инструментом Вторая промышленная революция.

Дополнительный математические модели были разработаны такие как теория пластин, но простота теории пучков делает ее важным инструментом в науках, особенно структурный и машиностроение.

История

Схема поперечного сечения изогнутой балки с указанием нейтральной оси.

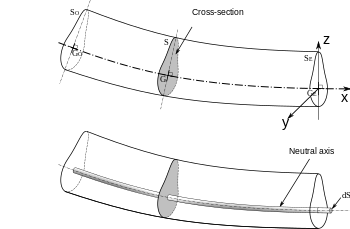
Преобладающий консенсус заключается в том, что Галилео Галилей сделали первые попытки разработать теорию пучков, но недавние исследования утверждают, что Леонардо да Винчи был первым, кто сделал важные наблюдения. Да Винчи не хватало Закон Гука и исчисление чтобы завершить теорию, тогда как Галилей сдерживался неверным предположением, которое он сделал.^[3]

Балка Бернулли названа в честь Джейкоб Бернулли, совершившие важные открытия. Леонард Эйлер и Даниэль Бернулли были первыми, кто сформулировал полезную теорию около 1750 года.^[4]В то время наука и инженерное дело обычно рассматривались как очень разные области, и существовали значительные сомнения в том, что математическому продукту академических кругов можно доверять для практических приложений безопасности. Мосты и здания продолжали проектироваться по прецеденту до конца 19 века, когда Эйфелева башня и колесо обозрения продемонстрировал справедливость теории в больших масштабах.

Уравнение статической балки

Уравнение Эйлера – Бернулли описывает соотношение между балками отклонение и приложенная нагрузка:^[5]

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,}$

Кривая ${\displaystyle w(x)}$ описывает прогиб балки в ${\displaystyle z}$ направление в некоторой позиции ${\displaystyle x}$ (напомним, что луч моделируется как одномерный объект). ${\displaystyle q}$ - распределенная нагрузка, другими словами сила на единицу длины (аналогично давление сила на площадь); это может быть функция ${\displaystyle x}$, ${\displaystyle w}$, или другие переменные. ${\displaystyle E}$ это модуль упругости и ${\displaystyle I}$ это второй момент площади поперечного сечения балки. ${\displaystyle I}$ должен быть рассчитан относительно оси, которая проходит через центр тяжести поперечного сечения и перпендикулярна приложенной нагрузке.^{[N 1]} Явно для балки, ось которой ориентирована вдоль Икс с погрузкой вместе z, поперечное сечение балки находится в yz плоскости, а соответствующий второй момент площади равен

${\displaystyle I=\iint z^{2}\;dy\;dz,}$

где предполагается, что центр тяжести поперечного сечения находится в точке у = z = 0.

Часто продукт ${\displaystyle EI}$ (известный как жесткость на изгиб ) - константа, так что

${\displaystyle EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=q(x).\,}$

Это уравнение, описывающее прогиб однородной статической балки, широко используется в инженерной практике. Табличные выражения для прогиба ${\displaystyle w}$ общие конфигурации балок можно найти в технических руководствах. Для более сложных ситуаций прогиб может быть определен путем решения уравнения Эйлера – Бернулли с использованием таких методов, как "прямая интеграция ", "Метод Маколея ", "метод моментной площади, "метод сопряженных пучков ", "принцип виртуальной работы ", "Метод Кастильяно ", "метод гибкости ", "метод отклонения откоса ", "метод распределения моментов ", или же "метод прямой жесткости ".

Здесь определены условные обозначения, поскольку в литературе можно найти различные условные обозначения.^[5] В этой статье правша система координат используется, как показано на рисунке Изгиб балки Эйлера – Бернулли. . С ${\displaystyle \mathbf {e_{z}} \times \mathbf {e_{x}} =\mathbf {e_{y}} }$ куда ${\displaystyle \mathbf {e_{x}} }$, ${\displaystyle \mathbf {e_{y}} }$, и ${\displaystyle \mathbf {e_{z}} }$ - единичные векторы в направлении осей x, y и z соответственно, направление оси y - на рисунке. Силы, действующие положительно ${\displaystyle x}$ и ${\displaystyle z}$ направления считаются положительными. Знак изгибающего момента ${\displaystyle M}$ является положительным, когда вектор крутящего момента, связанный с изгибающим моментом на правой стороне секции, находится в положительном направлении y (т. е. так, что положительное значение ${\displaystyle M}$ приводит к сжимающему напряжению в нижних волокнах). При таком выборе соглашения о знаках изгибающего момента, чтобы иметь ${\displaystyle dM=Qdx}$, необходимо, чтобы поперечная сила ${\displaystyle Q}$ действующий с правой стороны сечения должен быть положительным в направлении z, чтобы достичь статического равновесия моментов. Чтобы иметь силовое равновесие с ${\displaystyle dQ=qdx}$, интенсивность нагрузки ${\displaystyle q}$ должен быть положительным в отрицательном направлении z. В дополнение к этим соглашениям о знаках для скалярных величин мы также иногда используем векторы, в которых направления векторов проясняются с помощью единичных векторов, ${\displaystyle \mathbf {e_{x}} }$, ${\displaystyle \mathbf {e_{y}} }$, и ${\displaystyle \mathbf {e_{z}} }$.

Последовательные производные прогиба ${\displaystyle w}$ имеют важные физические значения: ${\displaystyle dw/dx}$ наклон балки,

${\displaystyle M=-EI{\frac {d^{2}w}{dx^{2}}}}$

это изгибающий момент в луче, и

${\displaystyle Q=-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}$

это сдвигающая сила в луче.

Изгиб балки Эйлера – Бернулли. Каждое поперечное сечение балки находится под углом 90 градусов к нейтральной оси.

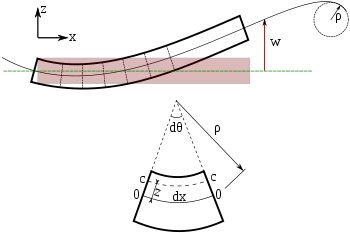
Напряжения в балке можно рассчитать из приведенных выше выражений после того, как будет определен прогиб из-за данной нагрузки.

Вывод уравнения изгиба

Ввиду фундаментальной важности уравнения изгибающего момента в технике мы сделаем краткий вывод. Переходим на полярные координаты. Длина нейтральной оси на рисунке равна ${\displaystyle \rho d\theta .}$ Длина волокна с радиальным расстоянием ${\displaystyle z}$ ниже нейтральной оси находится ${\displaystyle (\rho +z)d\theta .}$ Следовательно, деформация этого волокна равна

${\displaystyle {\frac {\left(\rho +z-\rho \right)\ d\theta }{\rho \ d\theta }}={\frac {z}{\rho }}.}$

Напряжение этого волокна составляет ${\displaystyle E{\tfrac {z}{\rho }}}$ куда ${\displaystyle E}$ это модуль упругости в соответствии с Закон Гука. Вектор дифференциальной силы, ${\displaystyle d\mathbf {F} ,}$ в результате этого напряжения определяется выражением

${\displaystyle d\mathbf {F} =E{\frac {z}{\rho }}dA\mathbf {e_{x}} .}$

Это вектор дифференциальной силы, действующей в правой части сечения, показанного на рисунке. Мы знаем, что это в ${\displaystyle \mathbf {e_{x}} }$ направление, поскольку на рисунке ясно видно, что волокна в нижней половине находятся в напряжении. ${\displaystyle dA}$ - дифференциальный элемент площади в месте расположения волокна. Вектор дифференциального изгибающего момента, ${\displaystyle d\mathbf {M} }$ связана с ${\displaystyle d\mathbf {F} }$ дан кем-то

${\displaystyle d\mathbf {M} =-z\mathbf {e_{z}} \times d\mathbf {F} =-\mathbf {e_{y}} E{\frac {z^{2}}{\rho }}dA.}$

Это выражение справедливо для волокон в нижней половине пучка. Выражение для волокон в верхней половине балки будет аналогичным, за исключением того, что вектор плеча момента будет в положительном направлении z, а вектор силы будет в направлении -x, поскольку верхние волокна находятся в состоянии сжатия. Но результирующий вектор изгибающего момента все равно будет в направлении -y, поскольку ${\displaystyle \mathbf {e_{z}} \times -\mathbf {e_{x}} =-\mathbf {e_{y}} .}$ Поэтому проинтегрируем по всему сечению балки и получим ${\displaystyle \mathbf {M} }$ вектор изгибающего момента, действующий на правое поперечное сечение балки, выражение

${\displaystyle \mathbf {M} =\int d\mathbf {M} =-\mathbf {e_{y}} {\frac {E}{\rho }}\int {z^{2}}\ dA=-\mathbf {e_{y}} {\frac {EI}{\rho }},}$

куда ${\displaystyle I}$ это второй момент площади. Из расчетов мы знаем, что когда ${\displaystyle {\tfrac {dw}{dx}}}$ мала, как и для пучка Эйлера – Бернулли, ${\displaystyle {\tfrac {1}{\rho }}={\tfrac {d^{2}w}{dx^{2}}}}$ (${\displaystyle \rho }$ это радиус кривизны ). Следовательно,

${\displaystyle \mathbf {M} =-\mathbf {e_{y}} EI{d^{2}w \over dx^{2}}.}$

Это векторное уравнение можно разделить в определении вектора единичного изгиба (M ориентирован как ey) и в уравнении изгиба:

${\displaystyle M=-EI{d^{2}w \over dx^{2}}.}$

Уравнение динамической балки

Метод конечных элементов модель колебаний широкополочной балки (я-луч ).

Уравнение динамической балки - это Уравнение Эйлера – Лагранжа. для следующего действия

${\displaystyle S=\int _{t_{1}}^{t_{2}}\int _{0}^{L}\left[{\frac {1}{2}}\mu \left({\frac {\partial w}{\partial t}}\right)^{2}-{\frac {1}{2}}EI\left({\frac {\partial ^{2}w}{\partial x^{2}}}\right)^{2}+q(x)w(x,t)\right]dxdt.}$

Первый член представляет собой кинетическую энергию, где ${\displaystyle \mu }$ - масса на единицу длины; второй представляет потенциальную энергию из-за внутренних сил (если рассматривать с отрицательным знаком), а третий член представляет потенциальную энергию из-за внешней нагрузки ${\displaystyle q(x)}$. В Уравнение Эйлера – Лагранжа. используется для определения функции, минимизирующей функционал ${\displaystyle S}$. Для динамической балки Эйлера – Бернулли уравнение Эйлера – Лагранжа имеет вид

${\displaystyle {\cfrac {\partial ^{2}}{\partial x^{2}}}\left(EI{\cfrac {\partial ^{2}w}{\partial x^{2}}}\right)=-\mu {\cfrac {\partial ^{2}w}{\partial t^{2}}}+q(x)}$

Вывод уравнения Эйлера – Лагранжа для балок.

Поскольку Лагранжиан является ${\displaystyle {\mathcal {L}}:={\tfrac {1}{2}}\mu \left({\frac {\partial w}{\partial t}}\right)^{2}-{\tfrac {1}{2}}EI\left({\frac {\partial ^{2}w}{\partial x^{2}}}\right)^{2}+q(x)w(x,t)={\tfrac {\mu }{2}}{\dot {w}}^{2}-{\tfrac {EI}{2}}w_{xx}^{2}+qw\equiv {\mathcal {L}}(x,t,w,{\dot {w}},w_{xx})}$ соответствующий Уравнение Эйлера – Лагранжа. является ${\displaystyle {\cfrac {\partial {\mathcal {L}}}{\partial w}}-{\frac {\partial }{\partial t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {w}}}}\right)+{\frac {\partial ^{2}}{\partial x^{2}}}\left({\frac {\partial {\mathcal {L}}}{\partial w_{xx}}}\right)=0}$ Сейчас же, ${\displaystyle {\cfrac {\partial {\mathcal {L}}}{\partial w}}=q~;~~{\frac {\partial {\mathcal {L}}}{\partial {\dot {w}}}}=\mu {\dot {w}}~;~~{\frac {\partial {\mathcal {L}}}{\partial w_{xx}}}=-EIw_{xx}~.}$ Подстановка в уравнение Эйлера – Лагранжа дает ${\displaystyle q-\mu {\ddot {w}}-(EIw_{xx})_{xx}=0}$ или же, ${\displaystyle {\cfrac {\partial ^{2}}{\partial x^{2}}}\left(EI{\cfrac {\partial ^{2}w}{\partial x^{2}}}\right)=-\mu {\cfrac {\partial ^{2}w}{\partial t^{2}}}+q}$ которое является основным уравнением динамики балки Эйлера – Бернулли.

Когда луч однороден, ${\displaystyle E}$ и ${\displaystyle I}$ не зависят от ${\displaystyle x}$, а уравнение пучка проще:

${\displaystyle EI{\cfrac {\partial ^{4}w}{\partial x^{4}}}=-\mu {\cfrac {\partial ^{2}w}{\partial t^{2}}}+q\,.}$

Бесплатная вибрация

При отсутствии поперечной нагрузки ${\displaystyle q}$, у нас есть свободная вибрация уравнение. Это уравнение можно решить с помощью разложения Фурье смещения на сумму гармонических колебаний вида

${\displaystyle w(x,t)={\text{Re}}[{\hat {w}}(x)~e^{-i\omega t}]}$

куда ${\displaystyle \omega }$ частота вибрации. Тогда для каждого значения частоты можно решить обыкновенное дифференциальное уравнение

${\displaystyle EI~{\cfrac {\mathrm {d} ^{4}{\hat {w}}}{\mathrm {d} x^{4}}}-\mu \omega ^{2}{\hat {w}}=0\,.}$

Общее решение вышеуказанного уравнения:

${\displaystyle {\hat {w}}=A_{1}\cosh(\beta x)+A_{2}\sinh(\beta x)+A_{3}\cos(\beta x)+A_{4}\sin(\beta x)\quad {\text{with}}\quad \beta :=\left({\frac {\mu \omega ^{2}}{EI}}\right)^{1/4}}$

куда ${\displaystyle A_{1},A_{2},A_{3},A_{4}}$ являются константами. Эти константы уникальны для данного набора граничных условий. Однако решение для смещения не однозначно и зависит от частоты. Эти решения обычно записываются как

${\displaystyle {\hat {w}}_{n}=A_{1}\cosh(\beta _{n}x)+A_{2}\sinh(\beta _{n}x)+A_{3}\cos(\beta _{n}x)+A_{4}\sin(\beta _{n}x)\quad {\text{with}}\quad \beta _{n}:=\left({\frac {\mu \omega _{n}^{2}}{EI}}\right)^{1/4}\,.}$

Количество ${\displaystyle \omega _{n}}$ называются собственные частоты балки. Каждое из решений смещения называется Режим а форма кривой смещения называется форма моды.

Пример: консольная балка

Формы мод для первых четырех мод вибрирующей консольной балки.

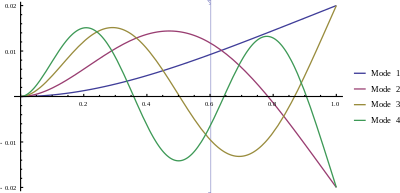
Граничные условия для консольной балки длины ${\displaystyle L}$ (исправлено на ${\displaystyle x=0}$) находятся

${\displaystyle {\begin{aligned}&{\hat {w}}_{n}=0~,~~{\frac {d{\hat {w}}_{n}}{dx}}=0\quad {\text{at}}~~x=0\\&{\frac {d^{2}{\hat {w}}_{n}}{dx^{2}}}=0~,~~{\frac {d^{3}{\hat {w}}_{n}}{dx^{3}}}=0\quad {\text{at}}~~x=L\,.\end{aligned}}}$

При применении этих условий обнаруживается, что нетривиальные решения существуют, только если${\displaystyle \cosh(\beta _{n}L)\,\cos(\beta _{n}L)+1=0\,.}$Это нелинейное уравнение можно решить численно. Первые несколько корней β₁ L / π = 0.59686..., β₂ L / π = 1.49418..., β₃ L / π = 2.50025..., β₄ L / π = 3.49999..., ...

Соответствующие собственные частоты колебаний равны

${\displaystyle \omega _{1}=\beta _{1}^{2}{\sqrt {\frac {EI}{\mu }}}={\frac {3.5161}{L^{2}}}{\sqrt {\frac {EI}{\mu }}}~,~~\dots }$

Граничные условия также могут использоваться для определения форм колебаний из решения для смещения:

${\displaystyle {\hat {w}}_{n}=A_{1}{\Bigl [}(\cosh \beta _{n}x-\cos \beta _{n}x)+{\frac {\cos \beta _{n}L+\cosh \beta _{n}L}{\sin \beta _{n}L+\sinh \beta _{n}L}}(\sin \beta _{n}x-\sinh \beta _{n}x){\Bigr ]}}$

Неизвестная константа (на самом деле константа, так как для каждого ${\displaystyle n}$), ${\displaystyle A_{1}}$, которая в целом является сложной, определяется начальными условиями при ${\displaystyle t=0}$ от скорости и перемещений балки. Обычно значение ${\displaystyle A_{1}=1}$ используется при построении форм колебаний. Решения проблемы принудительной нагрузки без демпфирования имеют неограниченные смещения, когда частота возбуждения совпадает с собственной частотой ${\displaystyle \omega _{n}}$, т.е. пучок может резонировать. Таким образом, собственные частоты балки соответствуют частотам, на которых резонанс может случиться.

Пример: безопорная (свободная) балка

Первые четыре режима колеблющейся свободно-свободной балки Эйлера-Бернулли.

Свободная балка - это балка без опор.^[6] Граничные условия для свободной балки длины L от Икс= От 0 до Икс= L определяется как:

${\displaystyle {\frac {d^{2}{\hat {w}}_{n}}{dx^{2}}}=0~,~~{\frac {d^{3}{\hat {w}}_{n}}{dx^{3}}}=0\quad {\text{at}}~~x=0\,{\text{and}}\,L\,.}$

Если мы применяем эти условия, обнаруживается, что нетривиальные решения существуют, только если${\displaystyle \cosh(\beta _{n}L)\,\cos(\beta _{n}L)-1=0\,.}$

Это нелинейное уравнение можно решить численно. Первые несколько корней β₁ L / π = 1.50562..., β₂ L / π = 2.49975..., β₃ L / π = 3.50001..., β₄ L / π = 4.50000...

Соответствующие собственные частоты колебаний:

${\displaystyle \omega _{1}=\beta _{1}^{2}{\sqrt {\frac {EI}{\mu }}}={\frac {22.3733}{L^{2}}}{\sqrt {\frac {EI}{\mu }}}~,~~\dots }$

Граничные условия также могут использоваться для определения форм колебаний из решения для смещения:

${\displaystyle {\hat {w}}_{n}=A_{1}{\Bigl [}(\cos \beta _{n}x+\cosh \beta _{n}x)-{\frac {\cos \beta _{n}L-\cosh \beta _{n}L}{\sin \beta _{n}L-\sinh \beta _{n}L}}(\sin \beta _{n}x+\sinh \beta _{n}x){\Bigr ]}}$

Как и в случае с консольной балкой, неизвестные константы определяются начальными условиями при ${\displaystyle t=0}$ от скорости и перемещений балки. Кроме того, решения проблемы принудительной нагрузки без демпфирования имеют неограниченные смещения, когда частота возбуждения соответствует собственной частоте. ${\displaystyle \omega _{n}}$.

Стресс

Помимо отклонения, уравнение балки описывает силы и моменты и поэтому может использоваться для описания подчеркивает. По этой причине уравнение Эйлера – Бернулли широко используется в инженерное дело, особенно гражданского и механического, для определения прочности (а также прогиба) балок при изгибе.

Оба изгибающий момент и сдвигающая сила вызвать напряжения в балке. Напряжение из-за поперечной силы максимально вдоль нейтральная ось балки (когда ширина балки t постоянна вдоль поперечного сечения балки; в противном случае необходимо вычислить интеграл, включающий первый момент и ширину балки для конкретного поперечного сечения), и максимальное растягивающее напряжение находится либо на верхней, либо на нижней поверхности. Таким образом, максимум основное напряжение в луче может быть не на поверхности и не в центре, а в некоторой общей области.Однако напряжения сдвига пренебрежимо малы по сравнению с напряжениями изгибающего момента во всех балках, кроме самых коренастых, а также тем фактом, что концентрации напряжений обычно возникают на поверхностях, а это означает, что максимальное напряжение в балке, вероятно, будет на поверхности.

Простая или симметричная гибка

Элемент изогнутой балки: волокна образуют концентрические дуги, верхние волокна сжаты, а нижние - растянуты.

Для поперечных сечений балки, симметричных относительно плоскости, перпендикулярной нейтральной плоскости, можно показать, что растягивающее напряжение, испытываемое балкой, может быть выражено как:

${\displaystyle \sigma ={\frac {Mz}{I}}=-zE~{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}.\,}$

Вот, ${\displaystyle z}$ - расстояние от нейтральной оси до интересующей точки; и ${\displaystyle M}$ изгибающий момент. Обратите внимание, что из этого уравнения следует, что чистый изгиб (с положительным знаком) вызовет нулевое напряжение на нейтральной оси, положительное (растягивающее) напряжение «вверху» балки и отрицательное (сжимающее) напряжение внизу балки; а также подразумевает, что максимальное напряжение будет на верхней поверхности, а минимальное - на нижней. Это напряжение изгиба может быть наложено на приложенные в осевом направлении напряжения, что вызовет смещение нейтральной (нулевое напряжение) оси.

Максимальные напряжения в поперечном сечении

Величины, используемые при определении модуля сечения балки.

Максимальное растягивающее напряжение в поперечном сечении находится в месте ${\displaystyle z=c_{1}}$ а максимальное сжимающее напряжение находится в точке ${\displaystyle z=-c_{2}}$ где высота поперечного сечения равна ${\displaystyle h=c_{1}+c_{2}}$. Эти стрессы

${\displaystyle \sigma _{1}={\cfrac {Mc_{1}}{I}}={\cfrac {M}{S_{1}}}~;~~\sigma _{2}=-{\cfrac {Mc_{2}}{I}}=-{\cfrac {M}{S_{2}}}}$

Количество ${\displaystyle S_{1},S_{2}}$ являются модули сечения^[5] и определяются как

${\displaystyle S_{1}={\cfrac {I}{c_{1}}}~;~~S_{2}={\cfrac {I}{c_{2}}}}$

Модуль сечения объединяет всю важную геометрическую информацию о сечении балки в одну величину. Для случая, когда балка дважды симметрична, ${\displaystyle c_{1}=c_{2}}$ и у нас есть один модуль сечения ${\displaystyle S=I/c}$.

Деформация в балке Эйлера – Бернулли.

Нам нужно выражение для напряжение в терминах прогиба нейтральной поверхности, чтобы связать напряжения в балке Эйлера-Бернулли с прогибом. Чтобы получить это выражение, мы используем предположение, что нормали к нейтральной поверхности остаются нормальными во время деформации и что прогибы малы. Эти предположения подразумевают, что балка изгибается по дуге окружности радиуса ${\displaystyle \rho }$ (см. рисунок 1) и что нейтральная поверхность не изменяется по длине во время деформации.^[5]

Позволять ${\displaystyle \mathrm {d} x}$ - длина элемента нейтральной поверхности в недеформированном состоянии. При небольших прогибах элемент не меняет свою длину после изгиба, а деформируется в дугу окружности радиуса. ${\displaystyle \rho }$. Если ${\displaystyle \mathrm {d} \theta }$ - угол, образуемый этой дугой, то ${\displaystyle \mathrm {d} x=\rho ~\mathrm {d} \theta }$.

Рассмотрим теперь еще один отрезок элемента на расстоянии ${\displaystyle z}$ над нейтральной поверхностью. Начальная длина этого элемента ${\displaystyle \mathrm {d} x}$. Однако после гибки длина элемента становится равной ${\displaystyle \mathrm {d} x'=(\rho -z)~\mathrm {d} \theta =\mathrm {d} x-z~\mathrm {d} \theta }$. Деформация в этом сегменте балки определяется выражением

${\displaystyle \varepsilon _{x}={\cfrac {\mathrm {d} x'-\mathrm {d} x}{\mathrm {d} x}}=-{\cfrac {z}{\rho }}=-\kappa ~z}$

куда ${\displaystyle \kappa }$ это кривизна балки. Это дает нам осевую деформацию в балке как функцию расстояния от нейтральной поверхности. Однако нам еще нужно найти связь между радиусом кривизны и прогибом балки. ${\displaystyle w}$.

Связь между кривизной и прогибом балки

Пусть P - точка на нейтральной поверхности балки на расстоянии ${\displaystyle x}$ от происхождения ${\displaystyle (x,z)}$ система координат. Наклон луча примерно равен углу нейтральной поверхности с ${\displaystyle x}$-ось для малых углов, встречающихся в теории пучка. Следовательно, в этом приближении

${\displaystyle \theta (x)={\cfrac {\mathrm {d} w}{\mathrm {d} x}}}$

Следовательно, для бесконечно малого элемента ${\displaystyle \mathrm {d} x}$, Соотношение ${\displaystyle \mathrm {d} x=\rho ~\mathrm {d} \theta }$ можно записать как

${\displaystyle {\cfrac {1}{\rho }}={\cfrac {\mathrm {d} \theta }{\mathrm {d} x}}={\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}=\kappa }$

Следовательно, деформация балки может быть выражена как

${\displaystyle \varepsilon _{x}=-z\kappa }$

Отношения напряжения и напряжения

Для однородного изотропный линейная эластичность материала, напряжение связано с деформацией ${\displaystyle \sigma =E\varepsilon }$, куда ${\displaystyle E}$ это Модуль для младших. Следовательно, напряжение в балке Эйлера – Бернулли определяется выражением

${\displaystyle \sigma _{x}=-zE{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}$

Обратите внимание, что указанное выше соотношение по сравнению с соотношением между осевым напряжением и изгибающим моментом приводит к

${\displaystyle M=-EI{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}$

Поскольку поперечная сила определяется выражением ${\displaystyle Q=\mathrm {d} M/\mathrm {d} x}$, у нас также есть

${\displaystyle Q=-EI{\cfrac {\mathrm {d} ^{3}w}{\mathrm {d} x^{3}}}}$

Граничные соображения

Уравнение пучка содержит производную четвертого порядка по ${\displaystyle x}$. Найти уникальное решение ${\displaystyle w(x,t)}$ нам нужно четыре граничных условия. Граничные условия обычно моделируют поддерживает, но они также могут моделировать точечные нагрузки, распределенные нагрузки и моменты. В поддержка или граничные условия смещения используются для фиксации значений смещения (${\displaystyle w}$) и вращения (${\displaystyle \mathrm {d} w/\mathrm {d} x}$) на границе. Такие граничные условия также называют Граничные условия Дирихле. Граничные условия нагрузки и момента включают высшие производные от ${\displaystyle w}$ и представляют поток импульса. Граничные условия потока также называют Граничные условия Неймана.

В качестве примера рассмотрим консоль балка, встроенная с одного конца и свободная с другого, как показано на рисунке рядом. На встроенном конце балки не может быть смещения или поворота балки. Это означает, что на левом конце отклонение и наклон равны нулю. Поскольку к свободному концу балки не прилагается внешний изгибающий момент, изгибающий момент в этом месте равен нулю. Кроме того, если к балке не приложена внешняя сила, поперечная сила на свободном конце также равна нулю.

Принимая ${\displaystyle x}$ координата левого конца как ${\displaystyle 0}$ и правый конец как ${\displaystyle L}$ (длина балки), эти утверждения переводятся в следующий набор граничных условий (предположим, что ${\displaystyle EI}$ постоянная):

${\displaystyle w|_{x=0}=0\quad ;\quad {\frac {\partial w}{\partial x}}{\bigg |}_{x=0}=0\qquad {\mbox{(fixed end)}}\,}$

Консольная балка.

${\displaystyle {\frac {\partial ^{2}w}{\partial x^{2}}}{\bigg |}_{x=L}=0\quad ;\quad {\frac {\partial ^{3}w}{\partial x^{3}}}{\bigg |}_{x=L}=0\qquad {\mbox{(free end)}}\,}$

Простая опора (штифт или ролик) эквивалентна силе точки на балке, которая регулируется таким образом, чтобы зафиксировать положение балки в этой точке. Фиксированная опора или зажим эквивалентны комбинации силы в точке и крутящего момента, который регулируется таким образом, чтобы зафиксировать как положение, так и наклон балки в этой точке. Точечные силы и крутящие моменты, исходящие от опор или непосредственно приложенные, разделят балку на набор сегментов, между которыми уравнение балки даст непрерывное решение с учетом четырех граничных условий, по два на каждом конце сегмента. Предполагая, что продукт EI является константой, и определяя ${\displaystyle \lambda =F/EI}$ куда F - величина точечной силы, а ${\displaystyle \tau =M/EI}$ куда M - величина точечного крутящего момента, граничные условия, подходящие для некоторых общих случаев, приведены в таблице ниже. Изменение конкретной производной от ш через границу как Икс увеличение обозначается ${\displaystyle \Delta }$ с последующим производным. Например, ${\displaystyle \Delta w''=w''(x+)-w''(x-)}$ куда ${\displaystyle w''(x+)}$ это ценность ${\displaystyle w''}$ на нижней границе верхнего сегмента, а ${\displaystyle w''(x-)}$ это ценность ${\displaystyle w''}$ у верхней границы нижнего сегмента. Когда значения конкретной производной не только непрерывны на границе, но и фиксированы, граничное условие записывается, например, ${\displaystyle \Delta w''=0^{*}}$ который фактически представляет собой два отдельных уравнения (например, ${\displaystyle w''(x-)=w''(x+)}$ = исправлено).

Граница	${\displaystyle w'''}$	${\displaystyle w''}$	${\displaystyle w'}$	${\displaystyle w}$
Зажим			${\displaystyle \Delta w'=0^{*}}$	${\displaystyle \Delta w=0^{*}}$
Простая поддержка		${\displaystyle \Delta w''=0}$	${\displaystyle \Delta w'=0}$	${\displaystyle \Delta w=0^{*}}$
Точечная сила	${\displaystyle \Delta w'''=\lambda }$	${\displaystyle \Delta w''=0}$	${\displaystyle \Delta w'=0}$	${\displaystyle \Delta w=0}$
Точечный крутящий момент	${\displaystyle \Delta w'''=0}$	${\displaystyle \Delta w''=\tau }$	${\displaystyle \Delta w'=0}$	${\displaystyle \Delta w=0}$
Свободный конец	${\displaystyle w'''=0}$	${\displaystyle w''=0}$
Зажим на конце			${\displaystyle w'}$ фиксированный	${\displaystyle w}$ фиксированный
Просто поддерживаемый конец		${\displaystyle w''=0}$		${\displaystyle w}$ фиксированный
Сила точки в конце	${\displaystyle w'''=\pm \lambda }$	${\displaystyle w''=0}$
Крутящий момент в конце	${\displaystyle w'''=0}$	${\displaystyle w''=\pm \tau }$

Обратите внимание, что в первых случаях, когда точечные силы и моменты расположены между двумя сегментами, существует четыре граничных условия: два для нижнего сегмента и два для верхнего. Когда силы и моменты приложены к одному концу балки, есть два граничных условия, которые применяются к этому концу. Знак точечных сил и моментов на конце будет положительным для нижнего конца и отрицательным для верхнего конца.

Рекомендации по загрузке

Приложенные нагрузки могут быть представлены либо через граничные условия, либо через функцию ${\displaystyle q(x,t)}$ который представляет собой внешнюю распределенную нагрузку. Использование распределенной загрузки часто способствует простоте. Однако граничные условия часто используются для моделирования нагрузок в зависимости от контекста; эта практика особенно распространена при анализе вибрации.

По своей природе распределенная нагрузка очень часто представляется кусочно, поскольку на практике нагрузка обычно не является непрерывной функцией. Точечные нагрузки можно моделировать с помощью Дельта-функция Дирака. Например, рассмотрим статическую однородную консольную балку длиной ${\displaystyle L}$ с направленной вверх нагрузкой ${\displaystyle F}$ наносится на свободный конец. Используя граничные условия, это можно смоделировать двумя способами. При первом подходе приложенная точечная нагрузка аппроксимируется поперечной силой, приложенной к свободному концу. В этом случае основное уравнение и граничные условия:

${\displaystyle {\begin{aligned}&EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=0\\&w|_{x=0}=0\quad ;\quad {\frac {\mathrm {d} w}{\mathrm {d} x}}{\bigg |}_{x=0}=0\quad ;\quad {\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}{\bigg |}_{x=L}=0\quad ;\quad -EI{\frac {\mathrm {d} ^{3}w}{\mathrm {d} x^{3}}}{\bigg |}_{x=L}=F\,\end{aligned}}}$

В качестве альтернативы мы можем представить точечную нагрузку как распределение с помощью функции Дирака. В этом случае уравнение и граничные условия имеют вид

${\displaystyle {\begin{aligned}&EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=F\delta (x-L)\\&w|_{x=0}=0\quad ;\quad {\frac {\mathrm {d} w}{\mathrm {d} x}}{\bigg |}_{x=0}=0\quad ;\quad {\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}{\bigg |}_{x=L}=0\,\end{aligned}}}$

Обратите внимание, что граничное условие поперечной силы (третья производная) удалено, иначе возникло бы противоречие. Это эквивалентные краевые задачи, и оба дают решение

${\displaystyle w={\frac {F}{6EI}}(3Lx^{2}-x^{3})\,~.}$

Приложение нескольких точечных нагрузок в разных местах приведет к ${\displaystyle w(x)}$ являясь кусочной функцией. Использование функции Дирака значительно упрощает такие ситуации; в противном случае балку пришлось бы разделить на секции, каждая с четырьмя граничными условиями, решаемыми отдельно. Хорошо организованное семейство функций, называемых Функции сингулярности часто используются как сокращение для функции Дирака, ее производная, и это первообразные.

Динамические явления также можно моделировать, используя уравнение статической балки, выбирая соответствующие формы распределения нагрузки. Например, бесплатный вибрация балки можно учесть с помощью функции нагрузки:

${\displaystyle q(x,t)=\mu {\frac {\partial ^{2}w}{\partial t^{2}}}\,}$

куда ${\displaystyle \mu }$ это линейная массовая плотность луча, не обязательно постоянным. С этой зависящей от времени нагрузкой уравнение балки будет уравнение в частных производных:

${\displaystyle {\frac {\partial ^{2}}{\partial x^{2}}}\left(EI{\frac {\partial ^{2}w}{\partial x^{2}}}\right)=-\mu {\frac {\partial ^{2}w}{\partial t^{2}}}.}$

Другой интересный пример описывает отклонение балки, вращающейся с постоянным угловая частота из ${\displaystyle \omega }$:

${\displaystyle q(x)=\mu \omega ^{2}w(x)\,}$

Это центростремительная сила распространение. Обратите внимание, что в этом случае ${\displaystyle q}$ является функцией смещения (зависимой переменной), и уравнение балки будет автономным обыкновенное дифференциальное уравнение.

Примеры

Трехточечный изгиб

В испытание на трехточечный изгиб классический эксперимент в механике. Он представляет собой случай, когда балка опирается на две роликовые опоры и подвергается сосредоточенной нагрузке, приложенной в середине балки. Сдвиг постоянен по абсолютной величине: он составляет половину центральной нагрузки P / 2. Он меняет знак в середине балки. Изгибающий момент изменяется линейно от одного конца, где он равен 0, и центра, где его абсолютное значение PL / 4, является наиболее важным риском разрыва. Деформация балки описывается полиномом третьей степени над половиной балки (вторая половина симметрична). Изгибающие моменты (${\displaystyle M}$), поперечные силы (${\displaystyle Q}$), а прогибы (${\displaystyle w}$) для балки, подвергающейся воздействию центральной точечной нагрузки, и асимметричной точечной нагрузки, приведены в таблице ниже.^[5]

Распределение	Максимум. ценить
Балка с простой опорой и центральной нагрузкой
${\displaystyle M(x)={\begin{cases}{\frac {Px}{2}},&{\mbox{for }}0\leq x\leq {\tfrac {L}{2}}\\{\frac {P(L-x)}{2}},&{\mbox{for }}{\tfrac {L}{2}}<x\leq L\end{cases}}}$	${\displaystyle M_{L/2}={\tfrac {PL}{4}}}$
${\displaystyle Q(x)={\begin{cases}{\frac {P}{2}},&{\mbox{for }}0\leq x\leq {\tfrac {L}{2}}\\{\frac {-P}{2}},&{\mbox{for }}{\tfrac {L}{2}}<x\leq L\end{cases}}}$	${\displaystyle |Q_{0}|=|Q_{L}|={\tfrac {P}{2}}}$
${\displaystyle w(x)={\begin{cases}-{\frac {Px(4x^{2}-3L^{2})}{48EI}},&{\mbox{for }}0\leq x\leq {\tfrac {L}{2}}\\{\frac {P(x-L)(L^{2}-8Lx+4x^{2})}{48EI}},&{\mbox{for }}{\tfrac {L}{2}}<x\leq L\end{cases}}}$	${\displaystyle w_{L/2}={\tfrac {PL^{3}}{48EI}}}$
Балка с простой опорой и асимметричной нагрузкой
${\displaystyle M(x)={\begin{cases}{\tfrac {Pbx}{L}},&{\mbox{for }}0\leq x\leq a\\{\tfrac {Pbx}{L}}-P(x-a)={\tfrac {Pa(L-x)}{L}},&{\mbox{for }}a<x\leq L\end{cases}}}$	${\displaystyle M_{B}={\tfrac {Pab}{L}}}$
${\displaystyle Q(x)={\begin{cases}{\tfrac {Pb}{L}},&{\mbox{for }}0\leq x\leq a\\{\tfrac {Pb}{L}}-P,&{\mbox{for }}a<x\leq L\end{cases}}}$	${\displaystyle Q_{A}={\tfrac {Pb}{L}}}$ ${\displaystyle Q_{C}={\tfrac {Pa}{L}}}$
${\displaystyle w(x)={\begin{cases}{\tfrac {Pbx(L^{2}-b^{2}-x^{2})}{6LEI}},&0\leq x\leq a\\{\tfrac {Pbx(L^{2}-b^{2}-x^{2})}{6LEI}}+{\tfrac {P(x-a)^{3}}{6EI}},&a<x\leq L\end{cases}}}$	${\displaystyle w_{\mathrm {max} }={\tfrac {{\sqrt {3}}Pb(L^{2}-b^{2})^{\frac {3}{2}}}{27LEI}}}$ в ${\displaystyle x={\sqrt {\tfrac {L^{2}-b^{2}}{3}}}}$

Консольные балки

Другой важный класс проблем включает: консоль балки. Изгибающие моменты (${\displaystyle M}$), поперечные силы (${\displaystyle Q}$), а прогибы (${\displaystyle w}$) для консольной балки, подверженной точечной нагрузке на свободном конце, и равномерно распределенной нагрузки приведены в таблице ниже.^[5]

Распределение	Максимум. ценить
Консольная балка с торцевой нагрузкой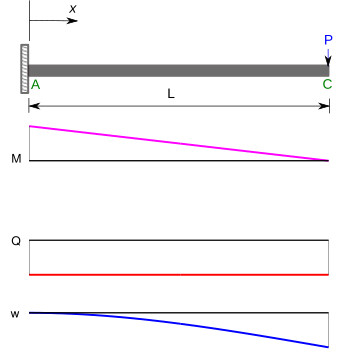
${\displaystyle M(x)=P(L-x)}$	${\displaystyle M_{A}=PL}$
${\displaystyle Q(x)=P}$	${\displaystyle Q_{\mathrm {max} }=P}$
${\displaystyle w(x)={\tfrac {Px^{2}(3L-x)}{6EI}}}$	${\displaystyle w_{C}={\tfrac {PL^{3}}{3EI}}}$
Консольная балка с равномерно распределенной нагрузкой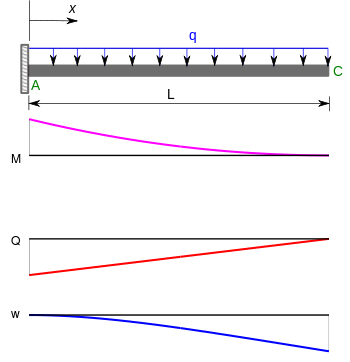
${\displaystyle M(x)=-{\tfrac {q(L^{2}-2Lx+x^{2})}{2}}}$	${\displaystyle M_{A}={\tfrac {qL^{2}}{2}}}$
${\displaystyle Q(x)=q(L-x),}$	${\displaystyle Q_{A}=qL}$
${\displaystyle w(x)={\tfrac {qx^{2}(6L^{2}-4Lx+x^{2})}{24EI}}}$	${\displaystyle w_{C}={\tfrac {qL^{4}}{8EI}}}$

Решения для нескольких других часто встречающихся конфигураций легко доступны в учебниках по механике материалов и технических справочниках.

Статически неопределимые балки

В изгибающие моменты и поперечные силы в пучках Эйлера – Бернулли часто можно определить напрямую, используя статический баланс силы и моменты. Однако при определенных граничных условиях количество реакций может превышать количество независимых уравнений равновесия.^[5] Такие балки называются статически неопределенный.

Встроенные балки, показанные на рисунке ниже, статически неопределимы. Для определения напряжений и прогибов таких балок наиболее прямым методом является решение уравнения Эйлера – Бернулли с соответствующими граничными условиями. Но прямые аналитические решения уравнения балки возможны только для простейших случаев. Поэтому для решения статически неопределимых задач пучка часто используются дополнительные методы, такие как линейное наложение.

Метод суперпозиции включает добавление решений ряда статически определенных задач, которые выбираются таким образом, что граничные условия для суммы отдельных задач складываются с граничными условиями исходной задачи.

(а) Равномерно распределенная нагрузка q.	(б) Линейно распределенная нагрузка с максимальной q0
${\displaystyle M_{\mathrm {max} }={\cfrac {qL^{2}}{12}}~;~~w_{\mathrm {max} }={\cfrac {qL^{4}}{384EI}}}$	${\displaystyle M_{\mathrm {max} }={\cfrac {qL^{2}}{300}}[3{\sqrt {30}}-10]~;~~w_{\mathrm {max} }={\cfrac {qL^{4}}{2500EI}}[75-7{\sqrt {105}}]}$
(c) Концентрированная нагрузка P	(d) Момент M0

Другой часто встречающейся проблемой статической неопределенности балки является консольная балка свободный конец опирается на ролик.^[5] Изгибающие моменты, поперечные силы и прогиб такой балки перечислены ниже:

Распределение	Максимум. ценить
${\displaystyle M(x)=-{\tfrac {q}{8}}(L^{2}-5Lx+4x^{2})}$	${\displaystyle {\begin{aligned}M_{B}&=-{\tfrac {9qL^{2}}{128}}{\mbox{ at }}x={\tfrac {5L}{8}}\\M_{A}&={\tfrac {qL^{2}}{8}}\end{aligned}}}$
${\displaystyle Q(x)=-{\tfrac {q}{8}}(8x-5L)}$	${\displaystyle Q_{A}=-{\tfrac {5qL}{8}}}$
${\displaystyle w(x)={\tfrac {qx^{2}}{48EI}}(3L^{2}-5Lx+2x^{2})}$	${\displaystyle w_{\mathrm {max} }={\tfrac {(39-55{\sqrt {33}})}{65,536}}{\tfrac {qL^{4}}{EI}}{\mbox{ at }}x={\tfrac {15-{\sqrt {33}}}{16}}L}$

Расширения

Кинематические допущения, на которых основана теория пучков Эйлера – Бернулли, позволяют распространить ее на более сложный анализ. Простое наложение позволяет выполнять трехмерную поперечную нагрузку. Использование альтернативы основные уравнения может позволить вязкоупругий или пластик деформация балки. Теория балок Эйлера – Бернулли может быть также распространена на анализ изогнутых балок, коробление балки, составные балки и геометрически нелинейный прогиб балки.

Теория пучков Эйлера – Бернулли не учитывает эффекты поперечного срезать напряжение. В результате он недооценивает отклонения и завышает собственные частоты. Для тонких балок (отношение длины балки к толщине порядка 20 или более) эти эффекты не имеют большого значения. Однако для толстых балок эти эффекты могут быть значительными. Более продвинутые теории пучка, такие как Теория пучка Тимошенко (разработан ученым российского происхождения Стивен Тимошенко ) были разработаны для учета этих эффектов.

Большие прогибы

Луч Эйлера – Бернулли

Исходная теория Эйлера – Бернулли справедлива только для бесконечно малые деформации и небольшие повороты. Теорию можно напрямую распространить на задачи с умеренно большими поворотами при условии, что деформация остается небольшой, с помощью фон Карман штаммы.^[7]

Гипотеза Эйлера – Бернулли о том, что плоские сечения остаются плоскими и перпендикулярными оси балки, приводят к смещениям вида

${\displaystyle u_{1}=u_{0}(x)-z{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}~;~~u_{2}=0~;~~u_{3}=w_{0}(x)}$

Используя определение лагранжевой деформации Грина из теория конечных деформаций, мы можем найти фон Карман штаммы для балки, которые действительны для больших вращений, но малых деформаций. Эти штаммы имеют вид

${\displaystyle {\begin{aligned}\varepsilon _{11}&={\cfrac {\mathrm {d} u_{0}}{dx}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}+{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\right)^{2}+\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]\\\varepsilon _{22}&=0\\\varepsilon _{33}&={\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\\\varepsilon _{23}&=0\\\varepsilon _{31}&={\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}-{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)-{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\right)\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)\right]\\\varepsilon _{12}&=0\end{aligned}}}$

От принцип виртуальной работы, баланс сил и моментов в балках дает нам уравнения равновесия

${\displaystyle {\begin{aligned}{\cfrac {\mathrm {d} N_{xx}}{\mathrm {d} x}}+f(x)&=0\\{\cfrac {\mathrm {d} ^{2}M_{xx}}{\mathrm {d} x^{2}}}+q(x)+{\cfrac {\mathrm {d} }{\mathrm {d} x}}\left(N_{xx}{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)&=0\end{aligned}}}$

куда ${\displaystyle f(x)}$ осевая нагрузка, ${\displaystyle q(x)}$ - поперечная нагрузка, а

${\displaystyle N_{xx}=\int _{A}\sigma _{xx}~\mathrm {d} A~;~~M_{xx}=\int _{A}z\sigma _{xx}~\mathrm {d} A}$

Чтобы замкнуть систему уравнений, нам понадобится основные уравнения которые связывают напряжения с деформациями (и, следовательно, напряжения с перемещениями). Для больших вращений и малых деформаций эти соотношения имеют вид

${\displaystyle {\begin{aligned}N_{xx}&=A_{xx}\left[{\cfrac {\mathrm {d} u_{0}}{dx}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-B_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\\M_{xx}&=B_{xx}\left[{\cfrac {du_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-D_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\end{aligned}}}$

куда

${\displaystyle A_{xx}=\int _{A}E~\mathrm {d} A~;~~B_{xx}=\int _{A}zE~\mathrm {d} A~;~~D_{xx}=\int _{A}z^{2}E~\mathrm {d} A~.}$

Количество ${\displaystyle A_{xx}}$ это жесткость на растяжение,${\displaystyle B_{xx}}$ это спаренный жесткость на изгиб при растяжении, и ${\displaystyle D_{xx}}$ это жесткость на изгиб.

Для ситуации, когда балка имеет однородное поперечное сечение и не имеет осевой нагрузки, основное уравнение для балки Эйлера – Бернулли с большим вращением имеет вид

${\displaystyle EI~{\cfrac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}-{\frac {3}{2}}~EA~\left({\cfrac {\mathrm {d} w}{\mathrm {d} x}}\right)^{2}\left({\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q(x)}$

Смотрите также

• Прикладная механика
• Гибка
• Изгибающий момент
• Коробление
• Жесткость на изгиб
• Обобщенная теория пучка
• Теория пластин
• Теория сэндвичей
• Диаграмма сдвига и момента
• Функция сингулярности
• Штамм (материаловедение)
• Теория пучка Тимошенко
• Теорема трех моментов (Теорема Клапейрона)
• Испытание на трехточечный изгиб

Примечания

1. Для балки Эйлера – Бернулли без осевой нагрузки эта ось называется нейтральная ось.

Рекомендации

1. Тимошенко, С., (1953), История прочности материалов, Макгроу-Хилл, Нью-Йорк
2. Трусделл, К. (1960), Рациональная механика гибких или упругих тел 1638–1788 гг., Выставка Venditioni Orell Fussli Turici.
3. Балларини, Роберто (18 апреля 2003 г.). "Теория пучка да Винчи-Эйлера-Бернулли?". Интернет-журнал "Машиностроение". Архивировано из оригинал 23 июня 2006 г.. Получено 2006-07-22.
4. Сеон М. Хан, Хайм Бенаройя и Тимоти Вей (22 марта 1999 г.). «Динамика поперечно колеблющихся балок с использованием четырех инженерных теорий» (PDF). Окончательный версия. Академическая пресса. Архивировано из оригинал (PDF) 20 июля 2011 г.. Получено 2007-04-15.
5. Гир Дж. М. и Тимошенко С. П., 1997 г. Механика материалов, Издательство PWS.
6. Кареста, Мауро. «Колебания свободного луча» (PDF). Получено 2019-03-20.
7. Редди, Дж. Н. (2007), Нелинейный анализ методом конечных элементов, Oxford University Press.

• Э. А. Витмер (1991–1992). "Элементарная теория пучка Бернулли-Эйлера". Примечания к унифицированному инженерному курсу MIT. С. 5–114–5–164.

внешняя ссылка

• Напряжение и прогиб балки, таблицы прогиба балки