Упражнение (математика) - Exercise (mathematics)

А математическое упражнение рутинное приложение алгебры или другой математики к поставленной задаче. Учителя математики назначать математические упражнения для развития навыков своих учеников. Ранние упражнения имеют дело с добавление, вычитание, умножение, и разделение из целые числа. Обширные курсы упражнений в школа продлить такой арифметика к рациональное число. Различные подходы к геометрия основывались на упражнениях на отношения углов, отрезков и треугольников. Тема тригонометрия получает много упражнений от тригонометрические тождества. В колледже упражнения по математике часто зависят от функции реальной переменной или применения теоремы. Стандартные упражнения исчисление включать поиск производные и интегралы указанных функций.

Обычно инструкторы готовят студентов с отработанные примеры: сформулировано упражнение, затем дается типовой ответ. Часто перед тем, как ученики подготовятся к самостоятельному выполнению упражнений, демонстрируется несколько рабочих примеров. Некоторые тексты, например, в Очертания Шаума, сосредоточьтесь на рабочих примерах, а не на теоретическом рассмотрении математической темы.

Выпускной

В соответствии с Лев Выготский соответствующие упражнения находятся в зоне, где ученики могут выполнить задание под руководством

В начальной школе ученики начинают с одиночного цифра арифметические упражнения. Позже в большинстве упражнений используются как минимум две цифры. Обычное упражнение в элементарная алгебра призывает к факторизация из многочлены. Еще одно упражнение завершение квадрата в трехчлене. Искусственно созданный проблема со словом это жанр упражнений, призванный поддерживать актуальность математики. Стивен Ликок описал этот тип:[1]

Изучающий арифметику, который овладел первыми четырьмя правилами своего искусства и успешно борется с суммами и дробями, сталкивается с непрерывным пространством вопросов, известных как проблемы. Это рассказы о приключениях и трудолюбии с опущенным концом, которые, хотя и выявляют сильное семейное сходство, не лишены определенного элемента романтики.

Различие между упражнением и математическая проблема был сделан Аланом Х. Шенфельдом:[2]

Студенты должны овладеть соответствующим предметом, и для этого подходят упражнения. Но если механические упражнения - единственные проблемы, которые студенты видят на своих занятиях, мы оказываем студентам медвежью услугу.

Он выступал за постановку задач:

Под «реальными проблемами» ... я имею в виду математические задачи, которые бросают вызов ученику и над которыми ученик должен работать, чтобы найти решение.

Аналогичное мнение было высказано Марвином Биттингером, когда он готовил второе издание.[3] его учебника:

В ответ на комментарии пользователей авторы добавили упражнения, которые требуют от ученика чего-то другого, кроме понимания непосредственных целей данного урока, но не обязательно являются очень сложными.

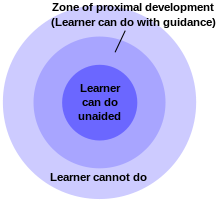
В зона ближайшего развития для каждого ученика или группы учеников устанавливает упражнения на уровне сложности, который бросает им вызов, но не мешает им.

Некоторые комментарии в предисловии к учебнику по математическому анализу[4] покажите центральное место упражнений в книге:

Упражнения составляют около четверти текста - на наш взгляд, наиболее важную часть текста. ... Дополнительные упражнения в конце каждой главы дополняют другие наборы упражнений и предоставляют совокупные упражнения, требующие навыков из предыдущих глав.

Этот текст включает «Функции и графики в приложениях» (глава 0.6), представляющий собой четырнадцать страниц для подготовки к решению текстовых задач.

Авторы книги по конечные поля свободно выбирали упражнения:[5]

Чтобы повысить привлекательность этой книги как учебник, мы включили отработанные примеры в соответствующие места в тексте и включили списки упражнений для глав 1 - 9. Эти упражнения варьируются от обычных задач до альтернативных. доказательства ключевых теорем, но содержащие также материал, выходящий за рамки того, что описано в тексте.

Дж. К. Максвелл объяснил, как упражнения облегчают доступ к язык математики:[6]

Как математики мы выполняем определенные мысленные операции над символами числа или количества, и, шаг за шагом переходя от более простых к более сложным операциям, мы можем выразить одно и то же во многих различных формах. Эквивалентность этих различных форм, хотя и является необходимым следствием самоочевидных аксиом, не всегда, на наш взгляд, самоочевидна; но математик, который в результате долгой практики познакомился со многими из этих форм и стал экспертом в процессах, ведущих от одной к другой, часто может преобразовать озадачивающее выражение в другое, объясняющее его значение на более понятном языке.

Фирменные наборы

Индивидуальные преподаватели в различных колледжах используют упражнения как часть своих курсов математики. Расследование решение проблем в университетах, Шенфельд отмечал:[7]

Предложения для старших классов по математике, где по большей части студенты работали над сборниками задач, которые были составлены их индивидуальными преподавателями. На таких курсах упор делался на обучение на практике, без попытки преподать конкретную эвристику: студенты работали над множеством задач, потому что (согласно неявной учебной модели, лежащей в основе таких курсов), именно так можно добиться хороших результатов в математике.

Такие сборники упражнений могут быть проприетарный инструктору и его учреждению. В качестве примера ценности наборов упражнений рассмотрим выполнение Тору Кумон и его Кумон метод. В своей программе ученик не приступает к выполнению каждого уровня упражнения. На Русская математическая школа, учащиеся приступают к выполнению многоэтапных задач уже в первом классе, учатся использовать предыдущие результаты для продвижения к решению.

В 1960-х годах сборники математических упражнений были переведены с русский и опубликовано В. Х. Фриман и компания: Сборник задач олимпиады СССР (1962),[8] Задачи по высшей алгебре (1965),[9] и Задачи в дифференциальных уравнениях (1963).[10]

История

В Китае с древних времен счетные стержни использовались для представления чисел, а арифметика выполнялась с стержневой камень а позже Suanpan. В Книга о числах и вычислениях и Девять глав по математическому искусству включать упражнения, которые являются образцами линейная алгебра.[11]

Около 980 г. Ас-Сиджи написал его Способы облегчения построения геометрических фигур, который был переведен и опубликован Ян Хогендейк в 1996 г.[12]

An арабский язык сборник упражнений был переведен на испанский как Compendio de Algebra de Abenbéder и рассмотрен в Природа.[13]

В Европе до 1900 г. графическая перспектива обрамленные геометрические упражнения. Например, в 1719 г. Брук Тейлор написал в Новые принципы линейной перспективы

[Читатель] найдет гораздо больше удовольствия, наблюдая, насколько обширны эти Принципы, применяя их к конкретным случаям, которые он сам придумает, пока он упражняется в этом Искусстве ...[14]

Тейлор продолжил

... истинный и лучший способ изучить любое искусство - это не видеть множества примеров, выполненных другим человеком; но сначала овладеть Принципами этого, а затем знакомить их, упражняя себя в Практике.[15]

Использование письменные доски в школах предусмотрен ранний формат упражнений. Рост числа программ упражнений последовал за введением письменных экзаменов и обучения на бумаге и ручке.

Феликс Кляйн описал подготовку к вступительный экзамен из École Polytechnique в качестве[16]

... курс "mathematiques especiales". Это необычайно сильная концентрация математического образования - до 16 часов в неделю, в котором элементарная аналитическая геометрия и механика, а недавно и исчисление бесконечно малых, тщательно изучаются и превращаются в надежно освоенный инструмент с помощью множества упражнений.

Сильвестр Лакруа был одаренным учителем и толкователем. В его книге по начертательной геометрии используются разделы, обозначенные как «Проблема», чтобы улучшить понимание читателя. В 1816 году он написал Очерки преподавания в целом и преподавания математики в частности которые подчеркнули необходимость упражнений и тестов:

Экзаменатор, вынужденный в краткосрочной перспективе умножить свои вопросы настолько, чтобы охватить те предметы, которые он задает, до большей части преподаваемого материала не может быть менее тщательным, поскольку, если, сокращая, он откладывает заявки в сторону, он таким образом ничего не выиграет для школьных факультетов.[17]

Эндрю Варвик обратил внимание на исторический вопрос об упражнениях:

Включение иллюстративных упражнений и задач в конце глав в учебники математической физики стало сейчас настолько обычным явлением, что может показаться обычным делом, но важно понимать, что этот педагогический прием возник относительно недавно и был введен в конкретном историческом контексте.[18]:168

В отчетности Математические трипосы экзамены, введенные в Кембриджский университет, он отмечает

Такое кумулятивное соревновательное обучение также более эффективно осуществлялось частными репетиторами, использующими индивидуальное обучение, специально подготовленные рукописи, оцененные примеры и задачи, чем преподаватели колледжей, проводившие большие классы с посредственными темпами.[18]:79

Объясняя связь экзамена и упражнения, он пишет:

... к 1830-м годам именно проблемы на экзаменационных листах, а не упражнения в учебниках, определяли стандарт, к которому стремились амбициозные студенты ... [студенты Кембриджа] не только ожидали найти свой путь через простейший набросок примера. , но их учили рассматривать такие упражнения как полезную подготовку к решению сложных задач на экзаменах.[18]:152

Объясняя, как реформа прижилась, Уорвик писал:

В Кембридже было широко распространено мнение, что лучший способ преподавания математики, в том числе новым аналитическим методам, - это практические примеры и задачи, и к середине 1830-х годов некоторые из первого поколения молодых студентов колледжей обучались более высокому анализу. таким образом, начали проводить свои собственные исследования и быть назначенными экзаменаторами Tripos.[18]:155

Warwick сообщает, что в Германии Франц Эрнст Нойман примерно в то же время «разработал общую систему градуированных упражнений, которая познакомила учащихся с иерархией основных математических навыков и методов, и ... начал конструировать свои собственные наборы задач через которую его ученики могли научиться своему ремеслу ».[18]:174 В России, Стивен Тимошенко реформированная инструкция по упражнениям. В 1913 году он преподавал сопротивление материалов в Петербургский государственный университет путей сообщения. Как он писал в 1968 году,

[Практические] упражнения в институте не проводились, а на экзаменах студентам задавались только теоретические вопросы из принятого учебника. Мне пришлось как можно скорее положить конец подобному обучению. Студенты четко понимали ситуацию, осознавали необходимость лучшего усвоения предмета и не возражали против сильного увеличения нагрузки. Основная трудность была с учителями, точнее, с экзаменаторами, которые привыкли основывать свои экзамены на книге. Постановка практических задач на экзаменах усложняла их работу. Они были людьми годами ... единственная надежда заключалась в том, чтобы привлечь к обучению молодых людей.[19]

Смотрите также

Рекомендации

  1. ^ Стивен Ликок «A, B, C - Человеческий элемент в математике», страницы 131–55 в Математическая сорока (1962) автор Клифтон Фадиман (редактор) Саймон и Шустер
  2. ^ Алан Х. Шенфельд (1988) «Решение проблем» (см. Стр. 85), глава 5 Математическое образование в средних школах и двухгодичных колледжах Пол Дж. Кэмпбелл и Луи С. Гринштейн, издательство Garland Publishing, ISBN  0-8240-8522-1
  3. ^ Марвин Л. Биттингер (1981) Фундаментальная алгебра и тригонометрия, 2-е издание, Эддисон Уэсли, ISBN  0-201-03839-0
  4. ^ Л. Дж. Гольдштейн, Д. К. Лэй, Д. И. Шнайдер (1993) Исчисление и его приложения, 6-е издание, Prentice Hall, ISBN  0-13-117169-0
  5. ^ Р. Лидл и Х. Нидеррайтер (1986) Введение в конечные поля и их приложения, стр. viii, Издательство Кембриджского университета
  6. ^ Дж. К. Максвелл (1890) Научные статьи Джеймса Клерка Максвелла, том 2, В. Д. Нивен редактор, стр. 216, через Интернет-архив
  7. ^ Schoenfeld 1988, стр. 82
  8. ^ ДЕЛАТЬ. Шкланский, Н. Четцов и Яглом И. М., перевод Джона Майковича, редакция Ирвинга Сассмана, Сборник задач олимпиады СССР, W.H. Freeman and Company
  9. ^ Д. К. Фаддеев & ЯВЛЯЕТСЯ. Соминский, перевод Джоэл Ли Бреннер (1965) Задачи по высшей алгебре, W.H. Freeman & Company
  10. ^ Алексей Федорович Филиппов, переводчик и редактор Дж. Л. Бреннер (1963,6) Задачи в дифференциальных уравнениях, W.H. Freeman
  11. ^ Харт, Роджер (2010). Китайские корни линейной алгебры. JHU Press. ISBN  9780801899584.
  12. ^ Ян Хогендейк (1996) Способы облегчения построения геометрических фигур к Ас-Сиджи
  13. ^ Г. Б. Мэтьюз (1917) Compendio de Algebra de Abenbéder из Природа 98:466,7 (#2465).
  14. ^ Брук Тейлор (1719) Новые принципы линейной перспективы, Предисловие, стр. Vi, как указано в Кирсти Андерсен (1992) Работа Брука Тейлора о линейной перспективе, стр 152, Спрингер, ISBN  0-387-97486-5
  15. ^ Тейлор, стр. VII, Андерсен, стр. 153
  16. ^ Феликс Кляйн, Переводчик М. Акермана (1979) Развитие математики в XIX веке, стр 59, Math Sci Press
  17. ^ С. Ф. Лакруа (1816) Essais sur l’enseignement en general, et sur celui des mathematiques en special, стр. 201
  18. ^ а б c d е Эндрю Уорвик (2003) Магистр теории: Кембридж и рост математической физики, Издательство Чикагского университета ISBN  0-226-87375-7
  19. ^ Стивен Тимошенко (1968) Насколько я помню, Переводчик Роберта Аддиса, стр. 133,4, Компания D. Van Nostrand

внешняя ссылка