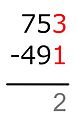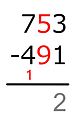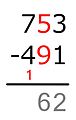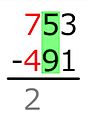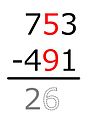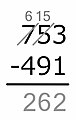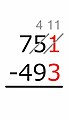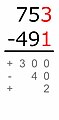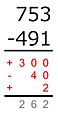Вычитание - Subtraction - Wikipedia

"5 − 2 = 3 "(устно:" пять минус два равно трем ")

Плакат возле магазина в Бордо вычет рекламы 20% от стоимости второго купленного парфюма.

Вычитание является арифметическая операция который представляет собой операцию удаления объектов из коллекции. Результат вычитания называется разница. Вычитание обозначается знак минус, −. Например, на соседней картинке есть 5 − 2 яблоки - это означает, что 5 яблок из которых убраны 2, в результате получается 3 яблока. Следовательно разница из 5 и 2 равно 3, то есть 5 − 2 = 3. Хотя в первую очередь связаны с натуральными числами в арифметика, вычитание также может представлять собой удаление или уменьшение физических и абстрактных величин с использованием различных типов объектов, включая отрицательные числа, фракции, иррациональные числа, векторов, десятичные дроби, функции и матрицы.^[1][2]

Вычитание следует нескольким важным схемам. это антикоммутативный, что означает, что изменение порядка меняет знак ответа. Это тоже не ассоциативный, что означает, что при вычитании более двух чисел имеет значение порядок, в котором выполняется вычитание. Потому что 0 это аддитивная идентичность, вычитание не меняет числа. Вычитание также подчиняется предсказуемым правилам относительно связанных операций, таких как добавление и умножение. Все эти правила могут быть доказано, начиная с вычитания целые числа и обобщая действительные числа и дальше. Общий бинарные операции которые следуют этим шаблонам, изучаются в абстрактная алгебра.

Вычитание натуральных чисел - одна из самых простых числовых задач. Маленьким детям доступно вычитание очень маленьких чисел. В начальное образование например, студентов учат вычитать числа в десятичный система, начиная с однозначных чисел и постепенно решая более сложные проблемы.

В продвинутой алгебре и в компьютерная алгебра, выражение, включающее вычитание, например А − B обычно рассматривается как сокращенное обозначение для добавления А + (−B). Таким образом, А − B содержит два термина, а именно А и -B. Это позволяет упростить использование ассоциативность и коммутативность.

Обозначения и терминология

Вычитание чисел 0–10. Метки линий = уменьшенное. Ось X = вычитание. Ось Y = разница.

Вычитание обычно пишется с использованием знак минус «-» между терминами;^[3] то есть в инфиксная запись. Результат выражается знак равенства. Например,

${\displaystyle 2-1=1}$ (произносится как «два минус один равно одному»)

${\displaystyle 4-2=2}$ (произносится как «четыре минус два равно два»)

${\displaystyle 6-3=3}$ (произносится как «шесть минус три равно трем»)

${\displaystyle 4-6=-2}$ (произносится как «четыре минус шесть равняется двум минусам»)

Также существуют ситуации, когда вычитание «понимается», даже если символ не появляется:

• Столбец из двух чисел, нижнее число которого выделено красным, обычно указывает на то, что меньшее число в столбце должно быть вычтено, а разница, указанная ниже, под линией. Это наиболее распространено в бухгалтерском учете.

Формально вычитаемое число известно как вычитаемое,^[4][5] в то время как число, из которого оно вычитается, является уменьшаемое.^[4][5] В результате разница.^[4][5][2][6]

Вся эта терминология происходит от латинский. "Вычитание " является английский слово происходит от латинского глагол вычитать, что, в свою очередь, является сложный из суб "из-под" и Trahere "тянуть". Таким образом, вычесть - значит рисовать снизу, или в забрать.^[7] С использованием герундий суффикс -й приводит к «вычитаем», «вещь, которую нужно вычесть».^[а] Точно так же из minuere «уменьшать или уменьшать» получается «уменьшать», что означает «вещь, которую нужно уменьшить».

Целых и действительных чисел

Целые числа

Представьте себе отрезок из длина б с надписью на левом конце а и правый конец помечен c.Начиная с а, занимает б шаги вправо, чтобы добраться c. Это движение вправо математически моделируется добавление:

а + б = c.

Из c, занимает б шаги к оставили вернуться к а. Это движение влево моделируется вычитанием:

c − б = а.

Теперь сегмент линии с цифрами 1, 2, и 3. Из позиции 3 не нужно делать шагов влево, чтобы оставаться в позиции 3, поэтому 3 − 0 = 3. Чтобы попасть в позицию 1, нужно сделать 2 шага влево, поэтому 3 − 2 = 1. Этот рисунок неадекватен для описания того, что произойдет после перехода на 3 шага влево от позиции 3. Чтобы представить такую ​​операцию, линию необходимо удлинить.

Чтобы вычесть произвольное натуральные числа, начинается строка, содержащая каждое натуральное число (0, 1, 2, 3, 4, 5, 6, ...). От 3 требуется 3 шага влево, чтобы добраться до 0, поэтому 3 − 3 = 0. Но 3 − 4 по-прежнему недействителен, так как снова покидает строку. Натуральные числа не подходят для вычитания.

Решение состоит в том, чтобы рассмотреть целое число числовая строка (..., −3, −2, −1, 0, 1, 2, 3, ...). Таким образом, чтобы добраться до −1, нужно сделать 4 шага влево от 3:

3 − 4 = −1.

Натуральные числа

Вычитание натуральные числа не является закрыто: разница не является натуральным числом, если минус не больше или не равен вычитаемому. Например, 26 нельзя вычесть из 11, чтобы получить натуральное число. В таком случае используется один из двух подходов:

1. Сделайте вывод, что 26 нельзя вычесть из 11; вычитание становится частичная функция.
2. Дайте ответ как целое число представляющий отрицательное число, поэтому результат вычитания 26 из 11 равен −15.

Действительные числа

Вычитание действительных чисел определяется как сложение чисел со знаком. В частности, число вычитается путем добавления его Противоположное число, как и в случае 3 - π = 3 + (−π). Это помогает сохранить звенеть действительных чисел "просто", избегая введения "новых" операторов, таких как вычитание. Обычно на кольце определены только две операции; в случае целых чисел это сложение и умножение. В кольце уже есть понятие аддитивных инверсий, но в нем нет понятия отдельной операции вычитания, поэтому использование сложения со знаком в качестве вычитания позволяет применить аксиомы кольца к вычитанию - без необходимости что-либо доказывать.

Характеристики

Антикоммутативность

Вычитание антикоммутативный, что означает, что если переставить члены в разнице слева направо, результат будет отрицательным по сравнению с исходным результатом. Символически, если а и б любые два числа, то

а − б = −(б − а).

Неассоциативность

Вычитание неассоциативный, который возникает, когда кто-то пытается определить повторное вычитание. В общем, выражение

"а − б − c"

может быть определено как означающее либо (а − б) − c или же а − (б − c), но эти две возможности приводят к разным ответам. Чтобы решить эту проблему, необходимо установить порядок действий, причем разные порядки дают разные результаты.

Предшественник

В контексте целых чисел вычитание один тоже играет особую роль: для любого целого а, целое число (а − 1) это наибольшее целое число меньше, чем а, также известный как предшественник а.

Меры измерения

При вычитании двух чисел с такими единицами измерения, как килограммы или же фунты, у них должен быть один и тот же блок. В большинстве случаев разница будет в той же единице, что и исходные числа.

Проценты

Изменения в проценты можно сообщить как минимум в двух формах, процентное изменение и процентный пункт изменять. Процентное изменение представляет собой относительное изменение между двумя величинами в процентах, а процентный пункт изменение - это просто число, полученное вычитанием двух процентов.^[8][9][10]

В качестве примера предположим, что 30% виджетов, изготовленных на заводе, неисправны. Спустя полгода неисправны 20% виджетов. Процентное изменение 20% − 30%/30% = −1/3 = −33+1/3%, а изменение в процентных пунктах составляет -10 процентных пунктов.

В вычислениях

В метод дополнений это метод, используемый для вычитания одного числа из другого, используя только положительные числа. Этот метод обычно использовался в механические калькуляторы, и до сих пор используется в современных компьютеры.

Двоичный цифра	Единицы дополнять
0	1
1	0

Чтобы вычесть двоичное число у (вычитаемое) из другого числа Икс (minuend), единственное дополнение у добавлен к Икс и к сумме добавляется один. После этого первая цифра результата "1" отбрасывается.

Метод дополнений особенно полезен в двоичной системе счисления (основание 2), поскольку дополнение единиц очень легко получить инвертированием каждого бита (изменением «0» на «1» и наоборот). И добавление 1 для получения двух дополнений может быть выполнено путем имитации переноса в младший бит. Например:

  01100100 (x, равно 100 в десятичной системе) - 00010110 (y, равно 22 в десятичной системе)

становится суммой:

  01100100 (x) + 11101001 (дополнение до единиц y) + 1 (для получения дополнения до двух) —————————— 101001110

Если отбросить начальную «1», получим ответ: 01001110 (равно 78 в десятичной системе).

Обучение вычитанию в школах

Методы, используемые для обучения вычитанию Начальная школа варьируются от страны к стране, и внутри страны в разное время применяются разные методы. В том, что известно в США как традиционная математика, в конце 1-го года (или в течение 2-го года) учащихся преподают конкретный процесс для использования с многозначными целыми числами, и он расширен в четвертом или пятом классе, чтобы включить десятичные представления дробных чисел.

В Америке

В настоящее время почти во всех американских школах преподается метод вычитания с использованием заимствования или перегруппировки (алгоритм разложения) и система маркировки, называемая костылями.^[11][12] Хотя метод заимствования был известен и ранее публиковался в учебниках, использование костылей в американских школах распространилось после Уильям А. Браунелл опубликовали исследование, в котором утверждалось, что костыли полезны для студентов, использующих этот метод.^[13] Эта система быстро прижилась, вытеснив другие методы вычитания, использовавшиеся в то время в Америке.

В Европе

Некоторые европейские школы используют метод вычитания, называемый австрийским методом, также известный как метод сложения. В этом методе нет заимствования. Есть также костыли (маркировка для улучшения памяти), которые различаются в зависимости от страны.^[14][15]

Сравнение двух основных методов

Оба эти метода разделяют вычитание как процесс вычитания одной цифры по разряду. Начиная с наименьшей значащей цифры, вычитание вычитания:

s_j s_j−1 ... s₁

от minuend

м_k м_k−1 ... м₁,

где каждый s_я и м_я это цифра, начинается путем записи м₁ − s₁, м₂ − s₂и т. д., пока s_я не превышает м_я. Иначе, м_я увеличивается на 10, а некоторые другие цифры изменяются, чтобы скорректировать это увеличение. Американский метод исправляет, пытаясь уменьшить уменьшенную цифру м_я+1 на единицу (или продолжая заимствование влево до тех пор, пока не будет отличная от нуля цифра, из которой заимствовать). Европейский метод исправляет за счет увеличения вычитаемой цифры s_я+1 одним.

Пример: 704 − 512.

${\displaystyle {\begin{array}{rrrr}&\color {Red}-1\\&C&D&U\\&7&0&4\\&5&1&2\\\hline &1&9&2\\\end{array}}{\begin{array}{l}{\color {Red}\longleftarrow {\rm {carry}}}\\\\\longleftarrow \;{\rm {Minuend}}\\\longleftarrow \;{\rm {Subtrahend}}\\\longleftarrow {\rm {Rest\;or\;Difference}}\\\end{array}}}$

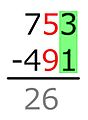
Уменьшаемое - 704, вычитаемое - 512. Уменьшаемые цифры - м₃ = 7, м₂ = 0 и м₁ = 4. Вычитаемые цифры s₃ = 5, s₂ = 1 и s₁ = 2. Начиная с места, 4 не меньше 2, поэтому разница 2 записывается на место результата. В разряде десятков 0 меньше 1, поэтому 0 увеличивается на 10, а разница с 1, то есть 9, записывается в разряде десятков. Американский метод исправляет увеличение десяти, уменьшая цифру в разряде сотен уменьшаемого числа на единицу. То есть 7 вычеркивается и заменяется на 6. Затем вычитание продолжается в разряде сотен, где 6 не меньше 5, поэтому разница записывается в разряде сотен результата. Готово, результат - 192.

Австрийский метод не уменьшает 7 до 6. Скорее он увеличивает вычитаемую сотню на единицу. Рядом или ниже этой цифры делается небольшая отметка (в зависимости от школы). Затем вычитание продолжается, спрашивая, какое число при увеличении на 1, и 5 прибавляется к нему, дает 7. Ответ - 1, и записывается в разряде сотен результата.

Есть еще одна тонкость: в американском методе ученик всегда использует мысленную таблицу вычитания. Австрийский метод часто побуждает ученика мысленно использовать таблицу сложения в обратном порядке. В приведенном выше примере, вместо того, чтобы прибавлять 1 к 5, получать 6 и вычитать это из 7, ученика просят подумать, какое число при увеличении на 1 и добавлении 5 дает 7.

Вычитание вручную

Австрийский метод

Пример:

• 

  1 + ... = 3

• 

  Разница написана под чертой.

• 

  9 + ... = 5
  Требуемая сумма (5) слишком мала.

• 

  Итак, мы прибавляем к нему 10 и ставим 1 под следующим более высоким знаком вычитаемого числа.

• 

  9 + ... = 15
  Теперь мы можем найти разницу, как и раньше.

• 

  (4 + 1) + ... = 7

• 

  Разница написана под чертой.

• 

  Полная разница.

Вычитание слева направо

Пример:

• 

  7 − 4 = 3
  Этот результат только карандашом.

• 

  Поскольку следующая цифра уменьшаемого числа меньше, чем вычитаемое, мы вычитаем единицу из нашего числа, начерченного карандашом, и мысленно прибавляем десять к следующему.

• 

  15 − 9 = 6

• 

  Поскольку следующая цифра в уменьшаемом не меньше, чем вычитаемое, мы сохраняем это число.

• 

  3 − 1 = 2

Американский метод

В этом методе каждая цифра вычитаемого вычитается из цифры над ней, начиная справа налево. Если верхнее число слишком мало, чтобы вычесть из него нижнее число, мы добавляем к нему 10; эта 10 «заимствована» из верхней цифры слева, из которой мы вычитаем 1. Затем мы переходим к вычитанию следующей цифры и заимствованию по мере необходимости, пока не будет вычтена каждая цифра.

• 

  3 − 1 = ...

• 

  Пишем разницу под чертой.

• 

  5 − 9 = ...
  Minuend (5) слишком мал!

• 

  Итак, прибавляем к нему 10. 10 "заимствовано" из цифры слева, которая уменьшается на 1.

• 

  15 − 9 = ...
  Теперь вычитание работает, и мы пишем разницу под чертой.

• 

  6 − 4 = ...

• 

  Пишем разницу под чертой.

• 

  Полная разница.

Торговля в первую очередь

Вариант американского метода, при котором все заимствования производятся до вычитания.^[16]

Пример:

• 

  1 - 3 = невозможно.
  Мы добавляем 10 к 1. Поскольку 10 «позаимствовано» у ближайших 5, 5 понижается на 1.

• 

  4 - 9 = невозможно.
  Итак, действуем как в шаге 1.

• 

  Работаем справа налево:
  11 − 3 = 8

• 

  14 − 9 = 5

• 

  6 − 4 = 2

Частичные различия

Метод частичных разностей отличается от других методов вертикального вычитания, потому что не происходит заимствования или переноса. Вместо них ставятся знаки плюс или минус в зависимости от того, меньше или больше уменьшаемое, чем вычитаемое. Сумма частичных разностей и есть общая разница.^[17]

Пример:

• 

  Меньшее число вычитается из большего:
  700 − 400 = 300
  Поскольку уменьшаемое значение больше, чем вычитаемое, эта разница имеет знак плюс.

• 

  Меньшее число вычитается из большего:
  90 − 50 = 40
  Поскольку уменьшаемое меньше, чем вычитаемое, эта разница имеет знак минус.

• 

  Меньшее число вычитается из большего:
  3 − 1 = 2
  Поскольку уменьшаемое значение больше, чем вычитаемое, эта разница имеет знак плюс.

• 

  +300 − 40 + 2 = 262

Невертикальные методы

Подсчет

Вместо того, чтобы находить разность цифр за цифрой, можно подсчитать числа между вычитаемым и уменьшаемым.^[18]

Пример: 1234 - 567 = можно найти, выполнив следующие действия:

• 567 + 3 = 570
• 570 + 30 = 600
• 600 + 400 = 1000
• 1000 + 234 = 1234

Сложите значение каждого шага, чтобы получить общую разницу: 3 + 30 + 400 + 234 = 667.

Прекращение вычитания

Другой метод, который полезен для счет в уме состоит в том, чтобы разделить вычитание на небольшие шаги.^[19]

Пример: 1234 - 567 = можно решить следующим образом:

• 1234 − 500 = 734
• 734 − 60 = 674
• 674 − 7 = 667

То же изменение

Тот же метод изменения использует тот факт, что добавление или вычитание одного и того же числа из уменьшаемого и вычитаемого не меняет ответ. Просто добавляем сумму, необходимую для получения нулей при вычитании.^[20]

Пример:

«1234 - 567 =» можно решить следующим образом:

• 1234 − 567 = 1237 − 570 = 1267 − 600 = 667

Смотрите также

• Декремент
• Элементарная арифметика
• Метод дополнений
• Отрицательное число
• Знаки плюс и минус

Примечания

1. «Subtrahend» сокращается с помощью флективного латинского суффикса -us, например остающийся не отклоненным как в numerus subtrahendus «число, которое нужно вычесть».

Рекомендации

1. «Исчерпывающий список символов алгебры». Математическое хранилище. 2020-03-25. Получено 2020-08-26.
2. Вайсштейн, Эрик В. «Вычитание». mathworld.wolfram.com. Получено 2020-08-26.
3. «Список арифметических и общих математических символов». Математическое хранилище. 2020-03-17. Получено 2020-08-26.
4. Шмид, Герман (1974). Десятичное вычисление (1-е изд.). Бингемтон, штат Нью-Йорк: Джон Уайли и сыновья. ISBN  978-0-471-76180-8.
5. Шмид, Герман (1983) [1974]. Десятичное вычисление (1 (переиздание) изд.). Малабар, Флорида: Издательская компания Роберта Кригера. ISBN  978-0-89874-318-0.
6. «Вычитание». www.mathsisfun.com. Получено 2020-08-26.
7. «Вычитание». Оксфордский словарь английского языка (Интернет-ред.). Издательство Оксфордского университета. (Подписка или членство участвующего учреждения требуется.)
8. Пол Э. Петерсон, Майкл Хендерсон, Мартин Р. Уэст (2014) Учителя против общества: что американцы думают о школах и как их исправить Издательство Brookings Institution Press, стр. 163
9. Джанет Колодзи (2006) Конвергентная журналистика: написание материалов и освещение в средствах массовой информации Rowman & Littlefield Publishers, стр. 180
10. Дэвид Гиллборн (2008) Расизм и образование: совпадение или заговор? Рутледж стр. 46
11. Пол Клэппер (1916). Обучение арифметике: Учебное пособие для учителей. стр.80 –. Получено 2016-03-11.
12. Сьюзан Росс и Мэри Пратт-Коттер. 2000. «Вычитание в Соединенных Штатах: историческая перспектива», Педагог математики 8 (1): 4–11. п. 8: «Эта новая версия алгоритма разложения [то есть с использованием костыля Браунелла] настолько доминирует в этой области, что сегодня [в Америке] редко можно встретить какой-либо другой алгоритм, используемый для обучения вычитанию».
13. Росс, Сьюзан С .; Пратт-Коттер, Мэри (1999). «Вычитание из исторической точки зрения». Школьные науки и математика. 99 (7): 389–93.
14. Клаппер 1916, стр. 177–.
15. Дэвид Юджин Смит (1913). Обучение арифметике. Джинн. стр.77 –. Получено 2016-03-11.
16. Многочисленные способы арифметики в повседневной математике UCSMP В архиве 2014-02-25 в Wayback Machine Вычитание: торговля в первую очередь
17. Вычитание частичных разностей В архиве 2014-06-23 на Wayback Machine; Многочисленные способы арифметики в повседневной математике UCSMP В архиве 2014-02-25 в Wayback Machine Вычитание: частичные различия
18. Многочисленные способы арифметики в повседневной математике UCSMP В архиве 2014-02-25 в Wayback Machine Вычитание: подсчет
19. Многочисленные способы арифметики в повседневной математике UCSMP В архиве 2014-02-25 в Wayback Machine Вычитание: вычитание слева направо
20. Многочисленные способы арифметики в повседневной математике UCSMP Вычитание: одно и то же правило изменения

Библиография

• Браунелл, W.A. (1939). Обучение как реорганизация: экспериментальное исследование по арифметике для третьего класса, Duke University Press.
• Вычитание в Соединенных Штатах: историческая перспектива, Сьюзан Росс, Мэри Пратт-Коттер, Педагог математики, Vol. 8, No. 1 (оригинальная публикация) и Vol. 10, № 1 (оттиск.) PDF

внешняя ссылка

• «Вычитание», Энциклопедия математики, EMS Press, 2001 [1994]
• Рабочие листы для печати: Рабочие листы вычитания, Вычитание одной цифры, Вычитание двух цифр, Четырехзначное вычитание, и Дополнительные рабочие листы вычитания
• Игра на вычитание в завязать узел
• Вычитание на японских счетах выбран из Абак: Тайна бусины