Законы диффузии Фикса - Ficks laws of diffusion - Wikipedia

Для техники измерения сердечный выброс, видеть Принцип Фика.

Молекулярная диффузия с микроскопической и макроскопической точки зрения. Изначально есть растворенное вещество молекулы слева от барьера (фиолетовая линия) и ни одной справа. Барьер удаляется, и растворенное вещество диффундирует, заполняя весь контейнер. Вершина: Одиночная молекула движется беспорядочно. Середина: Чем больше молекул, тем четче прослеживается тенденция к тому, что растворенное вещество заполняет контейнер все более равномерно. Нижний: При огромном количестве молекул растворенного вещества случайность становится необнаружимой: растворенное вещество, кажется, плавно и систематически перемещается из областей с высокой концентрацией в области с низкой концентрацией. Этот плавный поток описывается законами Фика.

Законы диффузии Фика описывать распространение и были получены Адольф Фик в 1855 г.^[1] Их можно использовать для решения коэффициент диффузии, D. Первый закон Фика можно использовать для вывода его второго закона, который, в свою очередь, идентичен закону Фика. уравнение диффузии.

Процесс распространения, подчиняющийся Законы Фика называется нормальной диффузией или диффузией Фика; в противном случае это называется аномальная диффузия или нефиковская диффузия.

История

В 1855 году физиолог Адольф Фик впервые сообщил^[1] его теперь хорошо известные законы, управляющие переносом массы через диффузионные средства. Работа Фика была вдохновлена ​​более ранними экспериментами Томас Грэм, в котором не были предложены фундаментальные законы, которыми Фик прославился. Закон Фика аналогичен отношениям, обнаруженным в ту же эпоху другими выдающимися учеными: Закон Дарси (гидравлический поток), Закон Ома (зарядный транспорт), и Закон Фурье (теплопередача).

Эксперименты Фика (по образцу Грэма) касались измерения концентраций и потоков соли, диффундирующей между двумя резервуарами через водяные трубки. Примечательно, что работа Фика в первую очередь касалась диффузии в жидкостях, потому что в то время диффузия в твердых телах не считалась вообще возможной.^[2] Сегодня законы Фика составляют основу нашего понимания диффузии в твердых телах, жидкостях и газах (при отсутствии движения объемной жидкости в последних двух случаях). Когда процесс распространения нет следовать законам Фика (что происходит, среди прочего, в случаях диффузии через пористые среды и диффузии набухающих пенетрантов),^[3][4] это упоминается как нефикский.

Первый закон Фика

Первый закон Фика связывает диффузный поток градиенту концентрации. Он постулирует, что поток идет из областей с высокой концентрацией в области с низкой концентрацией, с величиной, которая пропорциональна градиенту концентрации (пространственная производная), или, упрощенно говоря, концепция, что растворенное вещество будет перемещаться из области высокой концентрации в область низкой концентрации через градиент концентрации. В одном (пространственном) измерении закон может быть записан в различных формах, где наиболее распространена форма (см.^[5][6]) находится в молярном основании:

${\displaystyle J=-D{\frac {d\varphi }{dx}}}$

куда

• J это диффузионный поток, из которых измерение является количество вещества на единицу площадь на единицу время. J измеряет количество вещества, которое будет протекать через единицу площади за единицу времени.
• D это коэффициент диффузии или же диффузионность. Его размерность - это площадь в единицу времени.
• φ (для идеальных смесей) - это концентрация, размерность которой - количество вещества в единице объема.
• Икс - позиция, размерность которой равна длине.

D пропорциональна квадрату скорости диффундирующих частиц, который зависит от температуры, вязкость жидкости и размер частиц в соответствии с Соотношение Стокса – Эйнштейна.. В разбавленных водных растворах коэффициенты диффузии большинства ионов близки и имеют значения, которые при комнатной температуре находятся в диапазоне (0.6–2)×10⁻⁹ м²/ с. Для биологических молекул коэффициенты диффузии обычно составляют от 10⁻¹¹ до 10⁻¹⁰ м²/ с.

В двух или более измерениях мы должны использовать ∇, то дель или же градиент оператор, который обобщает первую производную, получая

${\displaystyle \mathbf {J} =-D\nabla \varphi }$

куда J обозначает вектор диффузионного потока.

Движущей силой одномерной диффузии является величина −∂φ/∂Икс, который для идеальных смесей является градиентом концентрации.

Альтернативные формулировки первого закона

Другая форма первого закона - записать его с первичной переменной как массовая доля (у_я, например, в кг / кг), тогда уравнение меняется на:

${\displaystyle \mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla y_{i}}$

куда

• индекс я обозначает яй вид,
• J_я это вектор диффузионного потока из яй вид (например, в моль / м²-s),
• M_я это молярная масса из яй вид, и
• ρ это смесь плотность (например, в кг / м³).

Обратите внимание, что ${\displaystyle \rho }$ находится за пределами градиент оператор. Это потому что:

${\displaystyle y_{i}={\frac {\rho _{si}}{\rho }}}$

куда ρ_си парциальная плотность яй вид.

Помимо этого, в химических системах, отличных от идеальных растворов или смесей, движущей силой диффузии каждого вида является градиент химический потенциал этого вида. Тогда первый закон Фика (одномерный случай) можно записать

${\displaystyle J_{i}=-{\frac {Dc_{i}}{RT}}{\frac {\partial \mu _{i}}{\partial x}}}$

куда

• индекс я обозначает яй вид.
• c - концентрация (моль / м³).
• р это универсальная газовая постоянная (Дж / К / моль).
• Т - абсолютная температура (К).
• µ - химический потенциал (Дж / моль).

Движущая сила закона Фика может быть выражена как разница в летучести:

${\displaystyle J_{i}=-{\frac {D}{RT}}{\frac {\partial f_{i}}{\partial x}}}$

Летучесть ${\displaystyle f_{i}}$ имеет единицы Па. ${\displaystyle f_{i}}$ - парциальное давление компонента i в паре ${\displaystyle f_{i}^{G}}$ или жидкость ${\displaystyle f_{i}^{L}}$ фаза. При парожидкостном равновесии поток испарения равен нулю, поскольку ${\displaystyle f_{i}^{G}=f_{i}^{L}}$.

Вывод первого закона Фика для газов

Ниже приведены четыре варианта закона Фика для бинарных газовых смесей. Они предполагают: тепловая диффузия незначительна; сила тела на единицу массы одинакова для обоих видов; и либо давление постоянно, либо оба вещества имеют одинаковую молярную массу. В этих условиях Ref. ^[7] подробно показано, как уравнение диффузии из кинетическая теория газов сводится к этой версии закона Фика:

${\displaystyle \mathbf {V_{i}} =-D\nabla \ln y_{i}}$ ,

куда V_я - скорость диффузии частиц я. С точки зрения видового потока это

${\displaystyle \mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla y_{i}}$ .

Если, кроме того, ${\displaystyle \nabla \rho =0}$, это сводится к наиболее распространенной форме закона Фика,

${\displaystyle \mathbf {J_{i}} =-D\nabla \varphi }$ .

Если (вместо или в дополнение к ${\displaystyle \nabla \rho =0}$) оба вида имеют одинаковую молярную массу, закон Фика принимает вид

${\displaystyle \mathbf {J_{i}} =-{\frac {\rho D}{M_{i}}}\nabla x_{i}}$,

куда ${\displaystyle x_{i}}$ это мольная доля частиц я.

Второй закон Фика

Второй закон Фика предсказывает, как диффузия вызывает изменение концентрации во времени. Это уравнение в частных производных который в одном измерении гласит:

${\displaystyle {\frac {\partial \varphi }{\partial t}}=D\,{\frac {\partial ^{2}\varphi }{\partial x^{2}}}}$

куда

• ${\displaystyle \varphi }$ - концентрация в размерах [(количества вещества) длины⁻³], например моль / м³; ${\displaystyle \varphi }$ = ${\displaystyle \varphi }$(Икс,т) это функция, которая зависит от местоположения Икс и время т
• т время, пример s
• D - коэффициент диффузии размером [длина² время⁻¹], пример m²/ с
• Икс позиция [длина], например, м

В двух или более измерениях мы должны использовать Лапласиан Δ = ∇², которая обобщает вторую производную, получая уравнение

${\displaystyle {\frac {\partial \varphi }{\partial t}}=D\Delta \varphi }$

Второй закон Фика имеет ту же математическую форму, что и Уравнение тепла и это фундаментальное решение такой же, как Тепловое ядро, кроме коммутационной теплопроводности ${\displaystyle k}$ с коэффициентом диффузии ${\displaystyle D}$:

${\displaystyle \varphi (x,t)={\frac {1}{\sqrt {4\pi Dt}}}\exp \left(-{\frac {x^{2}}{4Dt}}\right).}$

Вывод второго закона Фика

Второй закон Фика можно вывести из первого закона Фика и сохранение массы при отсутствии каких-либо химических реакций:

${\displaystyle {\frac {\partial \varphi }{\partial t}}+{\frac {\partial }{\partial x}}J=0\Rightarrow {\frac {\partial \varphi }{\partial t}}-{\frac {\partial }{\partial x}}\left(D{\frac {\partial }{\partial x}}\varphi \right)\,=0}$

Полагая, что коэффициент диффузии D чтобы быть константой, можно поменять порядки дифференцирования и умножить на константу:

${\displaystyle {\frac {\partial }{\partial x}}\left(D{\frac {\partial }{\partial x}}\varphi \right)=D{\frac {\partial }{\partial x}}{\frac {\partial }{\partial x}}\varphi =D{\frac {\partial ^{2}\varphi }{\partial x^{2}}}}$

и, таким образом, получают форму уравнений Фика, как было указано выше.

Для случая диффузии в двух или более измерениях второй закон Фика принимает вид

${\displaystyle {\frac {\partial \varphi }{\partial t}}=D\nabla ^{2}\varphi ,}$

что аналогично уравнение теплопроводности.

Если коэффициент диффузии не постоянный, а зависит от координаты или концентрации, второй закон Фика дает

${\displaystyle {\frac {\partial \varphi }{\partial t}}=\nabla \cdot (D\nabla \varphi ).}$

Важным примером является случай, когда φ находится в установившемся состоянии, то есть концентрация не меняется со временем, так что левая часть приведенного выше уравнения тождественно равна нулю. В одном измерении с постоянным D, решением для концентрации будет линейное изменение концентраций вдоль Икс. В двух или более измерениях мы получаем

${\displaystyle \nabla ^{2}\varphi =0}$

который Уравнение Лапласа, решения которых математики называют гармонические функции.

Примеры решений и обобщение

Второй закон Фика - частный случай уравнение конвекции-диффузии в котором нет адвективный поток и нет чистого объемного источника. Его можно вывести из уравнение неразрывности:

${\displaystyle {\frac {\partial \varphi }{\partial t}}+\nabla \cdot \mathbf {j} =R,}$

куда j это общая поток и р является чистым источником объема для φ. Предполагается, что единственным источником потока в этой ситуации является диффузный поток:

${\displaystyle \mathbf {j} _{\text{diffusion}}=-D\nabla \varphi }$

Подставляя определение диффузного потока в уравнение неразрывности и предполагая, что источника нет (р = 0), приходим ко второму закону Фика:

${\displaystyle {\frac {\partial \varphi }{\partial t}}=D{\frac {\partial ^{2}\varphi }{\partial x^{2}}}}$

Если бы поток был результатом обоих диффузионный поток и адвективный поток, то уравнение конвекции-диффузии это результат.

Пример решения 1: источник постоянной концентрации и длина диффузии

Простой случай диффузии со временем т в одном измерении (взятом как Икс-axis) от границы, расположенной в позиции Икс = 0, где концентрация поддерживается на уровне п₀ является

${\displaystyle n\left(x,t\right)=n_{0}\mathrm {erfc} \left({\frac {x}{2{\sqrt {Dt}}}}\right)}$.

куда erfc является дополнительным функция ошибки. Это тот случай, когда коррозионные газы диффундируют через окислительный слой к поверхности металла (если предположить, что концентрация газов в окружающей среде постоянна, а диффузионное пространство, то есть слой продуктов коррозии, полубесконечный, начиная с 0 на поверхности и бесконечно глубоко распространяясь в материал). Если, в свою очередь, диффузионное пространство бесконечный (длится как через слой с п(Икс,0) = 0, Икс > 0 и это с п(Икс,0) = п₀, Икс ≤ 0), то в решение вносятся поправки только с коэффициентом 1/2 перед п₀ (поскольку теперь диффузия происходит в обоих направлениях). Этот случай справедлив, когда некоторый раствор с концентрацией п₀ контактирует со слоем чистого растворителя. (Бокштейн, 2005) Длина 2√Dt называется длина диффузии и обеспечивает меру того, как далеко распространилась концентрация в Икс-направление диффузией во времени т (Птица, 1976).

В качестве быстрого приближения функции ошибок можно использовать первые 2 члена ряда Тейлора:

${\displaystyle n\left(x,t\right)=n_{0}\left[1-2\left({\frac {x}{2{\sqrt {Dt\pi }}}}\right)\right]}$

Если D зависит от времени, длина диффузии становится

${\displaystyle 2{\sqrt {\int _{0}^{t}D\tau \,d\tau }}.}$.

Эта идея полезна для оценки длины диффузии в цикле нагрева и охлаждения, где D зависит от температуры.

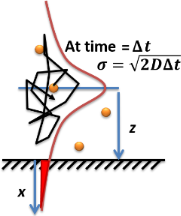
Пример решения 2: броуновская частица и среднеквадратичное смещение

Другой простой случай диффузии - это Броуновское движение одной частицы. Частицы Среднеквадратичное смещение от исходного положения:

${\displaystyle {\text{MSD}}\equiv \langle (\mathbf {x} -\mathbf {x_{0}} )^{2}\rangle =2nDt}$

куда ${\displaystyle n}$ это измерение броуновского движения частицы. Например, диффузия молекулы через клеточная мембрана Толщина 8 нм - одномерная диффузия из-за сферической симметрии; Однако диффузия молекулы от мембраны к центру эукариотическая клетка представляет собой трехмерную диффузию. Для цилиндрического кактус, диффузия от фотосинтетических клеток на его поверхности к его центру (оси его цилиндрической симметрии) является двумерной диффузией.

Квадратный корень из MSD, ${\displaystyle {\sqrt {2nDt}}}$, часто используется как характеристика того, как далеко переместилась частица с течением времени. ${\displaystyle t}$ истекло. МСД симметрично распределен в одномерном, двухмерном и трехмерном пространстве. Таким образом, распределение вероятностей величины СКО в 1D является гауссовым, а в 3D - распределением Максвелла-Больцмана.

Обобщения

• В неоднородные средыкоэффициент диффузии меняется в пространстве, D = D(Икс). Эта зависимость не влияет на первый закон Фика, но меняется второй закон:

${\displaystyle {\frac {\partial \varphi (x,t)}{\partial t}}=\nabla \cdot {\bigl (}D(x)\nabla \varphi (x,t){\bigr )}=D(x)\Delta \varphi (x,t)+\sum _{i=1}^{3}{\frac {\partial D(x)}{\partial x_{i}}}{\frac {\partial \varphi (x,t)}{\partial x_{i}}}}$

• В анизотропный средства массовой информациикоэффициент диффузии зависит от направления. Это симметричный тензор D = D_ij. Первый закон Фика меняется на

${\displaystyle J=-D\nabla \varphi }$,

это произведение тензора и вектора:

${\displaystyle J_{i}=-\sum _{j=1}^{3}D_{ij}{\frac {\partial \varphi }{\partial x_{j}}}.}$

Для уравнения диффузии эта формула дает

${\displaystyle {\frac {\partial \varphi (x,t)}{\partial t}}=\nabla \cdot {\bigl (}D\nabla \varphi (x,t){\bigr )}=\sum _{i=1}^{3}\sum _{j=1}^{3}D_{ij}{\frac {\partial ^{2}\varphi (x,t)}{\partial x_{i}\partial x_{j}}}.}$

Симметричная матрица коэффициентов диффузии D_ij должно быть положительно определенный. Это нужно, чтобы оператор правой стороны эллиптический.

• За неоднородные анизотропные среды эти две формы уравнения диффузии следует объединить в

${\displaystyle {\frac {\partial \varphi (x,t)}{\partial t}}=\nabla \cdot {\bigl (}D(x)\nabla \varphi (x,t){\bigr )}=\sum _{i,j=1}^{3}\left(D_{ij}(x){\frac {\partial ^{2}\varphi (x,t)}{\partial x_{i}\partial x_{j}}}+{\frac {\partial D_{ij}(x)}{\partial x_{i}}}{\frac {\partial \varphi (x,t)}{\partial x_{i}}}\right).}$

• Подход, основанный на Подвижность Эйнштейна и формула Теорелла дает следующее обобщение уравнения Фика для многокомпонентная диффузия из идеальных компонентов:

${\displaystyle {\frac {\partial \varphi _{i}}{\partial t}}=\sum _{j}\nabla \cdot \left(D_{ij}{\frac {\varphi _{i}}{\varphi _{j}}}\nabla \,\varphi _{j}\right).}$

куда φ_я - концентрации компонентов и D_ij - матрица коэффициентов. Здесь индексы я и j связаны с различными компонентами, а не с пространственными координатами.

В Формулы Чепмена – Энскога для диффузии в газах. включать точно такие же условия. Эти физические модели диффузии отличаются от тестовых моделей. ∂_тφ_я = ∑_j D_ij Δφ_j которые справедливы при очень малых отклонениях от однородного равновесия. Ранее такие термины были введены в Диффузия Максвелла – Стефана уравнение.

Для анизотропных многокомпонентных коэффициентов диффузии необходим тензор четвертого ранга, например D_ij,αβ, куда я, j обратитесь к компонентам и α, β = 1, 2, 3 соответствуют пространственным координатам.

Приложения

Уравнения, основанные на законе Фика, обычно использовались для моделирования транспортные процессы в продуктах питания, нейроны, биополимеры, фармацевтические препараты, пористый почвы, динамика населения, ядерные материалы, физика плазмы, и легирование полупроводников процессы. Теория всего вольтамперометрический метод основан на решениях уравнения Фика. Много экспериментальных исследований в полимер наука и наука о продуктах питания показали, что требуется более общий подход для описания переноса компонентов в материалах, подвергающихся стеклование. Вблизи стеклования поведение потока становится «нефиковым». Можно показать, что закон Фика можно получить из Диффузия Максвелла – Стефана уравнения Тейлор, Росс; Кришна, Р. (1993). «Многокомпонентный массообмен». Вайли. из многокомпонентный массообмен. Закон Фика является предельным случаем уравнений Максвелла-Стефана, когда смесь чрезвычайно разбавлена, и каждый химический компонент взаимодействует только с объемной смесью, а не с другими частицами. Чтобы учесть присутствие нескольких разновидностей в неразбавленной смеси, используются несколько вариаций уравнений Максвелла – Стефана. См. Также недиагональные связанные транспортные процессы (Онсагер отношение).

Течение Фика в жидкостях

Когда два смешивающийся жидкости вступают в контакт, и происходит диффузия, макроскопическая (или средняя) концентрация изменяется в соответствии с законом Фика. В мезоскопическом масштабе, то есть между макроскопическим масштабом, описываемым законом Фика, и молекулярным масштабом, где молекулярный случайные прогулки имеют место, нельзя пренебрегать колебаниями. Такие ситуации можно успешно моделировать с помощью флуктуирующей гидродинамики Ландау-Лифшица. В этой теоретической схеме диффузия обусловлена ​​флуктуациями, размеры которых варьируются от молекулярного до макроскопического масштаба.^[8]

В частности, уравнения флуктуирующей гидродинамики включают член Фика с заданным коэффициентом диффузии, а также уравнения гидродинамики и стохастические члены, описывающие флуктуации. При вычислении флуктуаций пертурбативным подходом приближение нулевого порядка является законом Фика. Первый порядок дает флуктуации, и получается, что флуктуации вносят вклад в диффузию. Это как-то представляет собой тавтология, поскольку явления, описываемые более низким приближением, являются результатом более высокого приближения: эта проблема решается только перенормировка уравнения флуктуирующей гидродинамики.

Скорость сорбции и частота столкновений разбавленных растворенных веществ

В адсорбция или же поглощение Скорость попадания разбавленного растворенного вещества на поверхность или границу раздела в растворе (газе или жидкости) может быть рассчитана с использованием законов диффузии Фика. Накопленное количество молекул, адсорбированных на поверхности, выражается уравнением Ленгмюра-Шефера на кратковременном пределе путем интегрирования уравнения диффузии по времени:^[9]

${\displaystyle \Gamma =2AC{\sqrt {\frac {Dt}{\pi }}}}$

Уравнение Ленгмюра-Шефера расширяется до уравнения Уорда-Тордай, чтобы учесть обратную диффузию отклоненных молекул с поверхности в более поздний момент адсорбции:^[10]

${\displaystyle \Gamma =2AC{\sqrt {\frac {Dt}{\pi }}}-A{\sqrt {\frac {D}{\pi }}}\int _{0}^{\sqrt {t}}{\frac {Cb(\tau )}{\sqrt {t-\tau }}}d\tau }$

куда C объемная концентрация, Cb - подповерхностная концентрация, которая является функцией времени, зависящей от модели реакции адсорбции, и τ - фиктивная переменная.

Квадратный корень (т) в зависимости от адсорбции, потому что, когда молекулы адсорбируются, концентрация в подповерхностных слоях падает и создает градиент концентрации у поверхности, который замедляет поглощение с течением времени. Это предположение можно подтвердить с помощью моделирования Монте-Карло.^[11]

Уравнение Ленгмюра-Шефера также может быть получено из анализа диффузии одиночных молекул. Учитывая одно измерение, перпендикулярное поверхности, вероятность того, что любая данная молекула растворенного вещества в растворе ударится о поверхность, равна функция ошибки диффузного расширения за интересующее время. Таким образом, интегрирование этих функций ошибок и интегрирование их со всеми молекулами растворенного вещества в объеме дает скорость адсорбции растворенного вещества в единицах s⁻¹ в интересующую область:^[12][11]

Схема молекулярной диффузии в растворе. Оранжевые точки - это молекулы растворенного вещества, молекулы растворителя не нарисованы, черная стрелка - это пример траектории случайного блуждания, а красная кривая - функция вероятности диффузионного гауссовского уширения из закона диффузии Фика.^{[12] Рис.9}

${\displaystyle r={\frac {1}{t}}\left(\int _{z=0}^{\infty }AC{\int _{x=z}^{\infty }{\frac {1}{\sqrt {4\pi Dt}}}e^{-{\frac {x^{2}}{4Dt}}}dx}dz\right)=AC{\sqrt {\frac {D}{\pi t}}}}$

куда

• Икс - это расстояние функции вероятности от исходного местоположения молекулы растворенного вещества (местоположение времени t относится к ее местоположению в момент времени 0, ${\displaystyle \Delta t=t-0}$)
• z - исходное расстояние молекулы от поверхности.
• А - площадь интересующей поверхности.
• C - числовая концентрация молекулы в объеме раствора.
• D - эффективная константа диффузии молекулы растворенного вещества, измеренная с разрешением по времени т.
• т это интересное время. Из-за негауссова хвоста типичной диффузионной системы т следует выбрать такое значение, чтобы р ≈ 1/т чтобы отразить основной эффект гауссова пика, т.е. около время первого прохождения т ≈ π/(4 D C ^2/3).^[11]
• Примечание: (1) D зависит от т, и функция вероятности обычно не гауссова. (2) Трехмерное решение удара небольшой (по сравнению с длиной диффузии) области на поверхности такое же, как и одномерное решение, только с использованием относительного аргумента, чтобы представить, что шар диффундирует в половину сферы по радиальному функция плотности вероятности из Распределение Максвелла – Больцмана.

В ультракоротком временном интервале, по порядку времени диффузии а²/D, куда а - радиус частицы, диффузия описывается Уравнение Ланжевена. В более длительное время Уравнение Ланжевена сливается с Уравнение Стокса – Эйнштейна.. Последнее подходит для состояния разбавленного раствора, в котором рассматривается дальняя диффузия. Согласно теорема флуктуации-диссипации на основе Уравнение Ланжевена в долговременном пределе и когда частица значительно плотнее окружающей жидкости, зависящая от времени константа диффузии равна:^[13]

${\displaystyle D(t)=\mu \,k_{\rm {B}}T(1-e^{-t/(m\mu )})}$

куда

• k_B является Постоянная Больцмана;
• Т это абсолютная температура.
• μ - подвижность частицы в жидкости или газе, которую можно рассчитать с помощью Соотношение Эйнштейна (кинетическая теория).
• м - масса частицы.
• т время.

Для отдельной молекулы, такой как органические молекулы или биомолекулы (например, белки) в воде, экспоненциальный член пренебрежимо мал из-за небольшого продукта mμ в пикосекундной области.

Когда интересующая область размером с молекулу (в частности, длинная цилиндрическая молекула например, ДНК), уравнение скорости адсорбции представляет собой частоту столкновения двух молекул в разбавленном растворе, при этом одна молекула находится на определенной стороне, а другая не имеет стерической зависимости, то есть молекула (случайная ориентация) сталкивается с одной стороной другой. Константу диффузии необходимо обновить до относительной постоянной диффузии между двумя диффундирующими молекулами. Эта оценка особенно полезна при изучении взаимодействия между небольшой молекулой и более крупной молекулой, такой как белок. В эффективной константе диффузии преобладает меньшая, вместо нее можно использовать константу диффузии.

Вышеприведенное уравнение скорости попадания также полезно для прогнозирования кинетики молекулярного самосборка на поверхности. В объемном растворе молекулы ориентированы случайным образом. Предполагая, что 1/6 молекул имеет правильную ориентацию по отношению к участкам связывания на поверхности, то есть 1/2 направления z в трех измерениях x, y, z, таким образом, интересующая концентрация составляет всего 1/6 от общей концентрации. Поместив это значение в уравнение, вы сможете рассчитать теоретическую кинетическую кривую адсорбции, используя Модель адсорбции Ленгмюра. В более жесткой картине 1/6 можно заменить стерическим фактором геометрии привязки.

Биологическая перспектива

Из первого закона возникает следующая формула:^[14]

${\displaystyle {\text{flux}}={-P\left(c_{2}-c_{1}\right)}}$

в котором,

• п проницаемость, экспериментально определенная мембрана "проводимость «для данного газа при данной температуре.
• c₂ − c₁ разница в концентрация газа через мембрана для направления потока (от c₁ к c₂).

Первый закон Фика также важен для уравнений переноса излучения. Однако в этом контексте это становится неточным, когда постоянная диффузии мала, и излучение ограничивается скоростью света, а не сопротивлением материала, через который проходит излучение. В этой ситуации можно использовать ограничитель потока.

Скорость обмена газа через жидкую мембрану можно определить, используя этот закон вместе с Закон Грэма.

В условиях разбавленного раствора, когда диффузия берет на себя управление, проницаемость мембраны, упомянутая в предыдущем разделе, может быть теоретически рассчитана для растворенного вещества с использованием уравнения, упомянутого в последнем разделе (используйте с особой осторожностью, поскольку уравнение выводится для плотных растворенных веществ, в то время как биологические молекулы не плотнее воды):^[12]

${\displaystyle P=2A_{p}\eta _{tm}{\sqrt {D/(\pi t)}}}$

куда

• ${\displaystyle A_{P}}$ - общая площадь пор на мембране (ед. м²).
• ${\displaystyle \eta _{tm}}$ трансмембранный КПД (безразмерный), который можно рассчитать по стохастической теории хроматография.
• D - постоянная диффузии растворенного вещества m²s⁻¹.
• т это единица времени с.
• c₂, c₁ концентрация должна использовать единицу моль м⁻³, поэтому единица потока становится моль с⁻¹.

Приложения для производства полупроводников

Интегральная схема технологии производства, модельные процессы, такие как химическое осаждение из паровой фазы, термическое окисление, влажное окисление, легирование и т. д., используют уравнения диффузии, полученные из закона Фика.

В некоторых случаях решения получены для граничных условий, таких как диффузия с постоянной концентрацией источника, ограниченная концентрация источника или диффузия по движущейся границе (когда глубина перехода продолжает перемещаться в подложку).

Смотрите также

• Распространение
• Осмос
• Поток массы
• Диффузия Максвелла – Стефана
• Уравнение Черчилля – Бернштейна
• Уравнение Нернста – Планка
• Газообмен
• Ложная диффузия
• Адвекция

Примечания

1. *Фик, А. (1855). «Ueber Diffusion». Annalen der Physik (на немецком). 94 (1): 59–86. Bibcode:1855AnP ... 170 ... 59F. Дои:10.1002 / andp.18551700105.
   • Фик, А. (1855). "V. О диффузии жидкости". Фил. Mag. 10 (63): 30–39. Дои:10.1080/14786445508641925.
2. Филибер, Жан (2005). «Полтора века распространения: Фик, Эйнштейн, до и после» (PDF). Основы диффузии. 2: 1.1–1.10. Архивировано из оригинал (PDF) 5 февраля 2009 г.
3. Васкес, Х. Л. (2006). «Уравнение пористой среды». Математическая теория. Oxford Univ. Нажмите.
4. Горбань, А.; Саргсян, Х.П .; Вахаб, Х.А. (2011). «Квазихимические модели многокомпонентной нелинейной диффузии». Математическое моделирование природных явлений. 6 (5): 184–262. arXiv:1012.2908. Дои:10.1051 / mmnp / 20116509. S2CID  18961678.
5. Аткинс, Питер; де Паула, Хулио (2006). Физическая химия для наук о жизни.
6. Конлиск, А. Терренс (2013). Основы микро- и нанофлюидики: с приложениями к биологическим и химическим наукам. Издательство Кембриджского университета. п. 43. ISBN  9780521881685.
7. Уильямс, Ф.А. (1985). «Приложение Е». Теория горения. Бенджамин / Каммингс.
8. Brogioli, D .; Вайлати, А. (2001). "Диффузионный массоперенос неравновесными колебаниями: пересмотр закона Фика". Phys. Ред. E. 63 (1–4): 012105. arXiv:cond-mat / 0006163. Bibcode:2001PhRvE..63a2105B. Дои:10.1103 / PhysRevE.63.012105. PMID  11304296. S2CID  1302913.
9. Langmuir, I .; Шефер, В. (1937). «Влияние растворенных солей на нерастворимые монослои». Журнал Американского химического общества. 29 (11): 2400–2414. Дои:10.1021 / ja01290a091.
10. Ward, A.F.H .; Тордай, Л. (1946). «Временная зависимость граничных напряжений решений I. Роль диффузии во временных эффектах». Журнал химической физики. 14 (7): 453–461. Дои:10.1063/1.1724167.
11. Чен, Дж. (2020). «Стохастическая адсорбция разбавленных молекул растворенного вещества на границах раздела». ChemRxiv. Дои:10.26434 / chemrxiv.12402404.v2.
12. Пайл, Джозеф Р .; Чен, Цзисинь (2 ноября 2017 г.). «Фотообесцвечивание YOYO-1 при визуализации флуоресценции одиночной ДНК со сверхвысоким разрешением». Журнал нанотехнологий Beilstein. 8: 2292–2306. Дои:10.3762 / bjnano.8.229. ЧВК  5687005. PMID  29181286.
13. Бянь, Синь; Ким, Чанхо; Карниадакис, Джордж Эм (14 августа 2016 г.). «111 лет броуновского движения». Мягкая материя. 12 (30): 6331–6346. Bibcode:2016SMat ... 12.6331B. Дои:10.1039 / c6sm01153e. ЧВК  5476231. PMID  27396746.
14. Носек, Томас М. "Раздел 3 / 3ч9 / с3ч9_2". Основы физиологии человека. Архивировано из оригинал 24 марта 2016 г.

Рекомендации

• Смит, В. Ф. (2004). Основы материаловедения и инженерии (3-е изд.). Макгроу-Хилл.
• Берг, Х.С. (1977). Случайные блуждания в биологии. Принстон.
• Bird, R. B .; Стюарт, W. E .; Лайтфут, Э. Н. (1976). Транспортные явления. Джон Вили и сыновья.
• Крэнк, Дж. (1980). Математика диффузии. Издательство Оксфордского университета.
• Бокштейн, Б. С .; Менделев, М. И .; Сроловиц, Д. Дж., Ред. (2005). Термодинамика и кинетика в материаловедении: краткий курс. Оксфорд: Издательство Оксфордского университета. стр.167 –171.
• Фик, А. (1855). «О жидкостной диффузии». Annalen der Physik und Chemie. 94: 59. - перепечатано в Фик, Адольф (1995). «О жидкостной диффузии». Журнал мембрановедения. 100: 33–38. Дои:10.1016 / 0376-7388 (94) 00230-в.

внешняя ссылка

• Уравнения Фика, преобразование Больцмана и др. (с фигурами и анимацией)
• Второй закон Фика на OpenStax