Ректифицированный 24-элементный - Rectified 24-cell
| Ректифицированный 24-элементный | ||
 Диаграмма Шлегеля Показано 8 из 24 кубооктаэдрических ячеек | ||
| Тип | Равномерный 4-многогранник | |
| Символы Шлефли | г {3,4,3} = rr {3,3,4} = г {31,1,1} = | |
| Диаграммы Кокстера | ||
| Клетки | 48 | 24 3.4.3.4 24 4.4.4 |
| Лица | 240 | 96 {3} 144 {4} |
| Края | 288 | |
| Вершины | 96 | |
| Фигура вершины |    Треугольная призма | |
| Группы симметрии | F4 [3,4,3], заказ 1152 B4 [3,3,4], заказ 384 D4 [31,1,1], заказ 192 | |
| Характеристики | выпуклый, реберно-транзитивный | |
| Единый индекс | 22 23 24 | |
В геометрия, то выпрямленный 24-элементный или же ректификованный икозитетрахорон - равномерный 4-мерный многогранник (или равномерный 4-многогранник ), что ограничено 48 клетки: 24 кубики, и 24 кубооктаэдр. Его можно получить исправление 24-ячейки, уменьшив ее октаэдрические ячейки до кубов и кубооктаэдров.[1]
Э. Л. Элте идентифицировал его в 1912 году как полуправильный многогранник, обозначив его как tC24.
Это также можно считать скошенный 16-элементный с низшими симметриями B4 = [3,3,4]. B4 приведет к двухцветному кубооктаэдр ячеек на 8 и 16 каждая. Его также называют рунический димитессеракт в рекламе4 симметрия, дающая 3 цвета ячеек, по 8 на каждую.
Строительство
Выпрямленный 24-элементный может быть получен из 24-элементного процесса исправление: 24 ячейки усекаются в середине. Вершины становятся кубики, в то время как октаэдры становиться кубооктаэдр.
Декартовы координаты
Выпрямленный 24-элементный с длиной ребра √2 имеет вершины, заданные всеми перестановками и перестановками знаков следующих Декартовы координаты:
- (0,1,1,2) [4!/2!×23 = 96 вершин]
Двойная конфигурация с длиной ребра 2 имеет все перестановки координат и знаков:
- (0,2,2,2) [4×23 = 32 вершины]
- (1,1,1,3) [4×24 = 64 вершины]
Изображений
| Самолет Кокстера | F4 | |
|---|---|---|
| График |  | |
| Двугранная симметрия | [12] | |
| Самолет Кокстера | B3 / А2 (а) | B3 / А2 (б) |
| График | 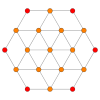 | 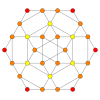 |
| Двугранная симметрия | [6] | [6] |
| Самолет Кокстера | B4 | B2 / А3 |
| График |  |  |
| Двугранная симметрия | [8] | [4] |
| Стереографическая проекция | |
|---|---|
 | |
| Центр стереографическая проекция с 96 треугольными гранями синий | |
Построения симметрии
Есть три различных конструкции симметрии этого многогранника. Нижайший строительство может быть удвоено в путем добавления зеркала, которое отображает разветвляющиеся узлы друг на друга. может быть сопоставлен с симметрия путем добавления двух зеркал, которые отображают все три конечных узла вместе.
В вершина фигура это треугольная призма, содержащий два куба и три кубооктаэдра. Три симметрии можно увидеть с 3 цветными кубооктаэдрами в самом нижнем конструкции и два цвета (соотношение 1: 2) в , и все одинаковые кубооктаэдры в .
| Группа Коксетера | = [3,4,3] | = [4,3,3] | = [3,31,1] |
|---|---|---|---|
| Заказ | 1152 | 384 | 192 |
| Полный симметрия группа | [3,4,3] | [4,3,3] | <[3,31,1]> = [4,3,3] [3[31,1,1]] = [3,4,3] |
| Диаграмма Кокстера | |||
| Грани | 3: 2: | 2,2: 2: | 1,1,1: 2: |
| Фигура вершины |  |  |  |
Альтернативные имена
- Выпрямленный 24-элементный, складчатый 16-элементный (Норман Джонсон )
- Ректифицированный икозитетрахорон (Acronym rico) (Джордж Ольшевский, Джонатан Бауэрс)
- Кантеллированный гексадекахорон
- Дисикоситетрахорон
- Амбоикоситетрахорон (Нил Слоан и Джон Хортон Конвей )
Связанные многогранники
Выпуклая оболочка выпрямленной 24-клеточной и двойственной к ней (в предположении, что они конгруэнтны) представляет собой неоднородный полихорон, состоящий из 192 клеток: 48 кубики, 144 квадратные антипризмы, и 192 вершины. Его вершина - фигура треугольный двустворчатый.
Связанные однородные многогранники
| D4 однородная полихора | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  | ||||
| {3,31,1} ч {4,3,3} | 2r {3,31,1} час3{4,3,3} | т {3,31,1} час2{4,3,3} | 2т {3,31,1} час2,3{4,3,3} | г {3,31,1} {31,1,1}={3,4,3} | рр {3,31,1} г {31,1,1} = г {3,4,3} | tr {3,31,1} т {31,1,1} = t {3,4,3} | sr {3,31,1} с {31,1,1} = s {3,4,3} | ||||
| Семейные многогранники из 24 клеток | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | 24-элементный | усеченный 24-элементный | курносый 24-элементный | выпрямленный 24-элементный | наклонный 24-элементный | усеченный битами 24 ячейки | усеченный 24-элементный | беглый 24-элементный | усеченный 24-элементный | комплексно усеченные 24 ячейки | |
| Schläfli символ | {3,4,3} | т0,1{3,4,3} т {3,4,3} | с {3,4,3} | т1{3,4,3} г {3,4,3} | т0,2{3,4,3} рр {3,4,3} | т1,2{3,4,3} 2т {3,4,3} | т0,1,2{3,4,3} tr {3,4,3} | т0,3{3,4,3} | т0,1,3{3,4,3} | т0,1,2,3{3,4,3} | |
| Coxeter диаграмма | |||||||||||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  |  | |
| F4 |  |  |  |  |  |  |  |  |  |  | |
| B4 |  |  |  |  |  |  |  |  |  |  | |
| B3(а) |  |  |  |  |  |  |  |  |  |  | |
| B3(б) |  |  |  |  |  |  | |||||
| B2 |  |  |  |  |  |  |  |  |  |  | |
В выпрямленный 24-элементный также может быть получено как скошенный 16-элементный:
| Многогранники симметрии B4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | тессеракт | исправленный тессеракт | усеченный тессеракт | канеллированный тессеракт | разбитый тессеракт | усеченный битами тессеракт | усеченный тессеракт | runcitruncated тессеракт | всесторонне усеченный тессеракт | ||
| Coxeter диаграмма | = | = | |||||||||
| Schläfli символ | {4,3,3} | т1{4,3,3} г {4,3,3} | т0,1{4,3,3} т {4,3,3} | т0,2{4,3,3} рр {4,3,3} | т0,3{4,3,3} | т1,2{4,3,3} 2т {4,3,3} | т0,1,2{4,3,3} tr {4,3,3} | т0,1,3{4,3,3} | т0,1,2,3{4,3,3} | ||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
| Имя | 16 ячеек | исправленный 16 ячеек | усеченный 16 ячеек | канеллированный 16 ячеек | разбитый 16 ячеек | усеченный битами 16 ячеек | усеченный 16 ячеек | runcitruncated 16 ячеек | всесторонне усеченный 16 ячеек | ||
| Coxeter диаграмма | = | = | = | = | = | = | |||||
| Schläfli символ | {3,3,4} | т1{3,3,4} г {3,3,4} | т0,1{3,3,4} т {3,3,4} | т0,2{3,3,4} рр {3,3,4} | т0,3{3,3,4} | т1,2{3,3,4} 2т {3,3,4} | т0,1,2{3,3,4} tr {3,3,4} | т0,1,3{3,3,4} | т0,1,2,3{3,3,4} | ||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
Цитаты
- ^ Кокстер 1973, п. 154, §8.4.
Рекомендации
- Т. Госсет: О регулярных и полурегулярных фигурах в пространстве n измерений, Вестник математики, Macmillan, 1900 г.
- Кокстер, H.S.M. (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Дувр.CS1 maint: ref = harv (связь)
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. с. 409: Hemicubes: 1n1)
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. (1966)
- 2. Выпуклая однородная полихора на основе тессеракта (8-элементный) и гексадекахорон (16-элементный) - Модель 23., Георгий Ольшевский.
- 3. Выпуклая однородная полихора на основе икоситетрахорона (24-ячеечная) - Модель 23., Георгий Ольшевский.
- 7. Равномерная полихора, полученная из гломерного тетраэдра B4 - Модель 23., Георгий Ольшевский.
- Клитцинг, Ричард. "4D однородные многогранники (полихора) o3x4o3o - rico".







