Кантеллированный тессеракт - Cantellated tesseract
 тессеракт | 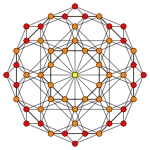 Кантеллированный тессеракт |  Собранный 16-элементный (Ректифицированный 24-элементный ) |
 16 ячеек |  Усеченный тессеракт |  Cantitruncated 16-элементный (Усеченный 24-элементный ) |
| Ортогональные проекции в4 Самолет Кокстера | ||
|---|---|---|
В четырехмерном геометрия, а скошенный тессеракт выпуклый равномерный 4-многогранник, быть песня (усечение 2-го порядка) регулярного тессеракт.
Существует четыре степени наклонов тессеракта, в том числе с усечением перестановок. Два также происходят из 24-клеточного семейства.
Кантеллированный тессеракт
| Кантеллированный тессеракт | ||
|---|---|---|
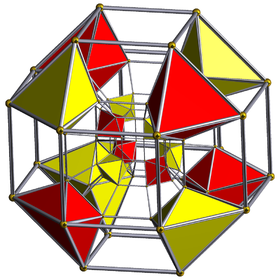 Диаграмма Шлегеля С центром на ромбокубооктаэдре показаны октаэдрические ячейки | ||
| Тип | Равномерный 4-многогранник | |
| Символ Шлефли | рр {4,3,3} | |
| Диаграмма Кокстера | ||
| Клетки | 56 | 8 3.4.4.4 16 3.3.3.3 32 3.4.4 |
| Лица | 248 | 128 {3} 120 {4} |
| Края | 288 | |
| Вершины | 96 | |
| Фигура вершины |  Квадратный клин | |
| Группа симметрии | B4, [3,3,4], заказ 384 | |
| Характеристики | выпуклый | |
| Единый индекс | 13 14 15 | |
В скошенный тессеракт, двухслойный 16-элементный, или же маленький ромбовидный тессеракт выпуклый равномерный 4-многогранник или 4-х мерный многогранник ограничен 56 клетки: 8 малые ромбокубооктаэдры, 16 октаэдры, и 32 треугольные призмы.
Строительство
В процессе песня, 2-грани многогранника эффективно сжимаются. В ромбокубооктаэдр можно назвать угловым кубом, поскольку если его шесть граней сжать в соответствующих плоскостях, каждая вершина разделится на три вершины треугольников ромбокубооктаэдра, а каждое ребро разделится на два из противоположных ребер ромбокубооктаэдров, двенадцать неосевых квадраты.
Когда тот же процесс применяется к тессеракту, каждый из восьми кубов становится ромбокубооктаэдром описанным образом. В дополнение, однако, поскольку ребро каждого куба ранее было общим с двумя другими кубами, разделяющие ребра образуют три параллельных ребра треугольной призмы - 32 треугольные призмы, поскольку было 32 ребра. Кроме того, поскольку каждая вершина ранее была разделена с тремя другими кубами, вершина будет разделена на 12, а не на три новые вершины. Однако, поскольку некоторые из усохших граней остаются общими, определенные пары из этих 12 потенциальных вершин идентичны друг другу, и поэтому только 6 новых вершин создаются из каждой исходной вершины (следовательно, 96 вершин скошенного тессеракта по сравнению с 16 вершинами тессеракта). ). Эти шесть новых вершин образуют вершины октаэдра - 16 октаэдров, поскольку тессеракт имел 16 вершин.
Декартовы координаты
В Декартовы координаты вершин скошенного тессеракта с длиной ребра 2 задается всеми перестановками:
Структура
8 маленьких ромбокубооктаэдрических ячеек соединены друг с другом их квадратными осевыми гранями. Их неосевые квадратные грани, соответствующие ребрам куба, соединены с треугольными призмами. Треугольные грани малых ромбокубооктаэдров и треугольных призм соединены с 16 октаэдрами.
Его структуру можно представить с помощью самого тессеракта: ромбокубооктаэдры аналогичны ячейкам тессеракта, треугольные призмы аналогичны ребрам тессеракта, а октаэдры аналогичны вершинам тессеракта.
Изображений
| Самолет Кокстера | B4 | B3 / D4 / А2 | B2 / D3 |
|---|---|---|---|
| График |  | 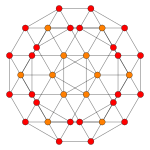 | 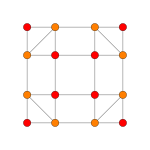 |
| Двугранная симметрия | [8] | [6] | [4] |
| Самолет Кокстера | F4 | А3 | |
| График |  |  | |
| Двугранная симметрия | [12/3] | [4] |
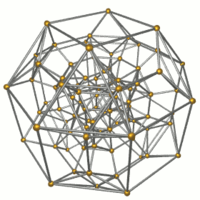 Каркас | 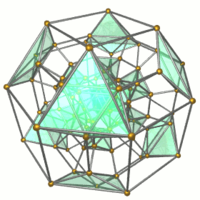 16 октаэдры показано. |  32 треугольные призмы показано. |
Прогнозы
Ниже показано расположение ячеек наклонного тессеракта в параллельной проекции в трехмерное пространство, сначала маленький ромбокубооктаэдр:
- Конверт проекции - это усеченный куб.
- Ближайшие и самые дальние маленькие ромбокубооктаэдрические ячейки с точки зрения 4D проектируются в объем той же формы, вписанный в конверт проекции.
- Осевые квадраты этого небольшого центрального ромбокубооктаэдра касаются центров шести восьмиугольников оболочки. Восьмиугольники - это изображение остальных 6 маленьких ромбокубооктаэдрических ячеек.
- 12 клиновидных объемов, соединяющих неосевые квадратные грани центрального малого ромбокубооктаэдра с соседними восьмиугольниками, являются изображениями 24 треугольных призм.
- Остальные 8 треугольных призм выступают на треугольные грани конверта.
- Между треугольными гранями оболочки и треугольными гранями центрального малого ромбокубооктаэдра расположены 8 октаэдрических объемов, которые являются изображениями 16 октаэдрических ячеек.
Такое расположение ячеек в проекции аналогично расположению лиц в проекции усеченный куб в 2 измерениях. Следовательно, косоугольный тессеракт можно рассматривать как аналог усеченного куба в четырех измерениях. (Это не единственный возможный аналог; другим близким кандидатом является усеченный тессеракт.)
Еще один равномерный 4-многогранник с аналогичным расположением ячеек - это усеченный 16-элементный.
Усеченный тессеракт
| Усеченный тессеракт | ||
 Диаграмма Шлегеля сосредоточен на усеченный кубооктаэдр ячейка с восьмиугольный лица скрыты. | ||
| Тип | Равномерный 4-многогранник | |
| Символ Шлефли | tr {4,3,3} | |
| Диаграммы Кокстера | ||
| Клетки | 56 | 8 4.6.8 16 3.6.6 32 3.4.4 |
| Лица | 248 | 64 {3} 96 {4} 64 {6} 24 {8} |
| Края | 384 | |
| Вершины | 192 | |
| Фигура вершины | 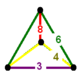 Клиновидная | |
| Группа симметрии | B4, [3,3,4], заказ 384 | |
| Характеристики | выпуклый | |
| Единый индекс | 17 18 19 | |
В геометрия, то усеченный тессеракт или же большой ромбовидный тессеракт это равномерный 4-многогранник (или равномерный 4-х мерный многогранник ), что ограничено 56 клетки: 8 усеченные кубооктаэдры, 16 усеченные тетраэдры, и 32 треугольные призмы.
Строительство
Обрезанный тессеракт создается путем усечения тессеракт Под сокращением часто понимают исправление с последующим усечением. Однако результатом этого построения был бы многогранник, который, хотя его структура была бы очень похожа на структуру, заданную с помощью усечения, не все его грани были бы однородными.
В качестве альтернативы униформа усеченный тессеракт можно построить, поместив 8 единообразных усеченные кубооктаэдры в гиперплоскостях ячеек тессеракта, смещенных по координатным осям так, чтобы их восьмиугольные грани совпадали. Для длины ребра 2 эта конструкция дает Декартовы координаты его вершин как все перестановки:
Структура
8 усеченных кубооктаэдров соединены друг с другом своими восьмиугольными гранями в расположении, соответствующем 8 кубическим ячейкам тессеракта. Они соединены с 16 усеченными тетраэдрами своими шестиугольными гранями, а их квадратные грани присоединены к квадратным граням 32 треугольных призм. Треугольные грани треугольных призм соединены с усеченными тетраэдрами.
Усеченные тетраэдры соответствуют вершинам тессеракта, а треугольные призмы соответствуют ребрам тессеракта.
Изображений
| Самолет Кокстера | B4 | B3 / D4 / А2 | B2 / D3 |
|---|---|---|---|
| График |  |  |  |
| Двугранная симметрия | [8] | [6] | [4] |
| Самолет Кокстера | F4 | А3 | |
| График |  |  | |
| Двугранная симметрия | [12/3] | [4] |
 А стереографическая проекция усеченного тессеракта, как мозаику на 3-сфера, с его 64 синими треугольниками, 96 зелеными квадратами и 64 красными шестиугольными гранями (восьмиугольные грани не нарисованы). |
Прогнозы
В первой параллельной проекции усеченного кубооктаэдра в 3 измерения ячейки наклонно усеченного тессеракта расположены следующим образом:
- Конверт проекции - неоднородный усеченный куб, с более длинными краями между восьмиугольниками и более короткими краями в 8 треугольниках.
- Неправильные восьмиугольные грани оболочки соответствуют изображениям 6 из 8 усеченных кубооктаэдрических ячеек.
- Две другие усеченные кубооктаэдрические ячейки выступают в усеченный кубооктаэдр, вписанный в конверт проекции. Восьмиугольные грани касаются неправильных восьмиугольников конверта.
- В пространствах, соответствующих граням куба, лежат 12 объемов в форме неправильных треугольных призм. Это изображения, по одному на пару, 24 ячеек треугольной призмы.
- Остальные 8 треугольных призм проецируются на треугольные грани конверта проекции.
- Остальные 8 пространств, соответствующих углам куба, представляют собой образы 16 усеченных тетраэдров, по паре на каждое пространство.
Это расположение ячеек в проекции похоже на раскладывающийся тессеракт.
Альтернативные названия
- Усеченный тессеракт (Норман В. Джонсон )
- Cantitruncated 4-куб
- Усеченный 8-элементный
- Гантусеченный октахорон
- Большой призматотессерактигексадекахорон (Георгий Ольшевский)
- Грит (Джонатан Бауэрс: для большого ромбовидного тессеракта)
- 012-амвонский тессеракт (Джон Конвей )
Связанные однородные многогранники
| Многогранники симметрии B4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | тессеракт | исправленный тессеракт | усеченный тессеракт | скошенный тессеракт | разбитый тессеракт | усеченный битами тессеракт | усеченный тессеракт | runcitruncated тессеракт | всесторонне усеченный тессеракт | ||
| Coxeter диаграмма | = | = | |||||||||
| Schläfli символ | {4,3,3} | т1{4,3,3} г {4,3,3} | т0,1{4,3,3} т {4,3,3} | т0,2{4,3,3} рр {4,3,3} | т0,3{4,3,3} | т1,2{4,3,3} 2т {4,3,3} | т0,1,2{4,3,3} tr {4,3,3} | т0,1,3{4,3,3} | т0,1,2,3{4,3,3} | ||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
| Имя | 16 ячеек | исправленный 16 ячеек | усеченный 16 ячеек | скошенный 16 ячеек | разбитый 16 ячеек | усеченный битами 16 ячеек | усеченный 16 ячеек | runcitruncated 16 ячеек | всесторонне усеченный 16 ячеек | ||
| Coxeter диаграмма | = | = | = | = | = | = | |||||
| Schläfli символ | {3,3,4} | т1{3,3,4} г {3,3,4} | т0,1{3,3,4} т {3,3,4} | т0,2{3,3,4} рр {3,3,4} | т0,3{3,3,4} | т1,2{3,3,4} 2т {3,3,4} | т0,1,2{3,3,4} tr {3,3,4} | т0,1,3{3,3,4} | т0,1,2,3{3,3,4} | ||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
Это второй в серии усеченных усеченных гиперкубов:
  |   |   |   |   |   |
| Усеченный кубооктаэдр | Усеченный тессеракт | Усеченный 5-куб | Усеченный 6-куб | Cantitruncated 7-куб | Усеченный 8-куб |
Рекомендации
- Т. Госсет: О регулярных и полурегулярных фигурах в пространстве n измерений, Вестник математики, Macmillan, 1900 г.
- H.S.M. Coxeter:
- Кокстер, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8, п. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерном пространстве (n≥5)
- H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973, стр. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерном пространстве (n≥5)
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. с. 409: Hemicubes: 1n1)
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. (1966)
- 2. Выпуклая однородная полихора на основе тессеракта (8-элементный) и гексадекахорон (16-элементный) - Модель 14, 18., Георгий Ольшевский.
- Клитцинг, Ричард. «4D однородные многогранники (полихоры)». o3x3o4x - зернистость, o3x3x4x - зернистость
- Бумажная модель усеченного тессеракта созданы с использованием сетей, созданных Stella4D программного обеспечения






