Распределение степеней - Degree distribution
| Сетевая наука | ||||
|---|---|---|---|---|
| Типы сетей | ||||
| Графики | ||||
| ||||
| Модели | ||||
| ||||
| ||||
| ||||
При изучении графики и сети, то степень узла в сети - это количество подключений, которые он имеет к другим узлам, а распределение степеней это распределение вероятностей этих степеней по всей сети.
Определение
В степень узла в сети (иногда неправильно называемый возможность подключения ) - количество подключений или края узел имеет к другим узлам. Если сеть направленный, что означает, что ребра указывают в одном направлении от одного узла к другому, тогда узлы имеют две разные степени: внутреннюю степень, которая представляет собой количество входящих ребер, и исходную степень, которая представляет собой количество исходящих ребер.
Распределение степеней п(k) сети определяется как доля узлов в сети со степенью k. Таким образом, если есть п узлов всего в сети и пk из них имеют степень k, у нас есть .
Эта же информация также иногда представлена в виде совокупное распределение степеней, доля узлов со степенью меньше k, или даже дополнительное распределение накопленных степеней, доля узлов со степенью больше или равной k (1 - C) если учесть C как совокупное распределение степеней; то есть дополнение C.
Наблюдаемое распределение степеней
Распределение степеней очень важно при изучении обеих реальных сетей, таких как Интернет и социальные сети, и теоретические сети. Простейшая сетевая модель, например (модель Эрдеша – Реньи) случайный граф, в котором каждый из п узлов независимо связаны (или нет) с вероятностью п (или 1 - п), имеет биномиальное распределение степеней k:
(или же Пуассон в пределе большого п, если средняя степень фиксируется). Однако в большинстве сетей в реальном мире распределение степеней сильно отличается от этого. Большинство очень наклоненный вправо, что означает, что подавляющее большинство узлов имеют низкую степень, но небольшое количество, известное как «концентраторы», имеет высокую степень. Некоторые сети, в частности Интернет, Всемирная паутина, и утверждалось, что в некоторых социальных сетях распределение степеней примерно соответствует сила закона: , куда γ является константой. Такие сети называются безмасштабные сети и привлекли особое внимание своими структурными и динамическими свойствами.[1][2][3][4] Однако в последнее время были проведены некоторые исследования, основанные на реальных наборах данных, которые утверждали, что, несмотря на то, что большинство наблюдаемых сетей имеют жирно-хвостовые степени распределения, они отклоняются от того, чтобы быть безмасштабный.[5]
Распределение избыточной степени
Распределение избыточной степени - это распределение вероятности для узла, достигаемого по ребру, числа других ребер, прикрепленных к этому узлу.[6] Другими словами, это распределение исходящих ссылок от узла, достигнутого при переходе по ссылке.
Предположим, что сеть имеет распределение степеней , выбрав один узел (случайно или нет) и перейдя к одному из его соседей (при условии, что у него есть хотя бы один сосед), то вероятность того, что этот узел будет иметь соседям не дается . Причина в том, что всякий раз, когда какой-либо узел выбирается в гетерогенной сети, более вероятно достичь хобов, следуя за одним из существующих соседей этого узла. Истинная вероятность того, что такие узлы имеют степень является который называется избыточная степень этого узла. в модель конфигурации, при котором корреляции между узлами были проигнорированы, и предполагается, что каждый узел связан с любыми другими узлами в сети с той же вероятностью, распределение избыточной степени может быть найдено как:[6]
куда это средний градус (средняя степень) модели. Из этого следует, что средняя степень соседа любого узла больше, чем средняя степень этого узла. В социальных сетях это означает, что у ваших друзей в среднем больше друзей, чем у вас. Это известно как парадокс дружбы. Можно показать, что сеть может иметь гигантский компонент, если его средняя степень превышения больше единицы:
Имейте в виду, что последние два уравнения предназначены только для модель конфигурации и чтобы получить избыточное распределение степеней сети реального слова, мы также должны учитывать корреляции степеней.[6]
Метод производящих функций
Производящие функции может использоваться для расчета различных свойств случайных сетей. Учитывая распределение степеней и избыточное распределение степеней некоторой сети, и соответственно, можно записать два степенных ряда в следующих формах:
и
также могут быть получены из производных :
Если мы знаем производящую функцию для распределения вероятностей тогда мы можем восстановить значения путем дифференцирования:
Некоторые свойства, например моменты, можно легко вычислить из и его производные:
И вообще:[6]
За Пуассон -распределенные случайные сети, такие как График ER, , поэтому теория случайных сетей этого типа особенно проста. Распределения вероятностей для 1-го и 2-го ближайших соседей генерируются функциями и . В более широком смысле, распределение -ые соседи генерируются:
, с итерации функции действует на себя.[7]
Среднее количество первых соседей, , является и среднее количество вторых соседей:
Распределение степеней для направленных сетей
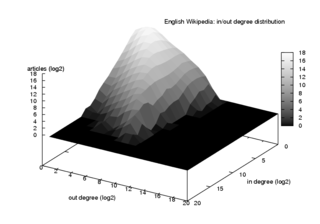
В направленной сети каждый узел имеет некоторую степень и некоторая степень которые представляют собой количество ссылок, которые должным образом входили и выходили из этого узла. Если вероятность того, что случайно выбранный узел имеет и диплом то производящая функция, присвоенная этому совместное распределение вероятностей можно записать двумя ценностями и в качестве:
Поскольку каждая ссылка в направленной сети должна покинуть один узел и войти в другой, чистое среднее количество входящих ссылок
узел равен нулю. Следовательно,
,
что означает, что функция генерации должна удовлетворять:
куда - средняя степень (как входящих, так и исходящих) узлов в сети;
Используя функцию , мы снова можем найти функцию генерации для распределения степени входа / выхода и распределения степени увеличения / выхода, как и раньше. может быть определена как производящая функция для числа входящих ссылок в случайно выбранном узле, и может быть определено как количество поступающих ссылок на узел, достигнутый путем перехода по случайно выбранной ссылке. Мы также можем определить производящие функции и для номера, выходящего из такого узла:[7]
Здесь среднее количество первых соседей, , или как ранее было введено как , является и среднее количество 2-х соседей, доступных из случайно выбранного узла, определяется как: . Это также номера 1-го и 2-го соседей, из которых может быть достигнут случайный узел, поскольку эти уравнения явно симметричны в и .[7]
Смотрите также
Рекомендации
- ^ Барабаши, Альберт-Ласло; Альберт, Река (1999-10-15). «Появление масштабирования в случайных сетях». Наука. 286 (5439): 509–512. arXiv:cond-mat / 9910332. Bibcode:1999Научный ... 286..509Б. Дои:10.1126 / science.286.5439.509. ISSN 0036-8075. PMID 10521342.
- ^ Альберт, Река; Барабаши, Альберт-Ласло (2000-12-11). «Топология развивающихся сетей: локальные события и универсальность» (PDF). Письма с физическими проверками. 85 (24): 5234–5237. arXiv:cond-mat / 0005085. Bibcode:2000ПхРвЛ..85.5234А. Дои:10.1103 / Physrevlett.85.5234. HDL:2047 / d20000695. ISSN 0031-9007. PMID 11102229.
- ^ Дороговцев, С. Н .; Mendes, J. F. F .; Самухин, А. Н. (21.05.2001). «Распределение степеней в зависимости от размера немасштабируемой растущей сети». Физический обзор E. 63 (6): 062101. arXiv:cond-mat / 0011115. Bibcode:2001PhRvE..63f2101D. Дои:10.1103 / Physreve.63.062101. ISSN 1063-651X. PMID 11415146.
- ^ Пахон, Анжелика; Сакердот, Лаура; Ян, Шуйи (2018). «Безмасштабное поведение сетей при одновременном наличии льготных и единых правил присоединения». Physica D: нелинейные явления. 371: 1–12. arXiv:1704.08597. Bibcode:2018PhyD..371 .... 1P. Дои:10.1016 / j.physd.2018.01.005.
- ^ Холм, Петтер (04.03.2019). "Редко и повсюду: перспективы безмасштабных сетей". Nature Communications. 10 (1): 1016. Bibcode:2019НатКо..10.1016H. Дои:10.1038 / s41467-019-09038-8. ISSN 2041-1723. ЧВК 6399274. PMID 30833568.
- ^ а б c d Ньюман, Марк (2018-10-18). Сети. 1. Издательство Оксфордского университета. Дои:10.1093 / осо / 9780198805090.001.0001. ISBN 978-0-19-880509-0.
- ^ а б c Newman, M. E. J .; Strogatz, S.H .; Уоттс, Д. Дж. (24 июля 2001 г.). «Случайные графы с произвольными распределениями степеней и их приложения». Физический обзор E. 64 (2): 026118. Дои:10.1103 / PhysRevE.64.026118. ISSN 1063-651X.
- Albert, R .; Барабаши, А.-Л. (2002). «Статистическая механика сложных сетей». Обзоры современной физики. 74 (1): 47–97. arXiv:cond-mat / 0106096. Bibcode:2002РвМП ... 74 ... 47А. Дои:10.1103 / RevModPhys.74.47.
- Дороговцев, С .; Мендес, Дж. Ф. Ф. (2002). «Эволюция сетей». Успехи в физике. 51 (4): 1079–1187. arXiv:cond-mat / 0106144. Bibcode:2002AdPhy..51.1079D. Дои:10.1080/00018730110112519.
- Ньюман, М. Э. Дж. (2003). «Структура и функции сложных сетей». SIAM Обзор. 45 (2): 167–256. arXiv:cond-mat / 0303516. Bibcode:2003SIAMR..45..167N. Дои:10.1137 / S003614450342480.
- Шломо Хавлин И Реувен Коэн (2010). Сложные сети: структура, надежность и функции. Издательство Кембриджского университета.




















![{ displaystyle { langle k ^ {m} rangle} = { Biggl [} {{ bigg (} operatorname {x} { operatorname {d} ! over operatorname {dx} !} { biggl)} ^ {m}} G_ {0} (x) { Biggl]} _ {x = 1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9906ae36afd8a3c61e56fec3a175c839b8206439)








![{ displaystyle c_ {2} = { biggl [} {d over dx} G_ {0} { big (} G_ {1} (x) { big)} { biggl]} _ {x = 1 } = G_ {1} '(1) G' _ {0} { big (} G_ {1} (1) { big)} = G_ {1} '(1) G' _ {0} (1 ) = G '' _ {0} (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a226661873e033c63285c727c723aa8422452ce)




















