Проблема минимального сопротивления Ньютона - Newtons minimal resistance problem - Wikipedia

Задача минимального сопротивления Ньютона проблема поиска твердое тело революции который испытывает минимальное сопротивление при движении через однородную жидкость с постоянной скоростью в направлении оси вращения, названной в честь Исаак Ньютон, который изучил проблему в 1685 г. и опубликовал ее в 1687 г. в своей Principia Mathematica.^{[1][страница нужна ]} Это первый пример проблемы, решенной в том, что сейчас называется вариационное исчисление, появившись за десять лет до проблема брахистохрона.^[2] Ньютон опубликовал решение в Principia Mathematica без его происхождения и Дэвид Грегори был первым, кто подошел к Ньютону и убедил его написать для него анализ. Затем Грегори поделился выводом со своими учениками и коллегами.^[3]

По словам Бернарда Коэна в своем «Путеводителе по принципам Ньютона», «ключ к рассуждениям Ньютона был найден в 1880-х годах, когда граф Портсмут передал Кембриджскому университету обширную коллекцию научных и математических работ Ньютона. Среди рукописей Ньютона они нашли черновой текст письма, ... в котором Ньютон развил свой математический аргумент. [Это] никогда не было полностью понято, однако, до публикации основных рукописных документов Д. Т. Уайтсайдом [1974], чьи аналитические и исторические комментарии позволили студентам Ньютону следует не только полностью следовать пути Ньютона к открытию и доказательству, но и повторному расчету поверхности наименьшего сопротивления, сделанному Ньютоном позднее (1694 г.) ».^[4][5]

Несмотря на то, что модель жидкости Ньютона была неправильной в соответствии с нашим текущим пониманием, жидкость, которую он рассматривал, находит свое применение в Гиперзвуковой поток теория как предельный случай.^[6]

Определение

В предложении 34 книги 2 Принципов Ньютон писал: Если в редкой среде, состоящей из равных частиц, свободно расположенных на равных расстояниях друг от друга, шар и цилиндр, описанные на одинаковом диаметре, движутся с равными скоростями в направлении оси цилиндра, сопротивление шара будет равным вдвое меньше, чем у цилиндра.

Следуя этому предложению, следует схолия, содержащая известное условие, что кривая, которая при вращении вокруг своей оси создает твердое тело, которое испытывает меньшее сопротивление, чем любое другое твердое тело, имеющее фиксированную длину и ширину.

В современной форме задача Ньютона состоит в том, чтобы минимизировать следующий интеграл:^[7][8]

${\displaystyle I=\int {\frac {y{\dot {y}}^{3}}{1+{\dot {y}}^{2}}}dx}$

куда ${\displaystyle y(x)}$ представляет собой кривую, образующую твердое тело при повороте вокруг оси x, а ${\displaystyle {\dot {y}}=dy/dx}$.

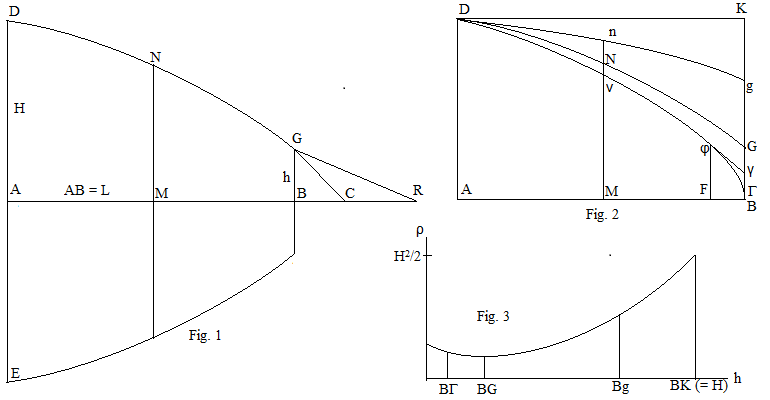
I - это уменьшение сопротивления, вызванное столкновением частиц с наклонной поверхностью DNG, образованной вращением кривой, а не перпендикулярно горизонтальной проекции DNG на задний диск DA от направления движения на рис. 1. Обратите внимание, что передняя часть твердого тела - это диск BG, треугольники GBC и GBR не являются его частью, но используются ниже Ньютоном для выражения условия минимума.

Этот интеграл связан с общим сопротивлением, которое испытывает тело, следующим соотношением: ${\displaystyle \rho ={\frac {H^{2}}{2}}+\int {\frac {y{\dot {y}}^{3}}{1+{\dot {y}}^{2}}}dx}$

Проблема состоит в том, чтобы найти кривую, которая создает твердое тело, которое испытывает меньшее сопротивление, чем любое другое твердое тело, имеющее фиксированную осевую длину = L и фиксированную ширину H.

Поскольку твердое тело должно сужаться в направлении движения, H - это радиус диска, образующего заднюю поверхность кривой, повернутой вокруг оси x. Единицы выбраны так, чтобы коэффициент пропорциональности был равен единице. Также обратите внимание, что ${\displaystyle {\dot {y}}<0}$, а интеграл, который вычисляется между x = 0 и x = L, отрицателен. Пусть y = h, когда x = L.

Когда кривая представляет собой горизонтальную линию, DK, поэтому твердое тело представляет собой цилиндр, ${\displaystyle y=H,{\dot {y}}=0}$, интеграл равен нулю, а сопротивление цилиндра равно: ${\displaystyle \rho ={\frac {H^{2}}{2}}}$, что объясняет постоянный член.

Условие минимального сопротивления твердого тела

Самый простой способ применить Уравнение Эйлера – Лагранжа. к этой проблеме стоит переписать сопротивление как:

${\displaystyle \rho ={\frac {H^{2}}{2}}+\int {\frac {y}{1+{\dot {x}}^{2}}}dy}$ куда ${\displaystyle {\dot {x}}=dx/dy}$, а интеграл, который вычисляется между y = H и y = h

Подставляя подынтегральное выражение ${\displaystyle F(y,{\dot {x}})=y/(1+{\dot {x}}^{2})}$ в уравнение Эйлера-Лагранжа

${\displaystyle {\frac {d}{dy}}\left({\frac {\partial F}{\partial {\dot {x}}}}\right)={\frac {d}{dy}}\left({\frac {-2{\dot {x}}y}{(1+{\dot {x}}^{2})^{2}}}\right)={\frac {\partial F}{\partial x}}=0}$, откуда следует, что ${\displaystyle {\frac {{\dot {x}}y}{(1+{\dot {x}}^{2})^{2}}}}$ постоянна, и это можно записать как

${\displaystyle y=K_{1}{\frac {(1+p^{2})^{2}}{p^{3}}}}$ (1) где ${\displaystyle p=-{\dot {y}}>0}$, и где ${\displaystyle K_{1}>0}$ является константой.

Хотя кривые, которые удовлетворяют условию минимума, не могут быть описаны простой функцией y = f (x), они могут быть построены с использованием p в качестве параметра для получения соответствующих координат (x, y) кривых. Уравнение x как функции p получается из условия минимума (1), и его эквивалент впервые был найден Ньютоном.

Различение: ${\displaystyle dy=-pdx=K_{1}(1-{\frac {2}{p^{2}}}-{\frac {3}{p^{4}}})dp}$, и интегрируя

${\displaystyle x=K_{2}-K_{1}\left(\ln p+{\frac {1}{p^{2}}}+{\frac {3}{4p^{4}}}\right)}$, куда ${\displaystyle K_{2}>0}$ является константой.

С ${\displaystyle y=H}$, когда ${\displaystyle x=0}$, и ${\displaystyle y=h}$, когда ${\displaystyle x=L}$, константы ${\displaystyle K_{1},\ K_{2}}$ может быть определен в терминах H, h и L. Поскольку y из уравнения (1) никогда не может быть нулевым или отрицательным, передняя поверхность любого твердого тела, удовлетворяющего условию минимума, должна быть диском GB.

Поскольку это был первый пример проблемы такого типа, Ньютону пришлось изобрести совершенно новый метод решения. Кроме того, в своем анализе проблемы он пошел гораздо глубже, чем просто нахождение условия (1).

Твердое наименьшее сопротивление

Хотя твердое тело наименьшего сопротивления должно удовлетворять (1), обратное неверно. На рис.2 показано семейство кривых, которые ему удовлетворяют для разных значений ${\displaystyle K_{1}>0}$. В качестве ${\displaystyle K_{1}}$ увеличивает радиус Bg = h диска при x = L, уменьшается и кривая становится круче.

Непосредственно перед проблемой минимального сопротивления Ньютон заявил, что если на любой эллиптической или овальной фигуре, вращающейся вокруг своей оси, p становится больше единицы, можно найти фигуру с меньшим сопротивлением. Это достигается заменой части твердого тела, имеющей p> 1, на усеченный конуса, угол при вершине которого является прямым углом, как показано на рис.2 для кривой ${\displaystyle D\nu \phi \gamma B}$. У этого меньше сопротивления, чем у ${\displaystyle D\nu \phi \Gamma B}$. Ньютон этого не доказывает, но добавляет, что он может найти применение в судостроении. Уайтсайд предоставляет доказательство и утверждает, что Ньютон использовал бы те же рассуждения.

На рис. 2, поскольку твердое тело, образованное кривой Dng, удовлетворяет условию минимума и имеет p <1 при g, оно испытывает меньшее сопротивление, чем сопротивление любой другой кривой с той же конечной точкой g. Однако для кривой DνΓ с p> 1 в конечной точке Γ это не так, поскольку, хотя кривая удовлетворяет условию минимума, сопротивление, которое испытывают вместе φγ и γΓ, меньше, чем сопротивление φΓ.

Ньютон пришел к выводу, что из всех твердых тел, удовлетворяющих условию минимального сопротивления, наименьшее сопротивление испытывает DNG на рис.2, которое имеет p = 1 при G. Это схематично показано на рис.3, где общее сопротивление твердое тело изменяется в зависимости от радиуса диска передней поверхности, минимум происходит при h = BG, что соответствует p = 1 при G.

В Принципах, на рис. 1 условие минимального сопротивления твердого тела переведено в геометрическую форму следующим образом: проведите ОТО параллельно касательной в точке N, так чтобы ${\displaystyle p={\frac {GB}{BR}}}$, и уравнение (1) принимает следующий вид: ${\displaystyle {\frac {NM.GB^{3}}{BR^{3}(1+(GB/BR)^{2})^{2}}}={\frac {NM.BR.GB^{3}}{GR^{4}}}=K_{1}}$

В G, ${\displaystyle NM=BG}$, ${\displaystyle BR=BC=BG}$, и ${\displaystyle GR^{2}=2BG^{2}}$, так ${\displaystyle {\frac {NM.BR.GB^{3}}{GR^{4}}}={\frac {GB}{4}}=K_{1}}$ который появляется в Principia в форме:

${\displaystyle {\frac {NM}{GR}}={\frac {GR^{3}}{4BR.GB^{2}}}}$

Вывод Ньютона условия минимального сопротивления

Хотя это кажется довольно простым, в нем есть несколько тонкостей, которые вызвали большую путаницу.

На рис.4 предположим, что DNSG - это кривая, которая при повороте вокруг AB образует твердое тело, сопротивление которого меньше, чем у любого другого такого твердого тела с такой же высотой, AD = H, BG = h и длиной, AB = L.

На рис. 5. более подробно показан бесконечно малый участок кривой вокруг N и I. Хотя NI, Nj и NJ действительно изогнуты, их можно аппроксимировать прямыми линиями, если NH достаточно мало.

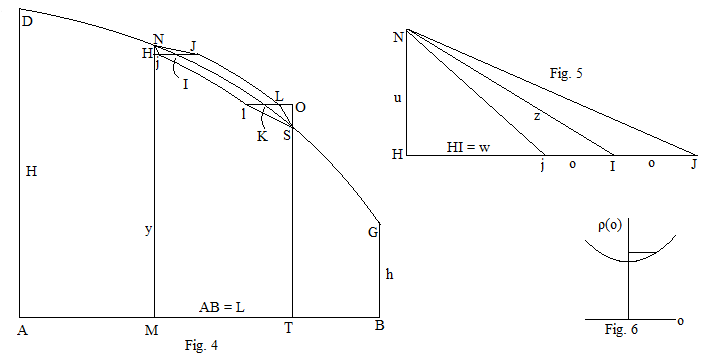
Пусть HM = y, AM = x, NH = u и HI = w = dx. Пусть касательная в каждой точке кривой, ${\displaystyle p=-{\frac {dy}{dx}}={\frac {u}{w}}}$. Уменьшение сопротивления наклонного кольца NI по сравнению с вертикальным кольцом NH, повернутым вокруг AB, составляет ${\displaystyle r={\frac {yp^{3}}{1+p^{2}}}dx={\frac {yu^{3}}{u^{2}+w^{2}}}}$ (2)

Пусть твердое тело минимального сопротивления заменено идентичным, за исключением того, что дуга между точками I и K сдвинута на небольшое расстояние вправо ${\displaystyle IJ=KL=o>0}$, или влево ${\displaystyle Ij=Kl=o<0}$, как более подробно показано на рис. 5. В любом случае HI становится ${\displaystyle HJ,Hj=w+o}$.

Сопротивления дуг кривой DN и SG неизменны. Также сопротивление дуги IK не изменяется при смещении, так как наклон остается неизменным по ее длине. Единственное изменение общего сопротивления DNSG связано с изменением градиента дуг NI и KS. Два смещения должны быть равными, чтобы угол наклона дуги IK не изменился, а новая кривая оканчивалась в точке G.

Новое сопротивление из-за столкновения частиц с NJ или Nj, а не с NI, равно:

${\displaystyle r+\delta r={\frac {yu^{3}}{u^{2}+(w+o)^{2}}}=r-{\frac {2ywu^{3}o}{(u^{2}+w^{2})^{2}}}}$ + w. (в возрастающих степенях ${\displaystyle {\frac {o}{w}}}$ начиная со 2-го).

В результате изменяется сопротивление: ${\displaystyle -{\frac {2NM.HI.HN^{3}o}{NI^{4}}}}$ + члены более высокого порядка, сопротивление уменьшается, если o> 0 (сопротивление NJ меньше, чем сопротивление NI).

Это первоначальный вывод 1685 года, в котором он получил вышеуказанный результат, используя разложение в ряд по степеням o. В своем повторном посещении 1694 года он дифференцирует (2) по w. Он отправил подробности своего более позднего подхода Дэвиду Грегори, и они включены в качестве приложения в перевод «Начала» Мотта.

Точно так же изменение сопротивления из-за столкновения частиц с SL или Sl, а не с SK, равно: ${\displaystyle +{\frac {2TS.OK.OS^{3}o}{SK^{4}}}}$ + условия более высокого порядка.

Общее изменение сопротивления всего твердого тела, ${\displaystyle \delta \rho =(-{\frac {2NM.HI.HN^{3}}{NI^{4}}}+{\frac {2TS.OK.OS^{3}}{SK^{4}}})o}$ + w. (в возрастающих степенях ${\displaystyle {\frac {o}{w}}}$ начиная со 2-го).

На рис. 6 показано полное сопротивление DNJLSG или DNJLSG в зависимости от o. Поскольку исходная кривая DNIKSG имеет наименьшее сопротивление, любое изменение любого знака должно приводить к увеличению сопротивления. Это возможно только в том случае, если коэффициент при разложении ${\displaystyle \rho (o)}$ равно нулю, поэтому:

${\displaystyle {\frac {NM.HI.HN^{3}}{NI^{4}}}={\frac {TS.OK.OS^{3}}{SK^{4}}}}$ (2)

Если бы это было не так, можно было бы выбрать значение o со знаком, который дает кривую DNJLSG, или DNjlSG с меньшим сопротивлением, чем исходная кривая, вопреки исходному предположению. Аппроксимация прямых линий для конечных дуг, NI и KS становится точной в пределе, когда HN и OS приближаются к нулю. Кроме того, NM и HM можно считать равными, как и OT и ST.

Однако N и S на исходной кривой являются произвольными точками, поэтому для любых двух точек в любом месте кривой должно применяться указанное выше равенство. Это возможно только в том случае, если в пределах любой бесконечно малой дуги HI в любом месте кривой выражение

${\displaystyle {\frac {NM.HI.HN^{3}}{NI^{4}}}}$ является константой. (3)

Это должно быть так, поскольку, если ${\displaystyle {\frac {NM.HI.HN^{3}}{NI^{4}}}}$ должно было меняться вдоль кривой, можно было бы найти 2 бесконечно малые дуги NI и KS, такие, что (2) было ложным, и коэффициент при разложении ${\displaystyle \delta \rho }$ будет ненулевым. Тогда можно получить твердое тело с меньшим сопротивлением, выбрав подходящее значение o.

Это причина постоянного члена в условии минимума в (3). Как отмечалось выше, Ньютон пошел дальше и заявил, что сопротивление твердого тела меньше, чем у любого другого твердого тела той же длины и ширины, когда наклон в точке G равен единице. Следовательно, в этом случае постоянная в (3) равна одной четверти радиуса переднего диска твердого тела, ${\displaystyle {\frac {GB}{4}}}$.

Рекомендации

1. Ньютон, Исаак. «Philosophiæ Naturalis Principia Mathematica (Математические принципы естественной философии)». Лондон (1687 г.) (1987 г.).
2. Голдстайн, Герман Гейне. История вариационного исчисления с 17 по 19 век. Vol. 5. Springer Science & Business Media, 2012.
3. Newton, I. «Philosophi Naturalis Principia Mathematica, перевод» А. Мотта (1729 г.), переработанный Ф. Каджори (1934 г.) »Беркли, Калифорния: University of California Press 140: 175.
4. Коэн, И. Бернард; Уитмен, Энн (1999). Принципы, Новый перевод. Калифорнийский университет Press. п. 182.
5. Уайтсайд, Д. Т. (1974). Математические статьи Исаака Ньютона, том 6. Издательство Кембриджского университета. С. 456, 470–480.
6. Хейс, В. Д., Пробштейн, Р. Ф. (1967). Теория гиперзвукового потока: Невязкие потоки. Академическая пресса.
7. Чандрасекар, Субраманян. Начала Ньютона для обычного читателя. Издательство Оксфордского университета, 1995.
8. Дэвис, Гарольд Тайер. Введение в нелинейные дифференциальные и интегральные уравнения. Курьерская корпорация, 1962 год.