Модель популяции - Population model

А модель населения это тип математическая модель что применяется к изучению динамика населения.

Обоснование

Модели позволяют лучше понять, как работают сложные взаимодействия и процессы. Моделирование динамических взаимодействий в природе может обеспечить управляемый способ понять, как числа меняются со временем или по отношению друг к другу. Многие закономерности можно заметить, используя моделирование населения в качестве инструмента.^[1]

Экологический Моделирование популяции связано с изменениями таких параметров, как численность населения и возрастное распределение внутри населения. Это может быть связано с взаимодействием с окружающей средой, представителями своего вида или другими видами.^[2]

Популяционные модели используются для определения максимального урожая для агрономов, чтобы понять динамику биологические инвазии, и для охрана окружающей среды. Модели популяций также используются для понимания распространения паразитов, вирусов и болезнь.^[2]

Еще один способ использования популяционных моделей - это когда виды находятся под угрозой исчезновения. Модели популяций могут отслеживать хрупкие виды и работать и сдерживать сокращение. [1]

История

В конце 18 века биологи начали разрабатывать методы моделирования популяций, чтобы понять динамику роста и сокращения всех популяций живых организмов. Томас Мальтус был одним из первых, кто заметил, что популяции росли по геометрической схеме, размышляя о судьбе человечества.^[3] Одной из самых основных и важных моделей роста населения была логистическая модель роста населения сформулировано Пьер Франсуа Верхюльст в 1838 году. Логистическая модель принимает форму сигмовидная кривая и описывает рост населения как экспоненциальный, за которым следует снижение прироста, и ограниченный пропускной способностью из-за давления окружающей среды.^[4]

Моделирование популяций стало особенно интересным для биологов в 20-м веке, поскольку давление на ограниченные средства к существованию из-за увеличения человеческого населения в некоторых частях Европы было замечено такими биологами, как Раймонд Перл. В 1921 году Перл пригласил физика. Альфред Дж. Лотка чтобы помочь ему в его лаборатории. Лотка разработала парную дифференциальные уравнения это показало действие паразита на свою жертву. Математик Вито Вольтерра приравнял отношения между двумя видами, независимыми от Лотки. Вместе Лотка и Вольтерра сформировали Модель Лотки – Вольтерры для конкуренции, которая применяет логистическое уравнение к двум видам, иллюстрируя взаимодействия между видами конкуренции, хищничества и паразитизма.^[3] В 1939 году вклад в популяционное моделирование был внесен Патриком Лесли, когда он начал работать в области биоматематики. Лесли подчеркнул важность построения таблицы дожития, чтобы понять влияние ключевых стратегий жизненного цикла на динамику всего населения. Матричная алгебра использовалась Лесли в сочетании с таблицами дожития, чтобы расширить работу Лотки.^[5] Матричные модели численности населения рассчитывают рост населения с переменными жизненного цикла. Потом, Роберт Макартур и Э. О. Уилсон охарактеризована биогеография острова. В равновесная модель островной биогеографии описывает количество видов на острове как равновесие иммиграции и исчезновения. Логистическая модель популяции, модель экологии сообщества Лотки – Вольтерры, матричное моделирование таблицы дожития, равновесная модель островной биогеографии и ее вариации являются сегодня основой экологического моделирования популяций.^[6]

Уравнения

Логистический рост уравнение:

${displaystyle {frac {dN}{dt}}=rNleft(1-{frac {N}{K}}ight),}$

Уравнение Лотки – Вольтерра:

${displaystyle {frac {dN_{1}}{dt}}=r_{1}N_{1}{frac {K_{1}-N_{1}-alpha N_{2}}{K_{1}}},}$

Биогеография острова:

${displaystyle S={frac {IP}{I+E}}}$

Взаимосвязь видов и ареалов:

${displaystyle log(S)=log(c)+zlog(A),}$

Примеры индивидуальных моделей

Логический детерминированный индивидуальный подход клеточные автоматы модель экосистемы с одним видом. Модель демонстрирует механизм S-образного роста населения.

Логическая детерминированная индивидуально-ориентированная клеточно-автоматная модель межвидовой конкуренции за единственный ограниченный ресурс. Механизм конкурентного исключения одного вида другим.

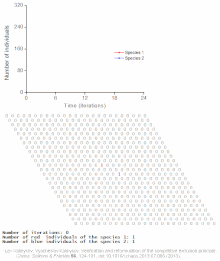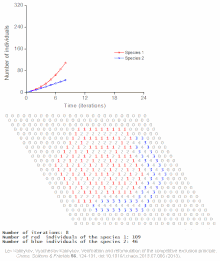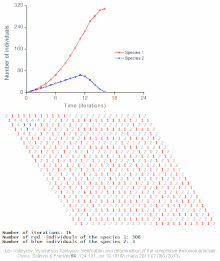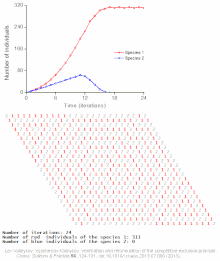
Смотрите также

• Динамика населения
• Динамика численности рыбного промысла
• Экология населения
• Момент закрытия

Рекомендации

1. Уорстер, Дональд (1994). Экономика природы. Издательство Кембриджского университета. С. 398–401.
2. Уенояма, Марси (2004). Рама Сингх (ред.). Эволюция популяционной биологии. Издательство Кембриджского университета. С. 1–19.
3. Макинтош, Роберт (1985). Предпосылки экологии. Издательство Кембриджского университета. С. 171–198.
4. Реншоу, Эрик (1991). Моделирование биологических популяций в пространстве и времени. Издательство Кембриджского университета. С. 6–9.
5. Кингсленд, Шарон (1995). Моделирование природы: эпизоды истории популяционной экологии. Издательство Чикагского университета. С. 127–146.
6. Готелли, Николай (2001). Букварь по экологии. Синауэр.

внешняя ссылка

• Сеть обмена кодами GreenBoxes. Greenboxes (Beta) - это репозиторий для открытого кода моделирования населения. Greenboxes позволяет пользователям легко делиться своим кодом и искать общий код других пользователей.