Стратегическое господство - Strategic dominance

Для бизнес-стратегии см. Доминирование (экономика).

В теория игры, стратегическое превосходство (обычно называют просто господство) происходит, когда один стратегия лучше, чем другая стратегия для одного игрока, независимо от того, как могут играть оппоненты этого игрока. Многие простые игры можно решить, используя доминирование. Противоположный, непроницаемость, происходит в играх, где одна стратегия может быть лучше или хуже другой стратегии для одного игрока, в зависимости от того, как могут играть противники игрока.

Терминология

Когда игрок пытается выбрать «лучшую» стратегию среди множества вариантов, этот игрок может сравнить две стратегии A и B, чтобы увидеть, какая из них лучше. Результатом сравнения является один из:

• B эквивалентно A: выбор B всегда дает тот же результат, что и выбор A, независимо от того, что делают другие игроки.
• B строго доминирует A: выбор B всегда дает лучший результат, чем выбор A, независимо от того, что делают другие игроки.
• B слабо доминирует A: выбор B всегда дает по крайней мере такой же хороший результат, как выбор A, независимо от того, что делают другие игроки, и есть по крайней мере один набор действий оппонентов, для которых B дает лучший результат, чем A. (Обратите внимание, что если B строго доминирует над A, тогда B слабо доминирует над A. Следовательно, мы можем сказать «B доминирует над A» как синоним «B слабо доминирует над A».)^[1]
• B и A являются непереходный: B и A не эквивалентны, и B не доминирует и не подчиняется A. Выбор A в некоторых случаях лучше, в то время как выбор B лучше в других случаях, в зависимости от того, как именно оппонент решает играть. Например, B - это «бросать камень», а A - «бросать ножницы» в Камень ножницы Бумага.
• B - это слабо доминируемый на A: есть по крайней мере один набор действий оппонентов, для которых B дает худший результат, чем A, в то время как все другие наборы действий оппонентов дают A такой же выигрыш, как и B. (Стратегия A слабо доминирует над B).
• B - это строго доминируют от A: выбор B всегда дает худший результат, чем выбор A, независимо от того, что делают другие игроки. (Стратегия A строго доминирует над B).

Это понятие можно обобщить, не сравнивая две стратегии.

• Стратегия B строго доминирующий если стратегия B строго доминирует любая другая возможная стратегия.
• Стратегия B слабо доминирующий если стратегия B доминирует все другие стратегии, но некоторые (или все) стратегии только слабо доминируемый автор Б.
• Стратегия B строго доминируют если существует другая стратегия, строго доминирующая над B.
• Стратегия B слабо доминируемый если существует другая стратегия, слабо доминирующая над B.

Стратегия: Полный случайный план для игрока в игре. Полный непредвиденный план - это полная спецификация поведения игрока, описывающая каждое действие, которое игрок предпримет на каждой возможной точке принятия решения. Поскольку информационные наборы представляют собой точки в игре, где игрок должен принять решение, стратегия игрока описывает, что этот игрок будет делать с каждым информационным набором.^[2]

Рациональность: Предположение о том, что каждый игрок действует таким образом, чтобы добиться того, что он или она больше всего предпочитает, с учетом вероятностей различных исходов; фон Нейман и Моргенштерн показали, что если эти предпочтения удовлетворяют определенным условиям, это математически эквивалентно максимизации выигрыша. Простой пример максимизации выигрыша - это денежная выгода, но для целей анализа теории игр этот выигрыш может принимать любую форму. Будь то денежное вознаграждение, минимизация усилий или дискомфорта, продвижение справедливости, распространение собственных генов или накопление общей «полезности» - предположение о рациональности утверждает, что игроки всегда будут действовать таким образом, который наилучшим образом удовлетворяет их порядок от лучшего к худшему из различных возможные исходы.^[2]

Всем известный факт: Предположение, что каждый игрок знает игру, знает правила и выплаты, связанные с каждым курсом действий, и понимает, что каждый другой игрок имеет такой же уровень понимания. Это предпосылка, которая позволяет игроку делать оценочное суждение о действиях другого игрока, подкрепленное предположением о рациональности, с учетом при выборе действия.^[2]

Доминирование и равновесие по Нэшу

	C	D
C	1, 1	0, 0
D	0, 0	0, 0

Если для одного игрока в игре существует строго доминирующая стратегия, этот игрок будет использовать эту стратегию в каждой игре. Равновесия Нэша. Если у обоих игроков есть строго доминирующая стратегия, в игре будет только одно уникальное равновесие по Нэшу. Однако это равновесие по Нэшу не обязательно является «эффективным», а это означает, что могут быть неравновесные исходы игры, которые были бы лучше для обоих игроков. Классическая игра, используемая для иллюстрации этого, - Дилемма заключенного.

Строго доминируемые стратегии не могут быть частью равновесия по Нэшу, и поэтому для любого игрока нерационально их использовать. С другой стороны, стратегии со слабым доминированием могут быть частью равновесия по Нэшу. Например, рассмотрим матрица выплат на фото справа.

Стратегия C слабо доминирует над стратегией Д. Подумайте об игре C: Если противник играет C, один получает 1; если противник играет D, один получает 0. Сравните это с D, где каждый получает 0 независимо. Так как в одном случае лучше, играя C вместо того D и никогда не бывает хуже, C слабо доминирует D. Несмотря на это, ${\displaystyle (D,D)}$ является равновесием по Нэшу. Предположим, оба игрока выбирают D. Ни один из игроков не добьется большего, если в одностороннем порядке отклонится - если игрок переключится на игру C, они по-прежнему будут иметь 0. Это удовлетворяет требованиям равновесия по Нэшу. Предположим, оба игрока выбирают C. Ни один из игроков не добьется большего, если в одностороннем порядке отклонится - если игрок переключится на игру D, он получит 0. Это также удовлетворяет требованиям равновесия по Нэшу.

Итеративное исключение строго доминируемых стратегий (IESDS)

Повторное исключение (или удаление) доминируемых стратегий (также называемых IESDS или IDSDS) является одним из распространенных методов решения игр, которые включают итеративно удаление доминирующих стратегий. На первом этапе не более одной доминируемой стратегии удаляется из пространства стратегий каждого из игроков, поскольку ни один рациональный игрок никогда не будет использовать эти стратегии. Это приводит к новой, меньшей игре. Некоторые стратегии, в которых раньше не было доминирования, могут доминировать в более мелкой игре. Первый шаг повторяется, создается новая игра еще меньшего размера и так далее. Процесс останавливается, когда ни один из игроков не находит доминирующей стратегии. Этот процесс действителен, поскольку предполагается, что рациональность среди игроков всем известный факт, то есть каждый игрок знает, что остальные игроки рациональны, и каждый игрок знает, что остальные игроки знают, что он знает, что остальные игроки рациональны, и так далее до бесконечности (см. Aumann, 1976). .

Есть две версии этого процесса. Одна версия предполагает только устранение строго доминируемых стратегий. Если после завершения этого процесса остается только одна стратегия для каждого игрока, этот набор стратегий является уникальным равновесием по Нэшу.^[3]

Пошаговый пример строгого удаления доминирования:

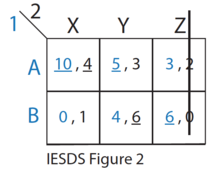
1. В C строго доминирует A для Игрока 1. Следовательно, Игрок 1 никогда не будет играть в стратегию C. Игрок 2 это знает. (см. рисунок 1 IESDS)
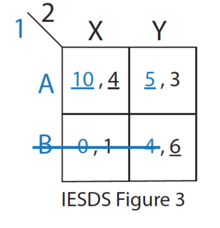
2. Из остальных стратегий (см. Рис. 2 IESDS) в Z строго доминируют Y и X для Игрока 2. Следовательно, Игрок 2 никогда не будет играть в стратегию Z. Игрок 1 это знает.
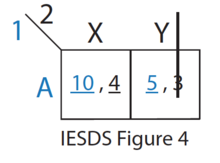
3. Из остальных стратегий (см. Рисунок 3 IESDS) в B строго доминирует A для игрока 1. Следовательно, игрок 1 никогда не будет играть B. Игрок 2 это знает.
4. Из остальных стратегий (см. Рис. 4 IESDS) в Y строго доминирует X для Игрока 2. Следовательно, Игрок 2 никогда не будет играть Y. Игрок 1 это знает.
5. Остается только одна рационализируемая стратегия {A, X}, результатом которой является выигрыш (10,4). Это единственное равновесие по Нэшу в этой игре.

Другой вариант предполагает устранение как строго, так и слабо доминируемых стратегий. Если в конце процесса для каждого игрока существует одна стратегия, этот набор стратегий также является равновесие по Нэшу. Однако, в отличие от первого процесса, устранение слабо доминируемых стратегий может устранить некоторые равновесия по Нэшу. В результате равновесие по Нэшу, найденное путем исключения слабо доминируемых стратегий, может не быть только Равновесие по Нэшу. (В некоторых играх, если мы удалим стратегии со слабым доминированием в другом порядке, мы можем получить другое равновесие по Нэшу.)

Пошаговый пример удаления слабого доминирования:

1. O строго доминирует N для игрока 1. Следовательно, игрок 1 никогда не будет играть стратегию O. Игрок 2 знает это. (см. рисунок 5 IESDS)
2. U слабо доминирует над T для Игрока 2. Если Игрок 2 выбирает T, то окончательное равновесие будет (N, T)

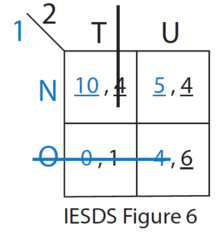
1. O строго доминирует N для игрока 1. Следовательно, игрок 1 никогда не будет играть стратегию O. Игрок 2 знает это. (см. рисунок 6 IESDS)
2. В T слабо доминирует U для Игрока 2. Если Игрок 2 выбирает U, то окончательное равновесие будет (N, U)

В любом случае, если при повторном исключении доминируемых стратегий остается только одна стратегия для каждого игрока, игра называется разрешимый игра.

Смотрите также

• Арбитраж
• Стратегия, в которой доминирует Макс
• Парадокс Ньюкомба
• Доминирование риска
• Стратегия победы

использованная литература

1. Лейтон-Браун, Кевин; Шохам, Йоав (январь 2008 г.). «Основы теории игр: краткое междисциплинарное введение». Синтез лекций по искусственному интеллекту и машинному обучению. 2 (1): 36. Дои:10.2200 / S00108ED1V01Y200802AIM003.
2. Джоэл., Ватсон (09.05.2013). Стратегия: введение в теорию игр (Третье изд.). Нью-Йорк. ISBN  9780393918380. OCLC  842323069.
3. Joel., Watson ,. Стратегия: введение в теорию игр (Второе изд.). Нью-Йорк. ISBN  9780393929348.

• Фуденберг, Дрю; Тироль, Жан (1993). Теория игры. MIT Press.
• Гиббонс, Роберт (1992). Теория игр для экономистов-прикладников. Издательство Принстонского университета. ISBN  0-691-00395-5.
• Гиниц, Герберт (2000). Развитие теории игр. Издательство Принстонского университета. ISBN  0-691-00943-0.
• Лейтон-Браун, Кевин; Шохам, Йоав (2008). Основы теории игр: краткое междисциплинарное введение. Сан-Рафаэль, Калифорния: Издательство Morgan & Claypool. ISBN  978-1-59829-593-1.. 88-страничное математическое введение; см. раздел 3.3. Бесплатно онлайн во многих университетах.
• Рапопорт, А. (1966). Теория игр для двух лиц: основные идеи. Пресса Мичиганского университета.
• Курс Джима Рэтлиффа по теории игр: стратегическое превосходство
• Шохам, Йоав; Лейтон-Браун, Кевин (2009). Мультиагентные системы: алгоритмические, теоретико-игровые и логические основы. Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-89943-7.. Исчерпывающий справочник с вычислительной точки зрения; см. разделы 3.4.3, 4.5. Скачать бесплатно онлайн.

В эту статью вошли материалы из стратегии Dominant PlanetMath, который находится под лицензией Лицензия Creative Commons Attribution / Share-Alike.