Биполярные цилиндрические координаты - Bipolar cylindrical coordinates - Wikipedia

Координатные поверхности биполярных цилиндрических координат. Желтый полумесяц соответствует σ, тогда как красная трубка соответствует τ, а синяя плоскость соответствует z= 1. Три поверхности пересекаются в точке п (показан черной сферой).

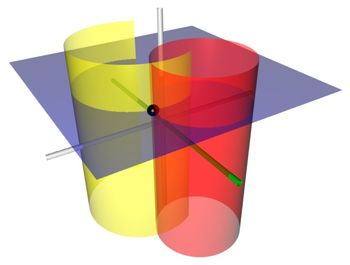
Биполярные цилиндрические координаты являются трехмерными ортогональный система координат который возникает в результате проецирования двухмерного биполярная система координат в перпендикулярном ${\displaystyle z}$-направление. Две строки фокусы ${\displaystyle F_{1}}$ и ${\displaystyle F_{2}}$ проектируемых Аполлонические круги обычно считаются определяемыми ${\displaystyle x=-a}$ и ${\displaystyle x=+a}$соответственно (и ${\displaystyle y=0}$) в Декартова система координат.

Термин «биполярный» часто используется для описания других кривых, имеющих две особые точки (фокусы), таких как эллипсы, гиперболы, и Кассини овалы. Однако срок биполярные координаты никогда не используется для описания координат, связанных с этими кривыми, например, эллиптические координаты.

Основное определение

Наиболее распространенное определение биполярных цилиндрических координат ${\displaystyle (\sigma ,\tau ,z)}$ является

${\displaystyle x=a\ {\frac {\sinh \tau }{\cosh \tau -\cos \sigma }}}$

${\displaystyle y=a\ {\frac {\sin \sigma }{\cosh \tau -\cos \sigma }}}$

${\displaystyle z=\ z}$

где ${\displaystyle \sigma }$ координата точки ${\displaystyle P}$равен углу ${\displaystyle F_{1}PF_{2}}$ и ${\displaystyle \tau }$ координата равна натуральный логарифм отношения расстояний ${\displaystyle d_{1}}$ и ${\displaystyle d_{2}}$ к фокусным линиям

${\displaystyle \tau =\ln {\frac {d_{1}}{d_{2}}}}$

(Напомним, что фокусные линии ${\displaystyle F_{1}}$ и ${\displaystyle F_{2}}$ расположены в ${\displaystyle x=-a}$ и ${\displaystyle x=+a}$, соответственно.)

Поверхности постоянного ${\displaystyle \sigma }$ соответствуют цилиндрам разного радиуса

${\displaystyle x^{2}+\left(y-a\cot \sigma \right)^{2}={\frac {a^{2}}{\sin ^{2}\sigma }}}$

все они проходят через фокальные линии и не являются концентрическими. Поверхности постоянного ${\displaystyle \tau }$ представляют собой непересекающиеся цилиндры разного радиуса

${\displaystyle y^{2}+\left(x-a\coth \tau \right)^{2}={\frac {a^{2}}{\sinh ^{2}\tau }}}$

которые окружают фокальные линии, но опять же не концентрические. Фокальные линии и все эти цилиндры параллельны ${\displaystyle z}$-ось (направление проецирования). в ${\displaystyle z=0}$ плоскости, центры постоянных-${\displaystyle \sigma }$ и постоянно-${\displaystyle \tau }$ баллоны лежат на ${\displaystyle y}$ и ${\displaystyle x}$ оси соответственно.

Коэффициенты масштабирования

Масштабные коэффициенты для биполярных координат ${\displaystyle \sigma }$ и ${\displaystyle \tau }$ равны

${\displaystyle h_{\sigma }=h_{\tau }={\frac {a}{\cosh \tau -\cos \sigma }}}$

тогда как оставшийся коэффициент масштабирования ${\displaystyle h_{z}=1}$. Таким образом, бесконечно малый элемент объема равен

${\displaystyle dV={\frac {a^{2}}{\left(\cosh \tau -\cos \sigma \right)^{2}}}d\sigma d\tau dz}$

а лапласиан равен

${\displaystyle \nabla ^{2}\Phi ={\frac {1}{a^{2}}}\left(\cosh \tau -\cos \sigma \right)^{2}\left({\frac {\partial ^{2}\Phi }{\partial \sigma ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \tau ^{2}}}\right)+{\frac {\partial ^{2}\Phi }{\partial z^{2}}}}$

Другие дифференциальные операторы, такие как ${\displaystyle \nabla \cdot \mathbf {F} }$ и ${\displaystyle \nabla \times \mathbf {F} }$ можно выразить в координатах ${\displaystyle (\sigma ,\tau )}$ подставив масштабные коэффициенты в общие формулы, найденные в ортогональные координаты.

Приложения

Классические приложения биполярных координат заключаются в решении уравнения в частных производных, например, Уравнение Лапласа или Уравнение Гельмгольца, для которых биполярные координаты позволяют разделение переменных (в 2D). Типичным примером может служить электрическое поле окружающие два параллельных цилиндрических проводника.

Библиография

• Margenau H, Мерфи GM (1956). Математика физики и химии. Нью-Йорк: Д. ван Ностранд. стр.187 –190. LCCN  55010911.
• Корн Г.А., Корн Т.М. (1961). Математический справочник для ученых и инженеров. Нью-Йорк: Макгроу-Хилл. п. 182. LCCN  59014456. ASIN B0000CKZX7.
• Мун П., Спенсер Д.Е. (1988). «Конические координаты (r, θ, λ)». Справочник по теории поля, включая системы координат, дифференциальные уравнения и их решения (исправленное 2-е изд., 3-е изд.). Нью-Йорк: Springer-Verlag. неизвестный. ISBN  978-0-387-18430-2.

внешняя ссылка

• MathWorld описание биполярных цилиндрических координат